0.8 Percent As A Fraction
zacarellano
Sep 15, 2025 · 5 min read
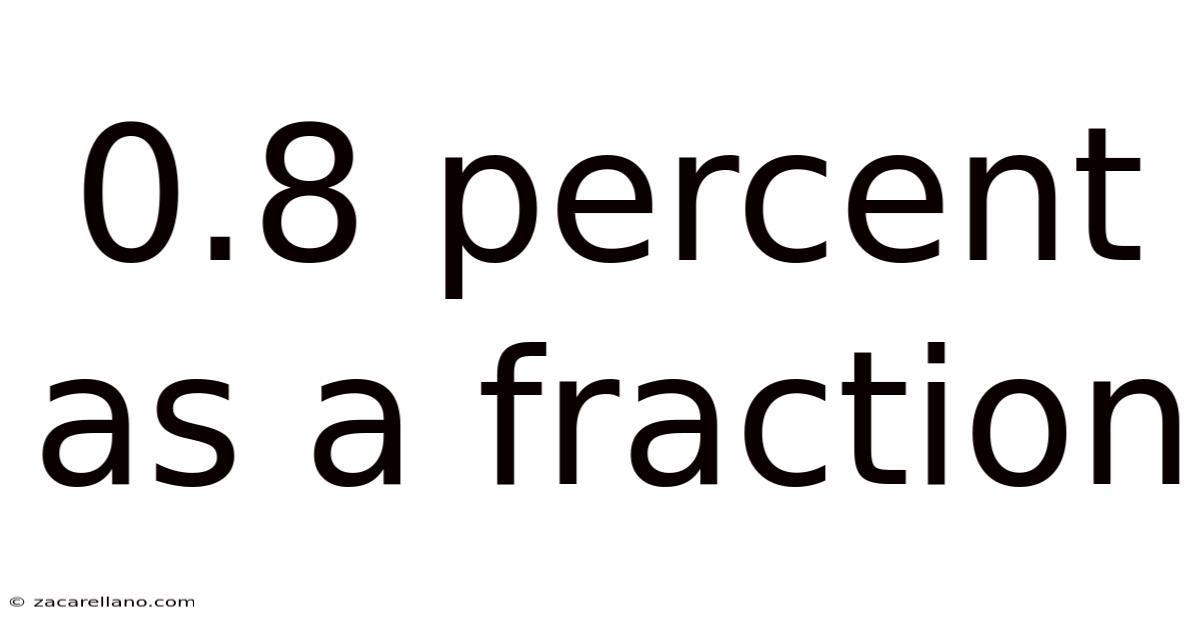
Table of Contents
Understanding 0.8 Percent as a Fraction: A Comprehensive Guide
Introduction:
Many find working with percentages and fractions challenging, but understanding the relationship between them is crucial for various applications, from everyday calculations to advanced mathematics. This article provides a comprehensive guide on converting 0.8 percent into a fraction, explaining the process step-by-step and exploring the underlying concepts. We'll delve into the meaning of percentages and fractions, offer multiple methods for the conversion, and address frequently asked questions. By the end, you'll not only know the fractional equivalent of 0.8 percent but also grasp the broader principles involved. This guide is designed for students, educators, and anyone seeking to strengthen their understanding of mathematical concepts.
Understanding Percentages and Fractions
Before diving into the conversion, let's refresh our understanding of percentages and fractions.
-
Percentage: A percentage represents a fraction of 100. The term "percent" literally means "out of one hundred" ( per cent). For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100.
-
Fraction: A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of parts, while the numerator indicates how many of those parts are being considered. For example, the fraction 1/4 represents one part out of four equal parts.
Converting 0.8 Percent to a Fraction: Step-by-Step
There are several ways to convert 0.8 percent into a fraction. Let's explore two common methods:
Method 1: Direct Conversion
-
Write 0.8% as a decimal: The percent symbol (%) means "divided by 100". Therefore, 0.8% can be written as 0.8 / 100.
-
Convert the decimal to a fraction: The decimal 0.8 can be written as 8/10. Therefore, our expression becomes (8/10) / 100.
-
Simplify the complex fraction: To simplify a complex fraction (a fraction within a fraction), multiply the numerator by the reciprocal of the denominator. The reciprocal of 100 is 1/100. So we get: (8/10) * (1/100) = 8/1000.
-
Simplify the fraction: Both 8 and 1000 are divisible by 8. Dividing both the numerator and denominator by 8, we get: 1/125.
Therefore, 0.8% is equal to 1/125.
Method 2: Using the Percentage as a Decimal Directly
-
Convert the percentage to a decimal: Divide 0.8 by 100: 0.8 / 100 = 0.008
-
Convert the decimal to a fraction: The decimal 0.008 can be written as 8/1000.
-
Simplify the fraction: Divide both the numerator and denominator by their greatest common divisor, which is 8: 8/1000 = 1/125.
Again, we arrive at the simplified fraction 1/125.
Visualizing the Fraction
Imagine a pizza cut into 125 equal slices. 0.8% represents just one of those slices. This visualization helps to understand the relatively small magnitude of 0.8%.
Different Approaches and Considerations
While the methods above are straightforward, it's important to note that depending on the context, alternative approaches might be necessary. For instance, if you were working with a larger percentage, you might need to employ techniques involving prime factorization to simplify the resulting fraction effectively. Similarly, if you encounter recurring decimals, the conversion process might involve slightly different steps, often resulting in fractions with repeating decimals in the numerator or denominator.
Scientific and Practical Applications
Understanding the conversion between percentages and fractions is crucial in several scientific and practical applications. Consider these examples:
-
Chemistry: Concentration of solutions is often expressed as a percentage or a fraction. Converting between these forms allows for consistent calculations and comparisons.
-
Finance: Interest rates, discounts, and tax calculations frequently involve percentages. Understanding their fractional equivalents aids in accurate financial computations.
-
Statistics: Data representation and analysis often involve proportions and ratios, which are closely related to fractions and percentages.
-
Engineering: Calculations involving tolerances, proportions, and scaling in design and manufacturing frequently utilize fractions and percentages.
Frequently Asked Questions (FAQ)
-
Q: Can 0.8% be expressed as a decimal?
- A: Yes, 0.8% is equivalent to 0.008 as a decimal.
-
Q: Is there only one way to represent 0.8% as a fraction?
- A: While 1/125 is the simplest form, technically, any equivalent fraction (e.g., 2/250, 3/375, etc.) also represents 0.8%. However, the simplest form is always preferred for clarity and ease of calculation.
-
Q: What if the percentage is a larger number, like 12.5%?
- A: The same principles apply. You would convert 12.5% to 12.5/100 = 0.125 = 125/1000, then simplify to 1/8.
-
Q: How do I convert a fraction back to a percentage?
- A: To convert a fraction to a percentage, divide the numerator by the denominator and multiply the result by 100. For example, 1/125 = 0.008 * 100 = 0.8%.
-
Q: Why is simplifying fractions important?
- A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It presents the most concise and efficient representation of the value.
Conclusion:
Converting 0.8% to a fraction (1/125) may seem like a simple task, but it underscores the fundamental relationship between percentages and fractions. Mastering this conversion is essential for various mathematical and real-world applications. By understanding the underlying principles and practicing the different methods, you'll gain confidence in handling percentages and fractions, enhancing your mathematical proficiency. This knowledge will be beneficial whether you're tackling academic challenges or solving everyday problems involving proportions and ratios. Remember to always simplify your fractions to their lowest terms for the clearest and most efficient representation of the value.
Latest Posts
Latest Posts
-
The Simplest Form Of Matter
Sep 15, 2025
-
How To Graph Reciprocal Functions
Sep 15, 2025
-
Religious Groups In Chesapeake Colonies
Sep 15, 2025
-
Lcm For 3 And 6
Sep 15, 2025
-
What Is Period Of Oscillation
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 0.8 Percent As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.