0 X 2 2x 1
zacarellano
Sep 23, 2025 · 6 min read
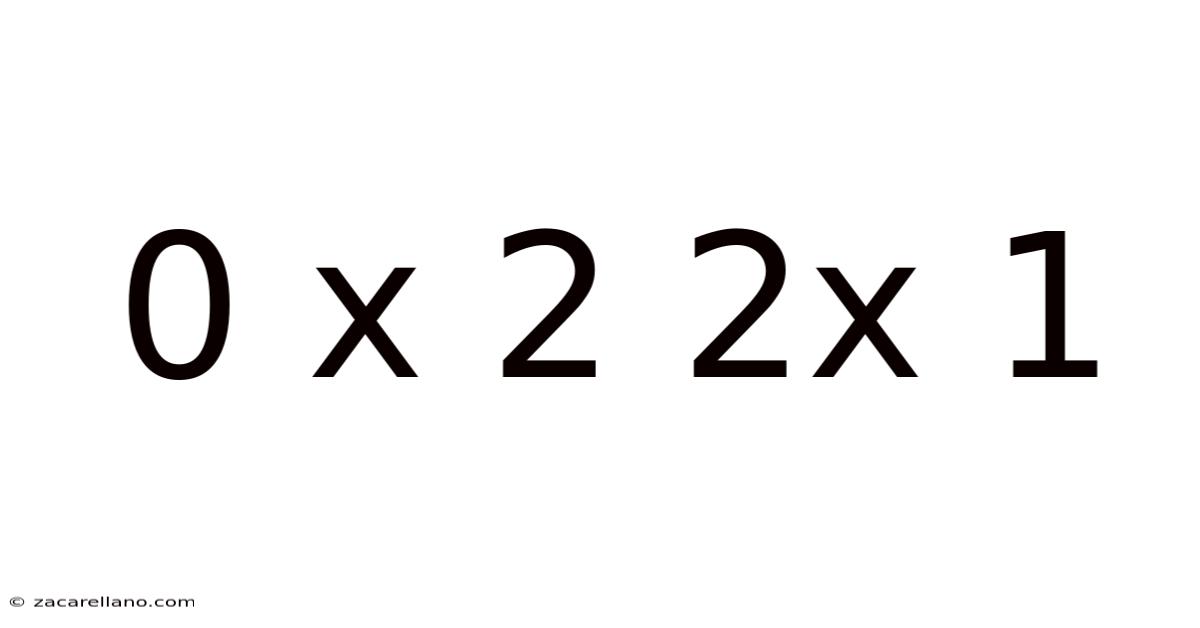
Table of Contents
Decoding the Enigma: A Deep Dive into 0 x 2, 2 x 1, and the Fundamentals of Multiplication
This article explores the seemingly simple yet fundamentally important mathematical concepts embodied in the expressions "0 x 2" and "2 x 1." While these calculations might appear trivial at first glance, they serve as crucial building blocks for understanding more complex mathematical operations and the underlying principles of arithmetic. We will delve into the properties of zero, the concept of multiplication itself, and the practical applications of these seemingly basic equations. This exploration will be accessible to learners of all levels, from elementary school students to those seeking a refresher on fundamental mathematical concepts.
Introduction: The Power of the Basics
Mathematics, at its core, is a system built upon fundamental principles. Understanding these principles is paramount to mastering more advanced topics. The expressions "0 x 2" and "2 x 1," while simple, perfectly illustrate this point. They introduce us to the properties of zero in multiplication, the commutative property, and the very definition of multiplication itself. This article will unpack these concepts, providing a solid foundation for further mathematical exploration.
Understanding Multiplication: Beyond Repeated Addition
Before diving into specific examples, let's define multiplication. While often introduced as repeated addition (e.g., 2 x 3 is the same as 2 + 2 + 2), multiplication is more fundamentally about scaling. It represents the process of increasing or decreasing a quantity by a certain factor. When we multiply 2 by 3, we're essentially scaling the quantity 2 three times. This scaling perspective becomes particularly important when dealing with non-integer numbers or more abstract mathematical concepts.
The Role of Zero: The Multiplicative Identity
Zero holds a unique position in mathematics. In addition, it acts as the additive identity (adding zero to any number doesn't change its value). In multiplication, zero acts as the multiplicative annihilator. This means that multiplying any number by zero always results in zero. This is why 0 x 2 = 0. No matter how many times you add zero to itself, the result remains zero. This property is fundamental to many mathematical operations and is crucial for solving equations and understanding various mathematical structures.
Let's visualize this with a simple example. Imagine you have zero apples. If you multiply that number of apples by two, you still have zero apples. This intuitively demonstrates the multiplicative annihilation property of zero. This concept extends to any number, not just 2. 0 x 100 = 0, 0 x -5 = 0, and 0 x any number = 0.
Exploring 2 x 1: The Multiplicative Identity and the Commutative Property
The expression "2 x 1" introduces another important mathematical concept: the multiplicative identity. The number 1 is the multiplicative identity because multiplying any number by 1 leaves the number unchanged. Therefore, 2 x 1 = 2. This is because scaling the number 2 by a factor of one means the quantity remains the same.
Furthermore, "2 x 1" illustrates the commutative property of multiplication. The commutative property states that the order of the numbers in a multiplication operation does not affect the result. This means that 2 x 1 is the same as 1 x 2, both equaling 2. This property isn't always true in all mathematical operations (subtraction and division are not commutative), making it a significant characteristic of multiplication. Imagine having two rows of one apple each. The total number of apples is the same as having one row of two apples. This visual representation clearly demonstrates the commutative property.
Practical Applications: Real-World Examples
The principles embedded in "0 x 2" and "2 x 1" are not just abstract mathematical concepts; they have wide-ranging practical applications.
-
Inventory Management: Imagine a warehouse with zero units of a particular product. Multiplying the quantity (0) by any number of orders (e.g., 2) still results in zero units available.
-
Financial Calculations: Calculating interest on a zero-balance account will always result in zero interest, reflecting the multiplicative annihilation property of zero.
-
Measurement and Scaling: Imagine enlarging a photograph by a factor of one. The enlarged photograph will be identical in size to the original, illustrating the multiplicative identity. Enlarging a photograph by a factor of two will double its size.
-
Programming and Computer Science: These basic multiplication operations are fundamental to countless algorithms and computations within computer programs. They are the building blocks of more complex mathematical functions and calculations.
Expanding the Understanding: Beyond the Basics
The simplicity of "0 x 2" and "2 x 1" belies their significance. They provide a foundational understanding of:
-
The properties of zero: Zero's role as the multiplicative annihilator is crucial for various mathematical operations.
-
The concept of multiplication: Moving beyond repeated addition to the idea of scaling helps students grasp multiplication more deeply.
-
The commutative property: Understanding that the order of numbers doesn't change the outcome in multiplication is a significant step toward mathematical fluency.
-
The multiplicative identity: Recognizing the role of 1 in maintaining the original quantity during multiplication is critical.
These concepts lay the groundwork for more complex topics like algebra, calculus, and linear algebra. A solid grasp of these fundamentals is essential for success in higher-level mathematics and related fields.
Addressing Common Questions (FAQ)
-
Q: Why is anything multiplied by zero always zero?
-
A: Multiplication can be visualized as repeated addition. Multiplying by zero means adding a number zero times, resulting in a sum of zero. Alternatively, multiplying by zero means scaling the quantity to zero, effectively reducing it to nothing.
-
Q: Is there a number that, when multiplied by zero, does not result in zero?
-
A: No. The multiplicative annihilation property of zero is a fundamental axiom of arithmetic. There is no exception to this rule.
-
Q: Why is 1 called the multiplicative identity?
-
A: The multiplicative identity is a number that, when multiplied by any other number, leaves that other number unchanged. 1 satisfies this condition. Multiplying any number by 1 simply leaves the number as it is.
-
Q: How does understanding 0 x 2 and 2 x 1 help in advanced mathematics?
-
A: These simple expressions establish the foundational understanding of properties of numbers which become crucial when dealing with more complex concepts like abstract algebra, matrices, and vector spaces. A strong grasp of these basics provides a solid foundation for further learning.
Conclusion: Mastering the Fundamentals
The seemingly simple equations, "0 x 2" and "2 x 1," serve as powerful gateways to a deeper understanding of fundamental mathematical principles. Mastering these concepts is crucial, not just for academic success, but for developing a robust mathematical intuition that extends far beyond the realm of simple arithmetic. Understanding the properties of zero, the concept of multiplication as scaling, the commutative property, and the multiplicative identity provides a bedrock upon which more complex mathematical knowledge can be built. By grasping these fundamentals, learners are empowered to tackle more challenging mathematical concepts with confidence and understanding. The seemingly trivial becomes the extraordinarily significant when viewed through the lens of mathematical foundations. So, embrace the power of the basics – they are the key to unlocking a world of mathematical possibilities.
Latest Posts
Latest Posts
-
Salt Is Alkaline Or Acidic
Sep 23, 2025
-
9 Repeating As A Fraction
Sep 23, 2025
-
Does The Series 1 N Converge
Sep 23, 2025
-
How Many Valence Electrons Oxygen
Sep 23, 2025
-
Define Quantity Demanded In Economics
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 0 X 2 2x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.