1 1 X 1 1
zacarellano
Sep 20, 2025 · 6 min read
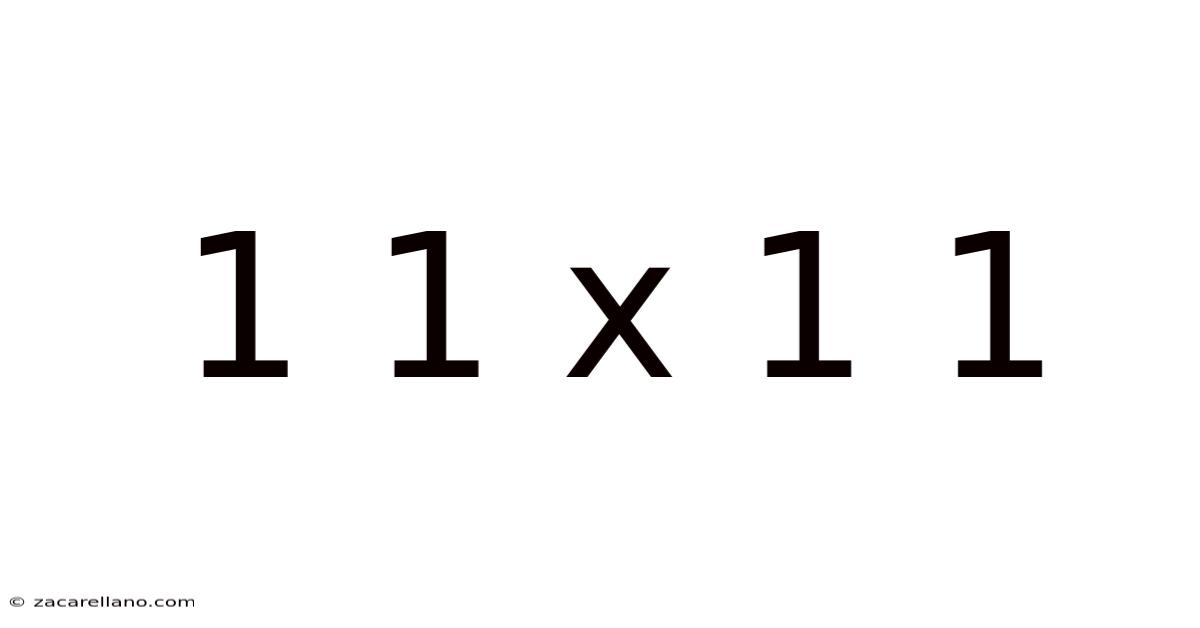
Table of Contents
Decoding 11 x 11: Exploring Multiplication, Squares, and Beyond
Understanding multiplication is a fundamental building block in mathematics. While seemingly simple, the operation holds a depth of significance extending far beyond basic arithmetic. This article delves into the seemingly straightforward calculation of 11 x 11, exploring its implications within various mathematical contexts, unraveling its underlying principles, and showcasing its relevance in more advanced concepts. We'll move beyond the simple answer of 121 to uncover the rich mathematical tapestry woven within this seemingly simple equation.
The Fundamentals: 11 x 11 = 121
At its core, 11 x 11 represents a multiplication problem. It asks: "What is the result of adding eleven groups of eleven?" The straightforward answer, readily obtained through traditional multiplication methods or even mental arithmetic, is 121. This is the foundation upon which we build our understanding.
Beyond the Basic Calculation: Understanding Squares
The equation 11 x 11 is a special case of squaring a number. A square number is the result of multiplying a whole number by itself. In mathematical notation, we represent this as n², where 'n' is the whole number. Therefore, 11 x 11 can be expressed as 11². This concept is crucial in various areas of mathematics, including geometry, algebra, and calculus.
Understanding squares allows us to visualize the problem geometrically. Imagine a square with sides of 11 units each. The area of this square is 11 x 11 = 121 square units. This geometric representation provides a tangible understanding of the abstract concept of squaring.
Methods for Calculating 11 x 11
While the answer is easily obtained using a calculator or simple multiplication, let's explore alternative methods that enhance our understanding of the underlying principles:
-
Traditional Multiplication: This involves the standard long multiplication method taught in elementary school. It's a methodical approach suitable for all multiplication problems.
-
Distributive Property: We can break down 11 as (10 + 1). Applying the distributive property, we get: (10 + 1) x (10 + 1) = (10 x 10) + (10 x 1) + (1 x 10) + (1 x 1) = 100 + 10 + 10 + 1 = 121. This method demonstrates a deeper understanding of how multiplication works.
-
Mental Arithmetic: With practice, you can learn to calculate 11 x 11 mentally. One common technique involves recognizing that 11 squared is the same as (10 + 1) squared. This can be quickly solved using the binomial expansion, which we'll cover later.
-
Patterns in Multiplication: Observe the pattern in multiplying numbers ending in 1:
- 1 x 1 = 1
- 11 x 11 = 121
- 111 x 111 = 12321
- 1111 x 1111 = 1234321
This pattern illustrates a fascinating connection between numbers and their squares. The pattern continues, although the numbers become significantly larger.
Applications of 11 x 11 and Squaring
The concept of squaring, exemplified by 11 x 11, finds numerous applications across diverse fields:
-
Geometry: As previously mentioned, calculating the area of a square. This extends to calculating volumes of cubes and other geometric problems.
-
Algebra: Squaring is a fundamental operation in algebraic manipulation, frequently encountered in solving equations and simplifying expressions. For instance, expanding expressions like (x + 11)² utilizes the concept of squaring.
-
Physics: Many physical formulas involve squaring, especially in relation to calculating areas, volumes, velocities, and energies. Kinetic energy, for example, is calculated using the formula KE = 1/2mv², where v² represents the square of velocity.
-
Computer Science: Squaring is a basic operation in various computational algorithms and data structures.
-
Finance: Compound interest calculations often involve squaring and higher powers of numbers.
Exploring Related Mathematical Concepts
Let's delve into related mathematical concepts connected to 11 x 11:
-
Binomial Expansion: The expression (a + b)² expands to a² + 2ab + b². Applying this to (10 + 1)², we get 10² + 2(10)(1) + 1² = 100 + 20 + 1 = 121. This demonstrates a powerful algebraic tool for expanding squared binomials.
-
Pascal's Triangle: Pascal's triangle is a geometrical arrangement of numbers where each number is the sum of the two numbers directly above it. The coefficients in the binomial expansion (a + b)ⁿ can be found in Pascal's triangle. For (10 + 1)², the coefficients are 1, 2, 1, which correspond to the expansion 1(10)² + 2(10)(1) + 1(1)².
-
Number Theory: Exploring the properties of 121 within number theory reveals it's a composite number (not prime) with factors 1, 11, and 121. It's also a perfect square and an odd number.
Advanced Concepts and Extensions
Moving beyond the basics, let's consider further extensions:
-
Higher Powers of 11: Consider calculating 11³, 11⁴, and so on. These calculations demonstrate the exponential growth of numbers.
-
Matrices and Linear Algebra: In linear algebra, multiplying matrices involves similar concepts to scalar multiplication, providing a more complex application of these fundamental ideas.
-
Calculus: Derivatives and integrals involve concepts related to rates of change and areas under curves, respectively. These concepts are built upon a foundation of basic arithmetic, including multiplication and squaring.
Frequently Asked Questions (FAQ)
-
Q: What is the easiest way to calculate 11 x 11?
- A: The easiest way depends on your comfort level. For many, simply memorizing that 11 x 11 = 121 is sufficient. Alternatively, the distributive property or mental math techniques can be used.
-
Q: Is 121 a prime number?
- A: No, 121 is not a prime number. It is divisible by 1, 11, and 121, making it a composite number.
-
Q: What are some real-world applications of squaring numbers?
- A: Squaring numbers has numerous real-world applications in areas such as geometry (calculating areas and volumes), physics (calculating energy and velocity), and finance (calculating compound interest).
-
Q: How does understanding 11 x 11 help me with more advanced math?
- A: Understanding 11 x 11, and more broadly, the concept of squaring, provides a foundation for understanding more advanced mathematical concepts such as binomial expansion, Pascal's triangle, and algebraic manipulation.
Conclusion: A Deeper Appreciation of a Simple Calculation
The seemingly simple calculation of 11 x 11 = 121 opens a door to a vast landscape of mathematical concepts and applications. From its geometric representation as the area of a square to its role in advanced algebraic manipulations and real-world problem-solving, this fundamental operation highlights the interconnectedness of mathematical ideas. By exploring different methods of calculation and understanding its applications, we gain a deeper appreciation for the richness and beauty inherent within even the most basic mathematical operations. The seemingly simple equation serves as a gateway to a more profound understanding of the mathematical world. Continue exploring, experimenting, and discovering the wonders of mathematics—the journey is far more rewarding than the destination.
Latest Posts
Latest Posts
-
Midpoint Riemann Sum With Table
Sep 20, 2025
-
Ap Calc Bc Series Review
Sep 20, 2025
-
What Is Rural Urban Migration
Sep 20, 2025
-
Effect Of Temp On Equilibrium
Sep 20, 2025
-
3rd Grade Division Word Problems
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 1 1 X 1 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.