1 2 N 1 N
zacarellano
Sep 18, 2025 · 6 min read
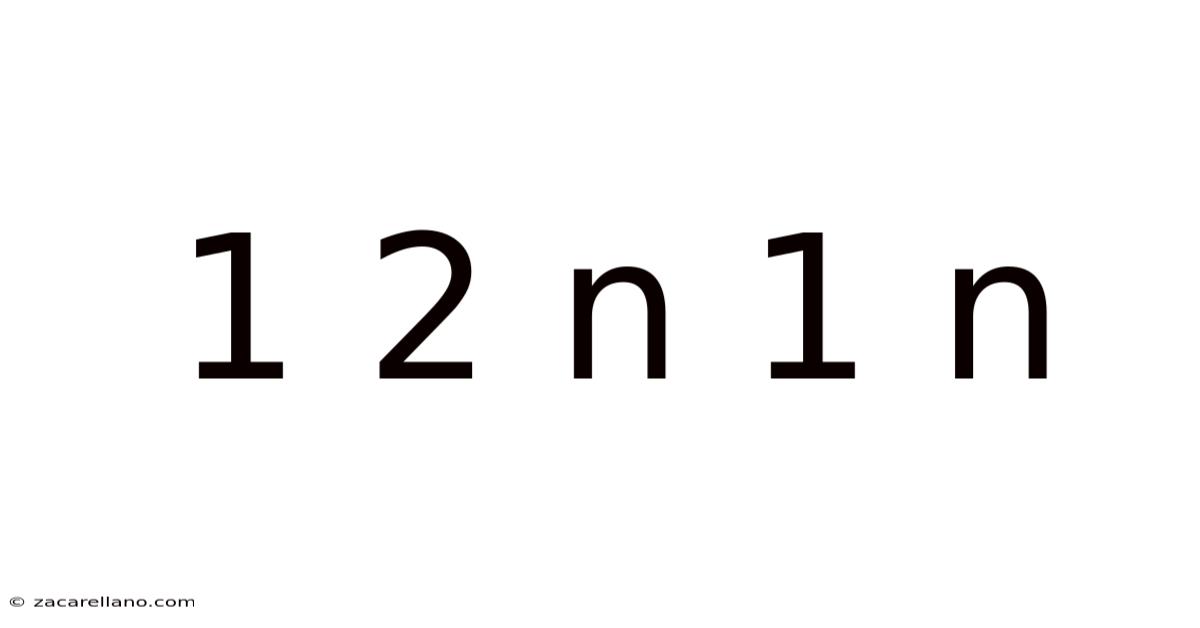
Table of Contents
Decoding the Enigma: A Deep Dive into the 1, 2, n, 1, n Sequence
The sequence "1, 2, n, 1, n" might seem deceptively simple at first glance. However, this seemingly innocuous series of numbers holds a fascinating depth, capable of sparking explorations across various mathematical fields and real-world applications. This article delves into the intricacies of this sequence, exploring its potential meanings, interpretations, and hidden mathematical properties. We'll unravel its mysteries, examining its applications in different contexts and answering frequently asked questions. Understanding this seemingly simple sequence can unlock a deeper appreciation for the beauty and complexity of mathematics.
Introduction: Unpacking the Sequence's Potential Meanings
The sequence "1, 2, n, 1, n" lacks a universally defined mathematical meaning. Its interpretation depends heavily on the context in which it's presented. This ambiguity, however, is precisely what makes it intriguing. It could represent a pattern within a larger sequence, a snippet of a recursive function, or even a symbolic representation within a specific problem domain. This article will explore several potential interpretations, focusing on how the variable 'n' adds a layer of complexity and possibility. We'll consider scenarios where 'n' represents a specific number, a variable in an equation, or even a placeholder for a broader concept.
Interpretations and Applications: Exploring the Possibilities
1. As a Building Block for Larger Sequences:
The sequence could serve as a fundamental repeating unit within a more extensive sequence. Imagine a scenario where 'n' cycles through a set of values, creating a longer, more intricate pattern. For instance, if n = 3, the sequence could extend to: 1, 2, 3, 1, 3, 1, 2, 4, 1, 4, 1, 2, 5, 1, 5... and so on. The possibilities here are endless, depending on the rule governing the progression of 'n'. This interpretation highlights the sequence's potential as a generative element in mathematical modeling.
2. Representation within Recursive Functions:
The sequence could be a part of a recursively defined function. Recursive functions are functions that call themselves within their own definition. The sequence "1, 2, n, 1, n" might represent intermediate steps or results within a larger recursive process. The value of 'n' could be dynamically determined within the recursive call, leading to a complex and potentially unpredictable output. This application emphasizes the sequence’s role in algorithmic thinking and computational processes.
3. Symbolic Representation in Problem Solving:
In certain problem-solving contexts, the sequence might function as a symbolic representation. For example, consider a scenario involving a system with two distinct states (represented by 1 and 2) and a variable number of intermediate states ('n'). The sequence could then represent the transitions between these states within the system. The '1' and 'n' could signify specific events or processes within the larger system, and the '2' could denote a transitional phase. This approach demonstrates the sequence's potential as a tool for abstract representation and conceptual modeling.
4. Encoding and Cryptography:
While highly speculative without additional context, the sequence could potentially be part of a simple encoding or cryptography scheme. The value of 'n' could serve as a key, altering the encoded message. Such a system, however, would be extremely rudimentary and easily broken with a bit of cryptanalysis. This showcases the importance of context and complexity in secure coding practices.
Mathematical Exploration of the Sequence: Discovering Hidden Patterns
Analyzing the sequence mathematically requires careful consideration of the role of the variable 'n'. We can explore several mathematical avenues:
-
Arithmetic Progression: If 'n' is assumed to be an element of an arithmetic progression, the overall sequence becomes far more complex. This would necessitate an additional rule defining how 'n' changes. For example, if 'n' increases by one each time, we’d have: 1, 2, 3, 1, 3, 1, 2, 4, 1, 4, 1, 2, 5… This opens possibilities for exploring patterns related to arithmetic sequences and series.
-
Geometric Progression: Similarly, if ‘n’ is a part of a geometric progression, the implications change entirely. The resulting sequence would then exhibit a different type of growth, potentially leading to exponential patterns or chaotic behavior depending on the common ratio of the geometric progression.
-
Fibonacci-like Sequences: While not a direct Fibonacci sequence, the presence of repeating elements and the variable 'n' opens up avenues to exploring its relationship with Fibonacci-like sequences. Are there any predictable patterns that emerge based on different values of 'n' and their relationship to Fibonacci numbers?
The Significance of the Variable 'n'
The inclusion of 'n' is pivotal. It introduces an element of dynamism and uncertainty, allowing for various interpretations. It shifts the sequence from a static, predetermined list of numbers to a dynamic entity. The behavior of the sequence becomes dependent on the definition and evolution of 'n', giving it far greater analytical potential.
Expanding the Scope: Applications in Other Disciplines
Beyond purely mathematical explorations, the sequence could find applications in other fields. Consider the following:
-
Computer Science: The sequence could represent states in a finite state machine, a fundamental concept in computer science. The value of 'n' could represent a particular state, and the transitions between states could be modeled using the sequence.
-
Music Theory: Abstractly, the sequence might potentially be mapped onto musical notes or rhythms. The value of 'n' could represent variations in tempo or melody.
-
Linguistics: It could be used as a rudimentary code to represent words or phrases, though its simplicity would render it easily decipherable.
Frequently Asked Questions (FAQ)
Q: What is the mathematical definition of the 1, 2, n, 1, n sequence?
A: There isn't a single, universally accepted mathematical definition. Its meaning depends entirely on the context in which it's used.
Q: Does this sequence have any known applications in advanced mathematics?
A: Currently, there aren't established applications in advanced mathematical fields. However, its structure provides a framework for exploring relationships with other sequences, functions, and mathematical concepts. Further research could reveal unexpected connections.
Q: Can the sequence be generalized to a more complex form?
A: Absolutely. The sequence can be generalized by expanding the number of elements, introducing more variables, or defining rules for how 'n' changes. This would create richer and more complex sequences.
Q: What are the limitations of this sequence?
A: Its simplicity is both its strength and weakness. The lack of a fixed definition limits its immediate applicability in specific mathematical contexts. However, this ambiguity opens up broader interpretative possibilities.
Conclusion: A Journey of Exploration and Discovery
The sequence "1, 2, n, 1, n," while seemingly simple, offers a compelling starting point for mathematical exploration. Its open-ended nature encourages creative thinking, providing a canvas for developing complex sequences, functions, and models. The variable 'n' is the key, injecting dynamism and allowing for various interpretations across different fields. Whether it's seen as a building block for larger sequences, a representation within recursive functions, or a symbolic tool in problem-solving, the sequence's inherent ambiguity is its most captivating feature. Its exploration invites further investigation and reveals the endless possibilities inherent in even the simplest mathematical patterns. The true value lies not in a single, definitive answer but in the process of uncovering its potential meanings and applications. This exploration underscores the richness and boundless nature of mathematical inquiry.
Latest Posts
Latest Posts
-
Thirteen Colonies Map New England
Sep 18, 2025
-
Ap Computer Science Principles Textbook
Sep 18, 2025
-
Algebra Equations That Equal 2
Sep 18, 2025
-
Example Of An Area Model
Sep 18, 2025
-
Difference Between Variation And Adaptation
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 1 2 N 1 N . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.