1 2 Subtract 1 4
zacarellano
Sep 18, 2025 · 7 min read
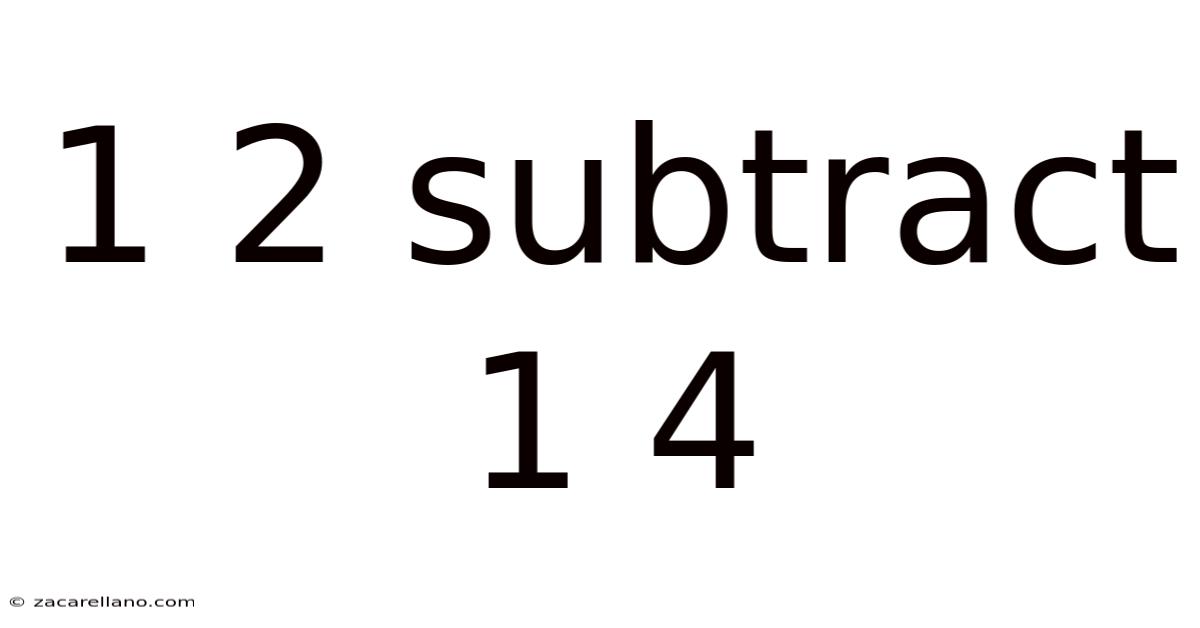
Table of Contents
Decoding 1 2 Subtract 1 4: A Deep Dive into Subtraction with Mixed Numbers
This article explores the seemingly simple yet often confusing mathematical operation: subtracting mixed numbers, specifically focusing on the problem "1 2 subtract 1 4". We'll break down this calculation step-by-step, providing a thorough understanding of the underlying principles and offering strategies to solve similar problems with confidence. This explanation will cover various methods, addressing potential misconceptions and building a solid foundation in arithmetic. Understanding mixed number subtraction is crucial for building a strong base in mathematics, essential for progressing to more advanced concepts.
Understanding Mixed Numbers
Before diving into the subtraction problem, let's clarify what mixed numbers are. A mixed number is a combination of a whole number and a proper fraction. For instance, "1 2" represents one whole unit and two-thirds of another. It's a way of expressing a number that lies between two whole numbers. Understanding this representation is key to performing operations involving mixed numbers.
The Challenge: 1 2 Subtract 1 4
The problem "1 2 subtract 1 4" presents a common challenge in arithmetic: subtracting mixed numbers where the fractional part of the subtrahend (the number being subtracted) is larger than the fractional part of the minuend (the number being subtracted from). This requires a specific approach that involves borrowing from the whole number portion.
Method 1: Converting to Improper Fractions
One effective method to solve this type of subtraction problem is by converting both mixed numbers into improper fractions. An improper fraction has a numerator larger than or equal to its denominator.
-
Step 1: Convert 1 2 to an improper fraction. To do this, multiply the whole number (1) by the denominator (3) and add the numerator (2). This gives us 1 * 3 + 2 = 5. The denominator remains the same, so 1 2 becomes 5/3.
-
Step 2: Convert 1 4 to an improper fraction. Following the same process, we multiply the whole number (1) by the denominator (4) and add the numerator (1). This gives us 1 * 4 + 1 = 5. The denominator remains the same, so 1 4 becomes 5/4.
-
Step 3: Perform the subtraction. Now we have the problem 5/3 - 5/4. To subtract fractions, they must have a common denominator. The least common multiple (LCM) of 3 and 4 is 12. We convert both fractions to have a denominator of 12:
- 5/3 = (5 * 4) / (3 * 4) = 20/12
- 5/4 = (5 * 3) / (4 * 3) = 15/12
-
Step 4: Subtract the numerators. Now we subtract the numerators while keeping the denominator the same: 20/12 - 15/12 = 5/12.
Therefore, 1 2 subtract 1 4 equals 5/12.
Method 2: Borrowing and Subtracting
Another approach involves borrowing from the whole number portion. This method is often preferred for its intuitive visual representation.
-
Step 1: Recognize the need to borrow. We cannot directly subtract 1/4 from 2/3 because 1/4 is larger. We need to borrow one unit from the whole number 1 in the minuend (1 2/3).
-
Step 2: Borrow from the whole number. Borrowing one from the whole number 1, and adding it to the fractional part, gives us: 1 is equivalent to 3/3. Adding this to the existing 2/3, we get 3/3 + 2/3 = 5/3. Now our minuend becomes 0 5/3.
-
Step 3: Rewrite the subtraction. Our problem is now rewritten as 0 5/3 - 1 1/4. This highlights the challenge more clearly: we need a common denominator to continue.
-
Step 4: Find a common denominator. The LCM of 3 and 4 is 12.
-
Step 5: Convert to equivalent fractions. Converting 5/3 and 1/4 to twelfths, we have:
- 5/3 = (54)/(34) = 20/12
- 1/4 = (13)/(43) = 3/12
-
Step 6: Perform the subtraction. We now have 20/12 - 3/12 = 17/12
-
Step 7: Simplify 17/12 is an improper fraction, convert it to mixed fraction to get 1 5/12
This method, while seemingly more complex initially, builds a strong understanding of the underlying principle of borrowing in subtraction.
Method 3: Decomposition Method
This method involves breaking down the mixed numbers into their whole and fractional components for easier subtraction.
-
Step 1: Separate whole and fractional parts: We have 1 2/3 - 1 1/4. Let's separate the whole numbers and the fractions: (1 - 1) + (2/3 - 1/4)
-
Step 2: Subtract the whole numbers: 1 - 1 = 0.
-
Step 3: Find a common denominator for the fractions: The LCM of 3 and 4 is 12.
-
Step 4: Convert fractions to equivalent fractions:
- 2/3 = 8/12
- 1/4 = 3/12
-
Step 5: Subtract the fractions: 8/12 - 3/12 = 5/12
-
Step 6: Combine the results: 0 + 5/12 = 5/12
This approach clearly separates the process, making it easy to follow and understand.
Addressing Common Mistakes
Many students struggle with subtracting mixed numbers, often making mistakes in converting fractions or understanding the borrowing process. Here are some common errors and how to avoid them:
-
Incorrect conversion to improper fractions: Double-check your multiplication and addition when converting mixed numbers to improper fractions. A single error can throw off the entire calculation.
-
Forgetting to find a common denominator: Remember that you must have a common denominator before subtracting fractions. Failing to do so leads to incorrect results.
-
Incorrect borrowing: When borrowing from the whole number, ensure you add the equivalent fraction correctly. Understand that borrowing 1 from the whole number is equivalent to adding the denominator to the existing numerator.
-
Ignoring simplification: Always simplify your final answer to its lowest terms. This ensures your answer is presented in its most efficient form.
Further Exploration and Practice
Mastering mixed number subtraction requires practice. Try solving similar problems, varying the numbers and the complexity of the fractions involved. Experiment with all three methods explained above to find the one that best suits your learning style and understanding. You can create your own practice problems or use online resources and textbooks.
Frequently Asked Questions (FAQ)
Q: Can I always use the improper fraction method?
A: Yes, the improper fraction method works for all subtraction problems involving mixed numbers. It's a reliable and consistent approach.
Q: Which method is the easiest?
A: The "easiest" method depends on your individual preference and understanding. Some students find the improper fraction method straightforward, while others prefer the visual approach of borrowing. Experiment to find what works best for you.
Q: What if the whole number in the subtrahend is larger?
A: If the whole number of the subtrahend is larger than the minuend, the result will be a negative number. For example, 1 2/3 - 2 1/4 would result in a negative mixed number.
Q: What happens if the fractions are equal?
A: If the fractional parts of both mixed numbers are equal, the subtraction focuses solely on the whole number difference. For example, 2 3/5 - 1 3/5 = 1.
Q: Can I use a calculator?
A: While a calculator can provide the answer, it is crucial to understand the underlying mathematical principles. Using a calculator without comprehending the method defeats the purpose of learning the concept. Use calculators only for checking your work after attempting the solution manually.
Conclusion
Subtracting mixed numbers like "1 2 subtract 1 4" might seem daunting at first, but with a clear understanding of the principles of improper fractions, borrowing, and the decomposition method, you can confidently tackle such problems. Remember to practice regularly, identify your common mistakes, and choose the method that best suits your learning style. Mastering this skill forms a crucial foundation for more advanced mathematical concepts, building your confidence and proficiency in arithmetic. By consistently applying these techniques, you'll develop a robust understanding of mixed number subtraction and improve your overall mathematical skills.
Latest Posts
Latest Posts
-
Standard Form And Unit Form
Sep 18, 2025
-
Is Water Denser Than Air
Sep 18, 2025
-
Reflected On The Y Axis
Sep 18, 2025
-
The Circumference Of The World
Sep 18, 2025
-
The Surrender Of Breda Painting
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 1 2 Subtract 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.