1 4 Minus 1 3
zacarellano
Sep 17, 2025 · 5 min read
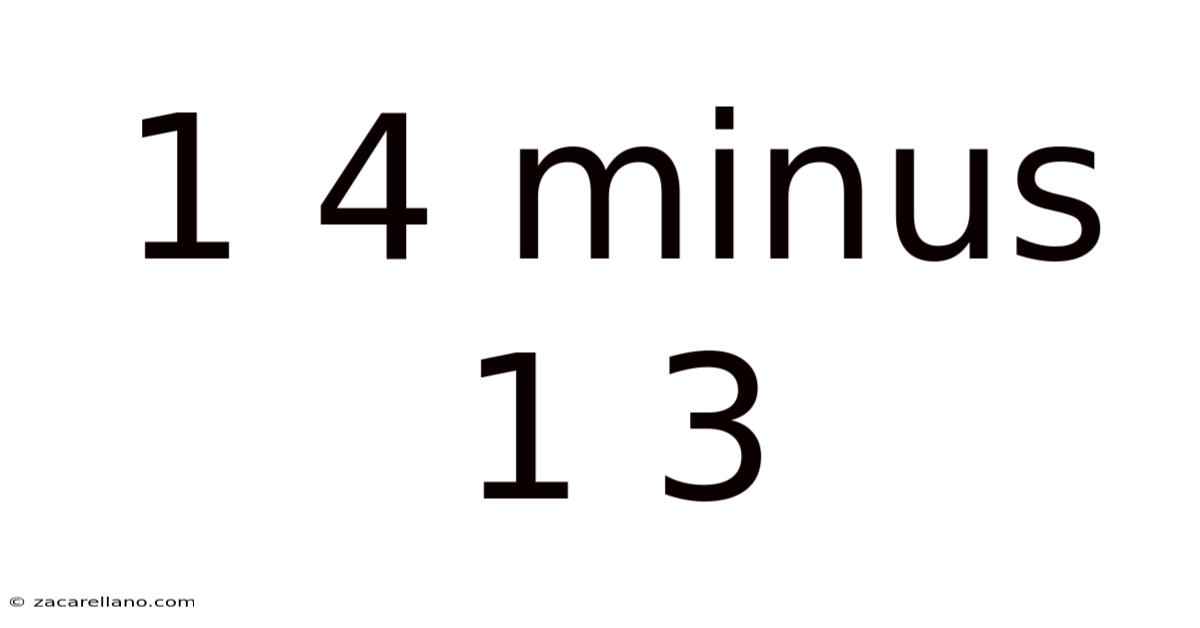
Table of Contents
Decoding 14 Minus 13: A Deep Dive into Subtraction and Number Systems
This article explores the seemingly simple subtraction problem, "14 minus 13," delving far beyond the immediate answer. We'll examine the fundamental principles of subtraction, its representation in various number systems, practical applications, and even touch upon the philosophical implications of this basic arithmetic operation. Understanding this seemingly simple equation unlocks a deeper appreciation for mathematics and its foundational concepts.
Introduction: More Than Just a Simple Subtraction
At first glance, "14 minus 13" appears trivial – the answer is obviously 1. However, this seemingly simple problem provides a gateway to explore several crucial mathematical concepts. This exploration will cover the basics of subtraction, its role in different number systems (like binary and Roman numerals), and its relevance in real-world scenarios, all while maintaining a clear and accessible style. We’ll also address frequently asked questions and offer concluding thoughts that emphasize the significance of grasping fundamental mathematical principles.
Understanding Subtraction: The Basics
Subtraction is one of the four basic arithmetic operations, alongside addition, multiplication, and division. It represents the process of removing a quantity from another. In the equation "14 - 13 = 1," we start with a quantity of 14 and remove 13, leaving us with a remainder of 1. This can be visualized in numerous ways:
- Using objects: Imagine having 14 apples. If you give away 13, you are left with 1 apple.
- Number line: On a number line, starting at 14 and moving 13 units to the left brings you to 1.
- Set theory: Subtraction can be understood as removing elements from a set. A set of 14 elements, after removing 13 elements, leaves a set with 1 element.
Exploring Different Number Systems
While our usual decimal (base-10) system is familiar, representing "14 minus 13" in other systems reveals the universality of subtraction and the elegance of mathematical principles.
-
Binary (Base-2): In binary, 14 is represented as 1110 and 13 as 1101. Subtracting these binary numbers involves borrowing (similar to carrying in addition), a process which can be more complex than in base-10, but still yields the same result: 0001 (which is 1 in decimal).
-
Roman Numerals: 14 is XIV and 13 is XIII. Subtracting XIII from XIV is equivalent to removing three I's and one X from XIV. This leaves one I, hence, I (1 in decimal).
This demonstrates that the concept of subtraction remains consistent regardless of the number system used. The methods might vary, but the underlying principle remains the same.
Subtraction in Real-World Applications
The seemingly simple act of subtracting 13 from 14 finds its application in a multitude of real-world scenarios:
-
Financial transactions: Calculating change after a purchase, tracking expenses, and determining profit margins all involve subtraction. If an item costs $13 and you pay with $14, your change is $1.
-
Measurement: Determining the difference between two lengths, weights, or volumes utilizes subtraction. If one object is 14 cm long and another is 13 cm long, the difference is 1 cm.
-
Inventory management: Tracking stock levels in a warehouse or shop requires subtracting the number of items sold from the initial inventory.
-
Data analysis: Subtracting values is crucial in comparing data sets, calculating differences, and identifying trends. For example, comparing sales figures from two consecutive months involves subtraction.
The Mathematical Properties of Subtraction
Understanding the mathematical properties of subtraction provides a more comprehensive grasp of its role in arithmetic.
-
Not commutative: Subtraction is not commutative, meaning that the order of the numbers matters. 14 - 13 ≠ 13 - 14. The result differs depending on which number is subtracted from the other.
-
Not associative: Subtraction is not associative, meaning that the grouping of numbers affects the result. (14 - 13) - 2 ≠ 14 - (13 - 2). The order of operations is crucial.
-
Identity element: Zero is the identity element for subtraction; subtracting zero from a number doesn't change its value (e.g., 14 - 0 = 14).
-
Inverse operation of addition: Subtraction is the inverse operation of addition. If you add 13 to 1, you get 14.
Beyond the Basics: Negative Numbers and Subtraction
Our initial problem, 14 - 13, results in a positive number. However, subtraction can also lead to negative numbers. For instance, 13 - 14 = -1. Understanding negative numbers is critical for extending our understanding of subtraction and its applications in more complex mathematical contexts. The number line extends infinitely in both the positive and negative directions, accommodating all possible results of subtraction.
Frequently Asked Questions (FAQ)
-
Q: What is the simplest way to explain 14 minus 13 to a child?
- A: Imagine you have 14 candies, and you eat 13. How many candies do you have left? Just one!
-
Q: Why is subtraction important?
- A: Subtraction is essential for solving countless real-world problems, from balancing a budget to measuring distances. It’s a foundational skill for more advanced mathematics.
-
Q: Are there different methods for subtraction?
- A: Yes, there are various methods, including the standard algorithm, decomposition, and using a number line. The best method often depends on the numbers involved and individual preference.
-
Q: Can I use a calculator for 14 minus 13?
- A: While a calculator can certainly perform the calculation, understanding the underlying principles of subtraction is far more valuable than simply obtaining the answer.
Conclusion: The Enduring Significance of Simple Subtraction
The seemingly simple problem, "14 minus 13," opens a door to a rich world of mathematical concepts. From the fundamental principles of subtraction to its representation in different number systems and its countless real-world applications, this equation encapsulates the power and elegance of mathematics. Mastering this foundational operation is not just about getting the right answer (which is 1); it's about building a solid understanding that will support further exploration of more complex mathematical concepts. The ability to grasp and apply basic arithmetic operations like subtraction lays the groundwork for success in various fields, highlighting the enduring significance of this seemingly simple yet fundamental mathematical operation. Continuing to explore and understand these basic building blocks empowers us to tackle increasingly sophisticated mathematical challenges with confidence and competence.
Latest Posts
Latest Posts
-
How To Solve Lagrange Multipliers
Sep 17, 2025
-
What Is Nadph In Photosynthesis
Sep 17, 2025
-
What Is Ak Selected Species
Sep 17, 2025
-
Ap Gov Unit One Review
Sep 17, 2025
-
Little Red Riding Hood Quote
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1 4 Minus 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.