1 4 X 5 6
zacarellano
Sep 20, 2025 · 5 min read
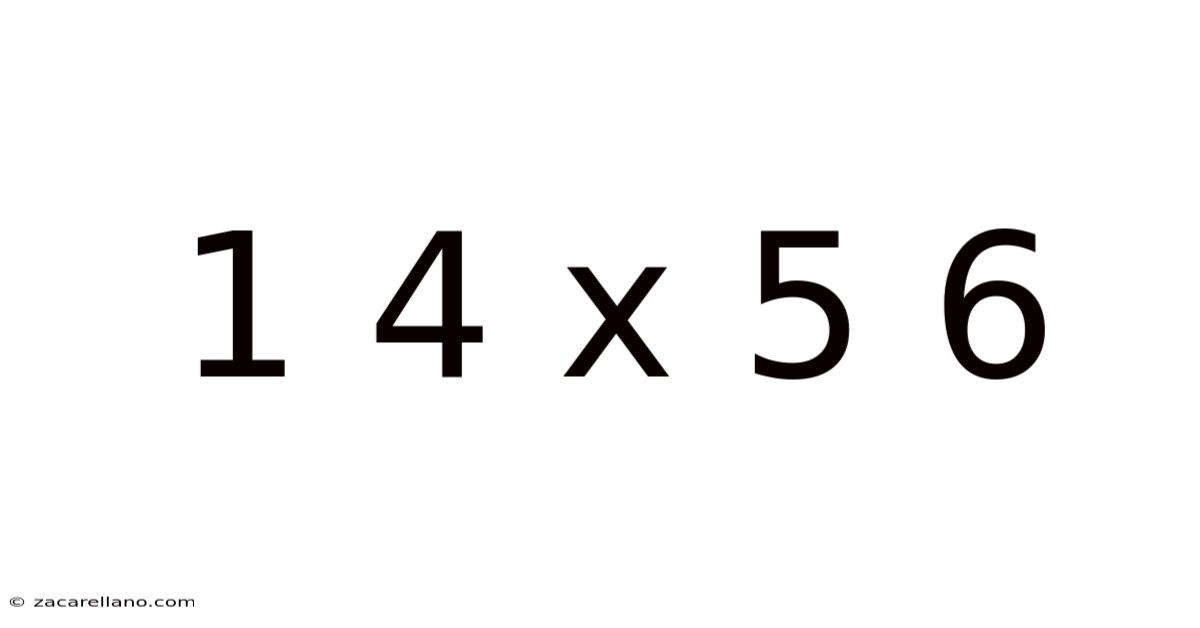
Table of Contents
Decoding 1 4 x 5 6: Exploring the World of Ratio, Proportion, and Scale
This article delves into the seemingly simple expression "1 4 x 5 6," exploring its multifaceted implications within mathematics, particularly concerning ratios, proportions, and scale. We'll unpack its meaning, demonstrate its applications in real-world scenarios, and address frequently asked questions. Understanding this fundamental concept lays the groundwork for more advanced mathematical principles and problem-solving across various fields.
Introduction: Unveiling the Mystery of Ratios
At first glance, "1 4 x 5 6" might seem like an arbitrary sequence of numbers. However, its true power lies in its representation of a ratio, a fundamental mathematical concept describing the quantitative relationship between two or more values. In this case, we have two distinct ratios: 1:4 and 5:6. These ratios represent comparisons, showing how one quantity relates to another. Understanding ratios is crucial for numerous applications, from scaling recipes to designing buildings, to understanding financial markets.
Understanding Ratios and Proportions
A ratio compares two quantities using division. The ratio 1:4 can be interpreted as "1 part to 4 parts" or "1 for every 4." Similarly, 5:6 signifies "5 parts to 6 parts" or "5 for every 6". When two ratios are equal, we have a proportion. Proportions are incredibly useful because they allow us to solve for unknown values when we know the relationship between different quantities. For example, if we know that the ratio of boys to girls in a class is 1:4, and there's 1 boy, we can use this proportion to determine the number of girls (4).
Mathematical Representation and Manipulation
Ratios can be expressed in several ways:
- Colon notation: 1:4, 5:6
- Fraction notation: 1/4, 5/6
- Decimal notation: 0.25, 0.833...
The choice of representation often depends on the context and the specific calculation being performed. Converting between these forms is straightforward. For instance, the ratio 1:4 is equivalent to the fraction 1/4, which simplifies to the decimal 0.25.
Exploring the "x" in 1 4 x 5 6
The "x" symbol in "1 4 x 5 6" typically indicates a multiplicative relationship or a comparison between the two ratios. It suggests a scenario where we might need to determine if the two ratios are equivalent, find a missing value in a proportion involving these ratios, or scale one ratio to match the other. Let's explore these scenarios:
Scenario 1: Determining Equivalence
Are the ratios 1:4 and 5:6 equivalent? To determine this, we can cross-multiply:
1 x 6 = 6 4 x 5 = 20
Since 6 ≠ 20, the ratios 1:4 and 5:6 are not equivalent. This means they represent different proportions.
Scenario 2: Solving Proportions
Let's consider a problem: A recipe calls for 1 cup of sugar for every 4 cups of flour (ratio 1:4). If we want to make a larger batch using 5 cups of sugar, how many cups of flour do we need?
We can set up a proportion:
1/4 = 5/x
Cross-multiplying:
1 * x = 4 * 5 x = 20
Therefore, we need 20 cups of flour.
Scenario 3: Scaling Ratios
Suppose we have a scale model of a building. The scale is 1:4, meaning 1 cm on the model represents 4 cm in reality. We measure a wall on the model to be 5 cm. How long is the actual wall?
Again, we set up a proportion:
1/4 = 5/x
Cross-multiplying:
x = 20 cm
The actual wall is 20 cm long.
Real-World Applications: From Recipes to Engineering
The principles of ratio and proportion permeate various aspects of daily life and professional fields. Some examples include:
- Cooking: Scaling recipes up or down based on the number of servings.
- Mapmaking: Interpreting distances on maps using scales.
- Engineering: Designing structures that maintain proportional relationships between different components.
- Finance: Calculating interest rates and financial ratios.
- Science: Analyzing experimental data and expressing concentrations.
Explaining the Scientific Basis of Ratios and Proportions
The mathematical concepts behind ratios and proportions are grounded in the fundamental principles of measurement and comparison. They allow us to establish relationships between quantities, irrespective of their units. This is because a ratio is a dimensionless quantity; it's a comparison of two quantities of the same kind, eliminating the units in the process. This inherent dimensionless nature makes ratios powerful tools for analysis and prediction across diverse disciplines. Furthermore, proportions provide a framework for solving problems involving unknown variables based on known relationships between quantities.
Frequently Asked Questions (FAQ)
-
Q: What if the ratios involve decimals or fractions? A: The same principles apply. Convert the decimals or fractions to equivalent forms (e.g., fractions to decimals) to simplify calculations.
-
Q: How do I solve proportions with more than two ratios? A: You can still use cross-multiplication techniques, but it might require a more methodical approach involving multiple steps.
-
Q: Can ratios involve more than two numbers? A: Absolutely. For instance, a ratio might compare the amounts of red, blue, and green paint in a mixture (e.g., 2:3:1).
-
Q: What happens if one of the values in the ratio is zero? A: A ratio cannot have a denominator of zero; it's undefined.
-
Q: Are ratios and fractions the same thing? A: While closely related, they have subtle differences. A fraction represents a part of a whole, while a ratio compares two or more quantities. However, ratios can often be expressed as fractions.
Conclusion: Mastering the Power of Proportion
Understanding "1 4 x 5 6" is more than just understanding a simple mathematical expression; it's about grasping the fundamental concept of ratios and proportions. These concepts are crucial tools for problem-solving in countless situations, from everyday tasks to sophisticated scientific and engineering applications. By mastering these principles, you equip yourself with the ability to analyze relationships, solve problems, and make informed decisions across various disciplines. The seemingly simple expression opens doors to a world of mathematical understanding and practical application. Through consistent practice and exploration, you'll unlock the power of proportion and its transformative potential in solving diverse problems and understanding complex relationships. Remember, the journey to mastering ratios and proportions is a gradual process – practice consistently, and you will see your understanding grow exponentially.
Latest Posts
Latest Posts
-
Domain Of X 2 X
Sep 20, 2025
-
Is Denominator Top Or Bottom
Sep 20, 2025
-
Grammar Subject Verb Agreement Exercises
Sep 20, 2025
-
Fractional Vs Simple Distillation Graph
Sep 20, 2025
-
Individuals In A Data Set
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 1 4 X 5 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.