1 8 X 1 8
zacarellano
Sep 17, 2025 · 6 min read
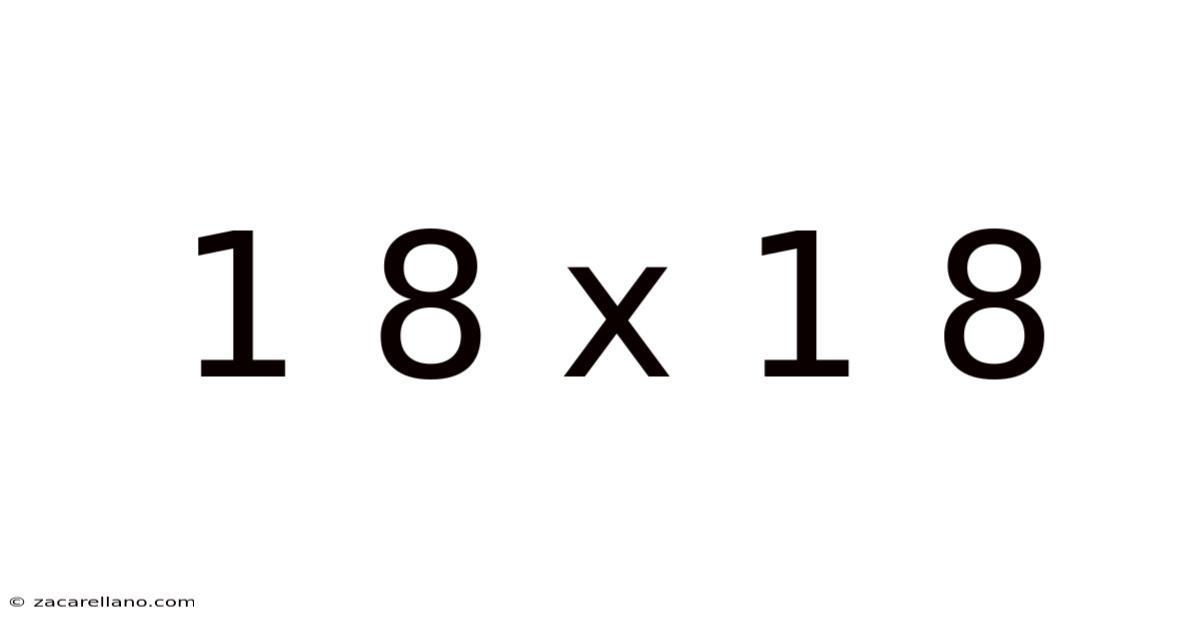
Table of Contents
Decoding 18 x 18: A Deep Dive into its Mathematical and Practical Applications
This article explores the seemingly simple mathematical expression "18 x 18," delving beyond the basic calculation to uncover its multifaceted applications across various fields. We'll explore its significance in algebra, geometry, number theory, and even practical real-world scenarios. Understanding 18 x 18 isn't just about getting the answer; it's about appreciating the underlying mathematical principles and their widespread implications. This will include examining the properties of the number 324 (the product of 18 x 18), its factors, and its role in different mathematical contexts.
Understanding the Basics: 18 x 18 = 324
At its core, 18 x 18 represents a multiplication problem. The simple calculation yields the answer 324. However, this seemingly straightforward equation opens doors to a much richer understanding of mathematics and its applications. Let's explore this in greater detail.
Exploring the Properties of 324
The number 324, the product of 18 multiplied by itself, possesses several interesting mathematical properties:
-
Factors: 324 has numerous factors, reflecting its composite nature. Its factors include 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 81, 108, 162, and 324. This abundance of factors makes it useful in various mathematical problems involving divisibility and factorization.
-
Squares and Square Roots: As the square of 18, 324 is a perfect square. This means it has a whole number as its square root (18). Understanding perfect squares is fundamental in algebra, geometry, and number theory.
-
Divisibility Rules: 324 is divisible by several numbers, including 2, 3, 4, 6, 9, and 12. Knowing divisibility rules helps in simplifying calculations and identifying patterns in numbers.
-
Prime Factorization: The prime factorization of 324 is 2² x 3⁴. This decomposition into prime numbers is crucial in various number theory applications, including finding the greatest common divisor (GCD) and least common multiple (LCM) of numbers.
Applications in Algebra
The equation 18 x 18 = 324 finds applications in various algebraic concepts:
-
Solving Equations: The number 324 can appear in various algebraic equations, requiring solving for an unknown variable. For example, x² = 324 would have a solution of x = ±18.
-
Quadratic Equations: Quadratic equations, involving x², often involve numbers like 324 in their solutions. Understanding the properties of 324 can simplify the process of solving these equations.
-
Polynomial Expansions: 324 might emerge as a coefficient or term in the expansion of polynomials, highlighting the interconnectedness of different algebraic concepts.
-
Sequences and Series: The number 324 could be a term in arithmetic or geometric sequences and series, demonstrating its relevance in sequential patterns.
Applications in Geometry
The number 324 and its relationship to 18 have significant geometric implications:
-
Squares and Rectangles: An 18 x 18 square has an area of 324 square units. This concept is fundamental in calculating areas and perimeters of geometric shapes.
-
Volume Calculations: If we consider a cube with sides of length 18 units, its volume would be 18 x 18 x 18 = 5832 cubic units. This demonstrates the extension of the concept to three-dimensional shapes.
-
Triangles: 324 could represent the area of specific triangles, depending on their base and height. Understanding area calculations is essential in geometry.
-
Circles: While not directly related to the square of 18, understanding area calculations allows us to connect the concept to circle area calculations (πr²) by considering a circle with a related radius or circumference.
Applications in Number Theory
Number theory extensively utilizes the properties of numbers like 324:
-
Divisibility and Factorization: As mentioned earlier, the factors of 324 are central to understanding divisibility rules and factorization techniques.
-
Perfect Squares: The fact that 324 is a perfect square is significant in various number theory theorems and proofs.
-
Modular Arithmetic: The number 324 can be used in modular arithmetic calculations, analyzing remainders after division.
-
Diophantine Equations: 324 might appear in Diophantine equations, which involve finding integer solutions to algebraic equations.
Real-World Applications
Beyond the theoretical realms of mathematics, 18 x 18 = 324 has practical applications:
-
Construction and Engineering: Calculating areas for flooring, wall coverings, or land plots often involves multiplications like 18 x 18. Engineers utilize these calculations to estimate material requirements.
-
Manufacturing and Design: In manufacturing, dimensions and quantities often involve multiples of 18, making 18 x 18 relevant in calculating production outputs or material needs.
-
Data Analysis and Statistics: Though indirect, the concept of squares and multiplication is fundamental to statistical calculations, such as variance and standard deviation.
-
Everyday Life: From tiling a floor to arranging objects in a grid pattern, the concept of multiplication and squares finds numerous applications in daily life. A gardener might need to calculate the area of a section of their garden that is 18 feet by 18 feet (324 sq ft).
Advanced Mathematical Concepts Related to 18 x 18
The simple calculation opens doors to understanding more complex concepts:
-
Higher-Dimensional Geometry: Extending the concept to higher dimensions (e.g., hypercubes) involves repeated multiplications.
-
Abstract Algebra: The properties of 324 can be explored within the framework of abstract algebra, examining its behavior under different group operations.
-
Number Systems: The number 324 and its prime factorization can be explored in different number systems (e.g., binary, hexadecimal).
-
Advanced Number Theory: Concepts like quadratic residues and modular forms build upon the fundamental properties of numbers like 324.
Frequently Asked Questions (FAQ)
-
What are the factors of 324? The factors of 324 are 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 81, 108, 162, and 324.
-
Is 324 a prime number? No, 324 is a composite number, meaning it has factors other than 1 and itself.
-
What is the square root of 324? The square root of 324 is 18.
-
What is the prime factorization of 324? The prime factorization of 324 is 2² x 3⁴.
-
What are some real-world applications of 18 x 18? Calculating areas (e.g., floor tiling, land measurement), volume (e.g., cubic containers), and material quantities in various fields like construction and manufacturing.
Conclusion
The seemingly simple calculation of 18 x 18 = 324 reveals a surprising depth of mathematical richness. From basic arithmetic to advanced concepts in algebra, geometry, and number theory, this equation serves as a gateway to understanding fundamental mathematical principles and their widespread applicability in various fields. Its practical implications in everyday life and various professions further highlight the importance of understanding even seemingly basic mathematical operations. By exploring this equation in detail, we not only obtain the answer but also gain a deeper appreciation for the interconnectedness of mathematical concepts and their practical relevance in the world around us. The journey from a simple multiplication problem to a comprehensive exploration of its mathematical properties and applications demonstrates the power and beauty of mathematics.
Latest Posts
Latest Posts
-
Imperialism In Spanish American War
Sep 18, 2025
-
How To Calculate Rf Chromatography
Sep 18, 2025
-
How Is A Macromolecule Formed
Sep 18, 2025
-
7 6 As A Decimal
Sep 18, 2025
-
Tabla De Conversion De Temperatura
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 1 8 X 1 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.