1 Times 1 Times 1
zacarellano
Sep 13, 2025 · 6 min read
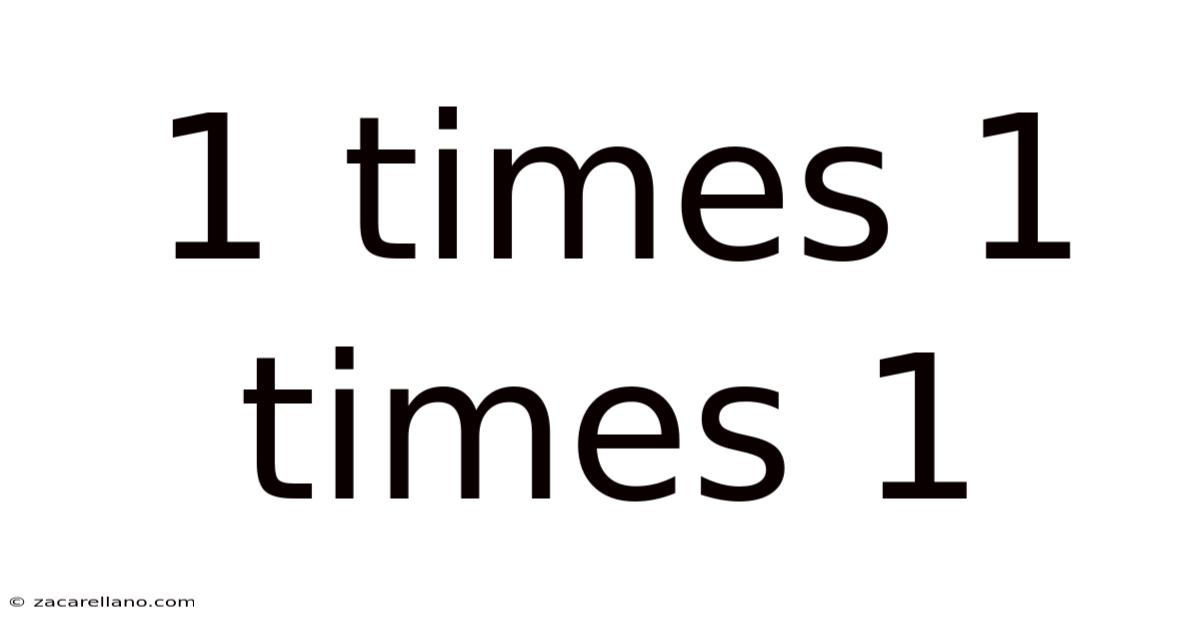
Table of Contents
Decoding the Seemingly Simple: 1 x 1 x 1 and its Implications Across Mathematics and Beyond
The seemingly trivial equation, 1 x 1 x 1, might appear to offer little to unpack. After all, the answer is undeniably 1. However, a deeper exploration reveals this simple calculation to be a gateway to understanding fundamental mathematical concepts, the nature of identity elements, and surprisingly, even philosophical considerations. This article delves into the multifaceted world of 1 x 1 x 1, uncovering its significance within arithmetic, algebra, and beyond.
Introduction: The Power of One
The number 1 holds a unique position in mathematics. It's the multiplicative identity, meaning that any number multiplied by 1 remains unchanged. This seemingly simple property underpins a vast array of mathematical operations and principles. The equation 1 x 1 x 1 perfectly exemplifies this property. Understanding this seemingly basic equation allows us to build a foundation for more complex mathematical concepts. We will explore this foundation, examining how the concept of the multiplicative identity influences various branches of mathematics and even touches upon broader philosophical questions about identity and existence.
1 x 1 x 1: A Step-by-Step Breakdown
Let's dissect the calculation itself. The expression 1 x 1 x 1 involves the operation of multiplication performed repeatedly.
-
Step 1: 1 x 1 = 1 The first multiplication results in 1. This is a direct application of the multiplicative identity. Multiplying any number by 1 yields the original number.
-
Step 2: 1 x 1 = 1 The result from Step 1 (which is 1) is then multiplied by another 1. Again, the multiplicative identity ensures the result remains 1.
-
Step 3: The Final Result The final answer, therefore, is 1.
This simple sequence clearly demonstrates the fundamental role of the multiplicative identity in mathematical operations. The consistency of the result reinforces the understanding that multiplying by 1 leaves the operand unaltered. This seemingly trivial example forms the bedrock for more advanced mathematical concepts.
The Multiplicative Identity: Its Significance in Mathematics
The multiplicative identity, represented by the number 1, plays a crucial role across various mathematical fields. It isn't just a convenient shortcut; it's a foundational element.
-
Arithmetic: As seen in our example, the multiplicative identity simplifies calculations and ensures consistency. Its application extends to more complex arithmetic involving fractions, decimals, and integers.
-
Algebra: In algebra, the multiplicative identity is essential for manipulating equations and simplifying expressions. It allows us to introduce or remove factors of 1 without altering the value of the equation. For instance, when solving for x in the equation x = 2, multiplying both sides by 1 doesn't change the solution.
-
Calculus: Even in the realm of calculus, which deals with limits, derivatives, and integrals, the multiplicative identity remains significant. It's used in simplifying expressions and proving various theorems.
-
Linear Algebra: The identity matrix, a square matrix with ones on the main diagonal and zeros elsewhere, serves as the multiplicative identity for matrix multiplication. This concept is critical in linear algebra and has broad applications in computer graphics, physics, and engineering.
-
Abstract Algebra: The concept of the multiplicative identity extends to abstract algebra, where it's generalized to the notion of an identity element within various algebraic structures like groups, rings, and fields. These structures form the basis for advanced mathematical studies.
Beyond Numbers: Philosophical Implications
While seemingly elementary, the concept of the multiplicative identity, as embodied in 1 x 1 x 1, extends beyond the purely mathematical realm. It touches upon philosophical questions of identity and existence.
-
Identity and Change: The number 1, in its unchanging nature when multiplied by itself, can be seen as a metaphor for identity amidst change. It represents something that remains constant even when subjected to an operation. This concept resonates with philosophical discussions of personal identity and the permanence of the self.
-
Existence and Non-Existence: The number 1 can be interpreted as representing existence – a single entity. The equation 1 x 1 x 1 could then be seen as a representation of the continuation of existence, with each multiplication representing a point in time. This provides a simple, albeit abstract, analogy for the continuity of being.
-
The Paradox of Self-Replication: The equation 1 x 1 x 1 can be viewed as a symbolic representation of self-replication. Each 1 replicates itself, resulting in the same entity. This ties into philosophical discussions surrounding self-replication in nature and artificial intelligence.
1 x 1 x 1 in Different Number Systems
The simplicity of 1 x 1 x 1 remains consistent even when we consider different number systems.
-
Binary System: In the binary system (base-2), 1 is still the multiplicative identity. 1 x 1 x 1 in binary is still equal to 1.
-
Hexadecimal System: Similarly, in the hexadecimal system (base-16), the multiplicative identity is still represented by 1, and 1 x 1 x 1 remains 1.
This consistency across different number systems highlights the universality of the multiplicative identity and its fundamental importance in mathematics.
Addressing Common Questions (FAQ)
Q1: Is there any practical application of 1 x 1 x 1 beyond basic arithmetic?
A1: While 1 x 1 x 1 itself is a simple calculation, the underlying principle – the multiplicative identity – is crucial in countless applications. It's fundamental to computer programming, engineering calculations, and various scientific models.
Q2: Can this equation be expanded to include more 1s?
A2: Yes, the equation can be expanded indefinitely. 1 x 1 x 1 x 1... (n times) will always equal 1. This underscores the unchanging nature of the multiplicative identity.
Q3: Are there any instances where 1 is not the multiplicative identity?
A3: In most standard mathematical systems, 1 is consistently the multiplicative identity. However, in certain specialized mathematical structures or unconventional systems, it might be different. Understanding such exceptions requires a more advanced grasp of abstract algebra.
Q4: What about 0 x 0 x 0? Is it similar?
A4: 0 x 0 x 0 is different. 0 is the additive identity (adding 0 doesn't change the number). However, 0 multiplied by itself any number of times always results in 0. This highlights the crucial distinction between additive and multiplicative identities.
Conclusion: The Enduring Significance of Simplicity
The equation 1 x 1 x 1, while appearing trivial at first glance, unveils a profound depth when examined closely. It serves as a gateway to understanding the fundamental concept of the multiplicative identity, a crucial element in numerous mathematical branches and even philosophical considerations. Its simplicity belies its importance, highlighting how basic principles can underpin complex systems and concepts. From simple arithmetic to abstract algebra and even philosophical interpretations, the exploration of 1 x 1 x 1 underscores the richness and interconnectedness of mathematical ideas and their implications far beyond the realm of numbers themselves. The enduring power of this seemingly simple equation lies in its ability to illuminate the fundamental building blocks of mathematics and spark broader intellectual curiosity.
Latest Posts
Latest Posts
-
Z Score To Percentile Table
Sep 14, 2025
-
First Vs Second Great Awakening
Sep 14, 2025
-
Math Notes For 5th Graders
Sep 14, 2025
-
Ap Physics 1 Unit 3
Sep 14, 2025
-
Types Of Collisions In Physics
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 1 Times 1 Times 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.