10 Divided By 4 5
zacarellano
Sep 20, 2025 · 5 min read
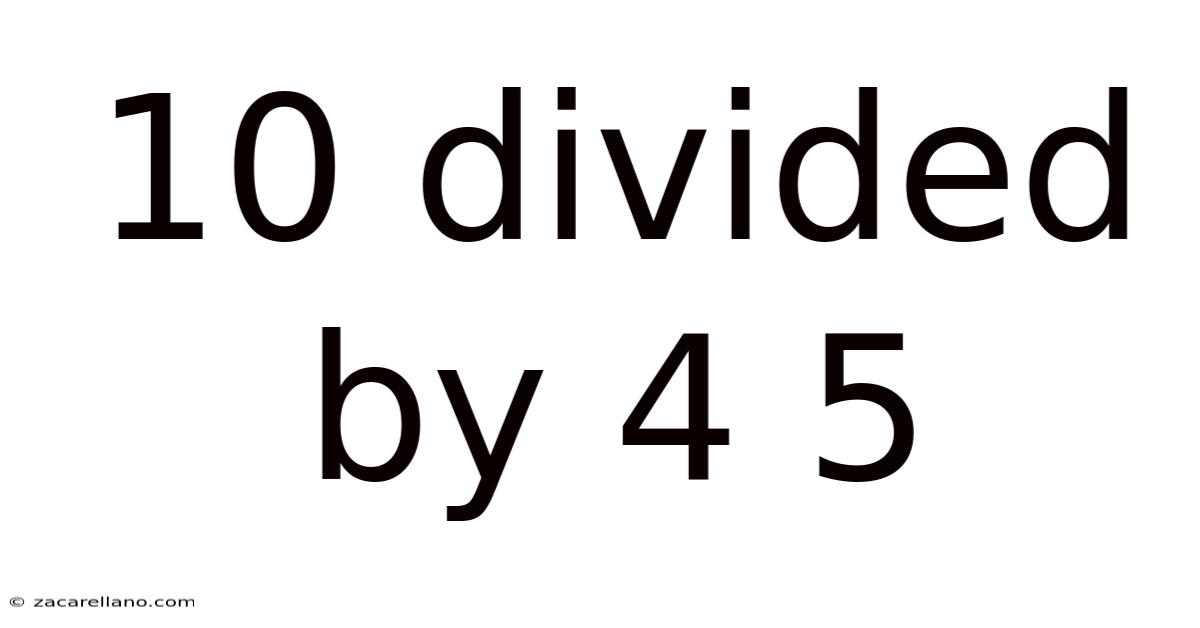
Table of Contents
Unveiling the Mystery: 10 Divided by 4.5 (A Deep Dive into Division)
The seemingly simple question, "What is 10 divided by 4.5?", opens a door to a deeper understanding of division, decimal numbers, and practical applications in various fields. This article will not only provide the answer but also explore the underlying principles, different methods for solving the problem, and real-world scenarios where such calculations are crucial. We'll cover various approaches, from basic long division to using calculators and understanding the concept of reciprocals, ensuring a thorough comprehension for readers of all mathematical backgrounds.
Understanding Division: The Basics
Before we tackle 10 divided by 4.5, let's refresh our understanding of division. Division is essentially the inverse operation of multiplication. When we divide a number (the dividend) by another number (the divisor), we're essentially finding out how many times the divisor fits into the dividend. For example, 10 ÷ 2 = 5 means that the number 2 fits into 10 five times.
This fundamental concept extends to scenarios involving decimal numbers, like our problem of 10 ÷ 4.5. While it might seem more complex initially, the underlying principle remains the same: we are searching for how many times 4.5 fits into 10.
Method 1: Long Division
One traditional method for solving this is long division. However, dividing by a decimal can be tricky. To simplify, we can eliminate the decimal in the divisor by multiplying both the dividend and the divisor by a power of 10. In this case, multiplying both by 10 will eliminate the decimal point in 4.5:
10 × 10 = 100 4.5 × 10 = 45
Now, our problem becomes 100 ÷ 45. Let's perform long division:
2
45 | 100
-90
10
The result shows that 45 goes into 100 two times with a remainder of 10. To express the remainder as a decimal, we can add a decimal point and a zero to the dividend and continue the division:
2.222...
45 | 100.000
-90
100
-90
100
-90
100
...
This shows that the division results in a repeating decimal, approximately 2.222... We can round this to a desired level of accuracy, for example, 2.22.
Method 2: Using Fractions
Another approach is to convert the division problem into a fraction:
10 ÷ 4.5 = 10/4.5
To simplify this fraction, we can again multiply both the numerator and the denominator by 10 to remove the decimal:
(10 × 10) / (4.5 × 10) = 100/45
Now, we can simplify this fraction by finding the greatest common divisor (GCD) of 100 and 45, which is 5:
100 ÷ 5 = 20 45 ÷ 5 = 9
Therefore, the simplified fraction is 20/9. To convert this fraction to a decimal, we perform the division:
20 ÷ 9 = 2.222...
Again, we obtain the repeating decimal 2.222..., which can be rounded to a desired level of accuracy.
Method 3: Using a Calculator
The simplest and often quickest method is using a calculator. Simply enter 10 ÷ 4.5 and the calculator will provide the answer, likely displaying it as 2.222... or a similar rounded value.
Understanding Repeating Decimals
The result of 10 ÷ 4.5, 2.222..., is a repeating decimal. This means the digit 2 repeats infinitely. Repeating decimals are often represented using a bar over the repeating digits, like this: 2.2̅. These numbers are rational numbers, meaning they can be expressed as a fraction (in this case, 20/9).
Real-World Applications
Understanding division involving decimal numbers is vital in numerous real-world scenarios:
-
Finance: Calculating unit costs, determining profit margins, and dividing expenses are common applications. For example, if you have $10 and need to buy items costing $4.5 each, you can determine how many you can afford.
-
Engineering: In engineering design, precise calculations are essential, often involving decimal numbers and divisions. This could include calculating material quantities, dimensions, or power distribution.
-
Cooking and Baking: Scaling recipes up or down frequently involves dividing ingredients by decimal values. If a recipe calls for 4.5 cups of flour and you want to halve it, you'll need to calculate 4.5 ÷ 2.
-
Science: Scientific measurements often result in decimal numbers, and analyzing data frequently requires division operations. This can be seen in fields such as chemistry, physics, and biology.
Further Exploration: Reciprocals
Understanding reciprocals can further illuminate the process of division. The reciprocal of a number is simply 1 divided by that number. For instance, the reciprocal of 4.5 is 1/4.5 = 0.222...
When dividing by a number, you can equivalently multiply by its reciprocal. Therefore, 10 ÷ 4.5 is the same as 10 × (1/4.5) = 10 × 0.222... ≈ 2.222...
Frequently Asked Questions (FAQ)
-
Q: Why does 10 divided by 4.5 result in a repeating decimal? A: Because the fraction 20/9, which is equivalent to 10/4.5, cannot be simplified to a fraction with a denominator that is a power of 10. This means its decimal representation will be non-terminating (it goes on forever) and repeating.
-
Q: Can I use a different method to solve this problem? A: Yes, you can use various methods. Long division, converting to fractions, and using a calculator are all viable approaches. The choice often depends on personal preference, the tools available, and the desired level of accuracy.
-
Q: Is it necessary to show all the repeating digits? A: No, usually rounding to a reasonable number of decimal places is sufficient. The level of accuracy needed depends on the context of the problem. For many practical applications, rounding to two or three decimal places is more than adequate.
-
Q: What if I have a more complex division problem with decimals? A: The principles remain the same. You can use the same techniques: eliminate decimal points by multiplying by powers of 10, convert to fractions, or use a calculator. Long division might become more cumbersome for complex problems, making a calculator the preferred method.
Conclusion
The seemingly simple problem of 10 divided by 4.5 provides a rich opportunity to explore fundamental mathematical concepts. This article has demonstrated various methods for solving the problem, highlighting the importance of understanding long division, fractions, and the nature of repeating decimals. By grasping these concepts, you'll be well-equipped to tackle similar problems and appreciate the practical applications of division in various fields. Remember, the key is to choose the method that best suits your needs and always strive for clear and accurate understanding. The answer, approximately 2.22, is just the beginning of a deeper mathematical journey.
Latest Posts
Latest Posts
-
Newtons Second Law Practice Problems
Sep 20, 2025
-
Japan In The Middle Ages
Sep 20, 2025
-
16 Oz Pasta To Lbs
Sep 20, 2025
-
Online Learning For 3rd Graders
Sep 20, 2025
-
What Is The 10 Condition
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 10 Divided By 4 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.