10 X 10 X 100
zacarellano
Sep 20, 2025 · 6 min read
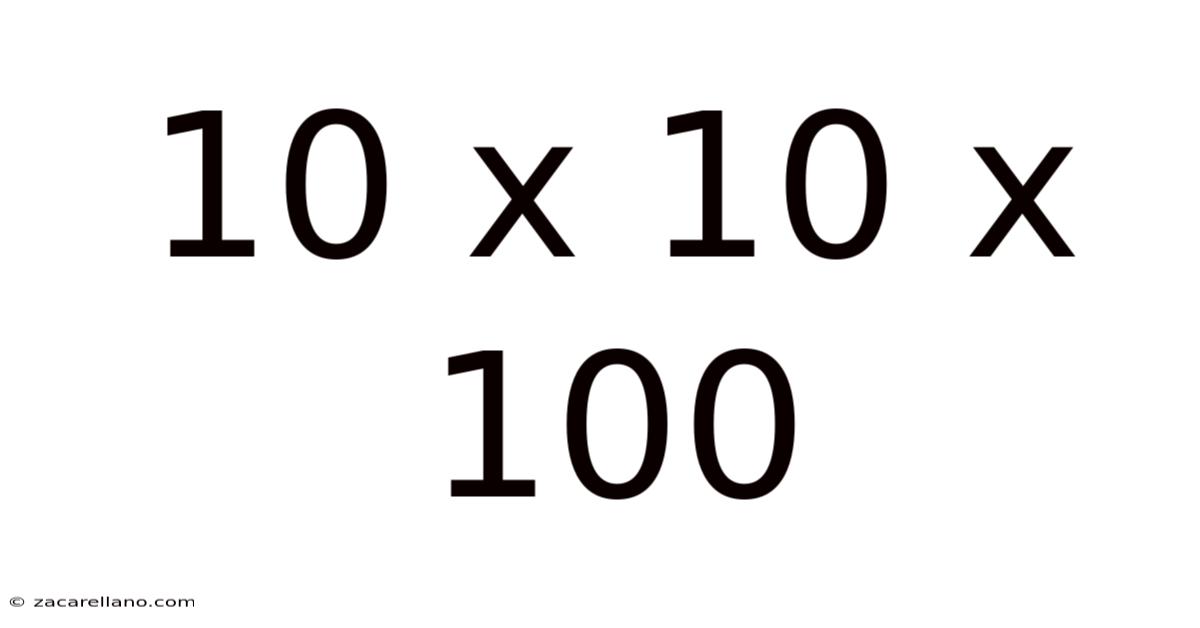
Table of Contents
Exploring the Intriguing World of 10 x 10 x 100: A Deep Dive into Mathematics, Applications, and Conceptual Understanding
The seemingly simple expression "10 x 10 x 100" offers a fascinating gateway into various mathematical concepts and real-world applications. This article delves deep into the numerical value, explores its implications across different fields, and unpacks the underlying principles to foster a comprehensive understanding, suitable for learners of all backgrounds. We'll move beyond the basic calculation to uncover the richness and versatility embedded within this seemingly straightforward equation.
I. The Fundamental Calculation and its Result
At its core, "10 x 10 x 100" is a straightforward multiplication problem. Following the order of operations (multiplication from left to right), the calculation proceeds as follows:
- 10 x 10 = 100
- 100 x 100 = 10,000
Therefore, the solution to 10 x 10 x 100 is 10,000. This seemingly simple result serves as a foundation for exploring more complex ideas and applications.
II. Understanding the Power of Exponents
The expression 10 x 10 x 100 can also be represented using exponents. We can rewrite 10 x 10 as 10², meaning 10 raised to the power of 2. Then, the equation becomes:
10² x 10² = 10⁴
This demonstrates the fundamental principle of exponent rules: when multiplying numbers with the same base (in this case, 10), you add the exponents. Understanding exponents is crucial for working with larger numbers and solving more complex mathematical problems. This concept is vital in various fields like computer science, physics, and finance where exponential growth or decay are common occurrences.
III. Exploring Applications in Different Fields
The number 10,000, the result of our calculation, finds applications across numerous disciplines. Let's explore a few:
-
Finance: 10,000 can represent a significant monetary amount. It might be a down payment on a house, a savings goal, or a significant investment. Understanding the principles of compound interest, closely related to exponents, is crucial for managing such financial quantities. Calculating compound interest involves repeated multiplication, similar to the repeated multiplication seen in our original expression.
-
Measurement and Units: The metric system, widely used globally, is based on powers of 10. 10,000 centimeters equals 100 meters, showcasing the interconnectedness of units within the metric system. This demonstrates the practical relevance of understanding multiples of 10 in measurements and conversions.
-
Computer Science: In binary systems (the foundation of computer operations), while not directly represented as 10,000, the underlying principles of base-10 arithmetic and exponential growth are pivotal. The way computers process and store information relies heavily on binary numbers, which are directly related to powers of 2, conceptually similar to the power of 10 we've explored. Memory allocation, data structures, and algorithmic efficiency all depend on understanding exponential relationships.
-
Engineering and Design: Engineers often work with large quantities and precise measurements. 10,000 might represent a number of units produced, a specific dimension in a design, or a load capacity in structural engineering. Understanding the numerical relationships and scales of measurement is essential for accurate design and efficient project management.
-
Population Studies: In demographics, 10,000 might represent a significant population size for a particular community or a specific demographic group. Analyzing population trends often involves exponential growth or decay models, directly relevant to the exponential concepts explored above.
IV. Beyond the Calculation: Developing Mathematical Intuition
While the solution to 10 x 10 x 100 is easily calculated, the true value lies in understanding the underlying mathematical principles. This problem offers an opportunity to develop:
-
Number Sense: Repeated practice with such calculations improves our ability to quickly estimate and approximate results, strengthening our overall number sense. Being able to quickly grasp the magnitude of numbers is vital in various aspects of life, from budgeting to problem-solving.
-
Problem-Solving Skills: Breaking down complex problems into smaller, manageable steps, as we did with the multiplication, is a crucial problem-solving skill applicable across many fields. This approach enhances critical thinking and analytical abilities.
-
Pattern Recognition: The relationship between 10, 100, and 10,000 illustrates the pattern of powers of 10. Recognizing patterns helps us predict outcomes and develop a deeper understanding of mathematical relationships. This pattern recognition is not only important in mathematics but also in other areas like science, where identifying trends is crucial for drawing conclusions.
V. Expanding the Concept: Variations and Extensions
Let's explore some variations of the original problem to further enhance our understanding:
-
10 x 10 x 10 x 100: This extends the problem by adding another factor of 10, resulting in 100,000. This expands our exploration of exponents and their application to larger numbers.
-
10 x 10 x x: This introduces an unknown variable 'x', transforming the problem into an algebraic equation. Solving for 'x' in different scenarios will hone our skills in algebra and equation solving.
-
(10 + 10) x (10 + 10) x 100: This variation introduces parentheses, emphasizing the importance of the order of operations in mathematics. Solving this correctly requires a proper understanding of BODMAS/PEMDAS.
VI. Frequently Asked Questions (FAQ)
-
Q: What are some real-world scenarios where this calculation might be used? A: As discussed earlier, calculating areas, volumes, financial projections, and analyzing population trends are just some examples. The calculation becomes a building block for many more complex calculations.
-
Q: How does this relate to scientific notation? A: The result, 10,000, can be expressed in scientific notation as 1 x 10⁴, emphasizing the power of 10 as a base for scientific measurements.
-
Q: Why is understanding exponents important? A: Exponents allow us to represent extremely large or small numbers concisely and efficiently. They are fundamental for understanding exponential growth and decay, critical in various scientific and financial models.
-
Q: Can this problem be solved using a calculator? A: Yes, a simple calculator can be used to verify the result quickly. However, understanding the underlying mathematical processes is more important than just obtaining the numerical answer.
VII. Conclusion: The Value Beyond the Numbers
The seemingly simple expression "10 x 10 x 100" offers far more than just a numerical answer. It provides a springboard to explore fundamental mathematical concepts, develop problem-solving skills, and understand the real-world applications of these principles across diverse fields. By delving into the details, we not only find the solution but also cultivate a deeper appreciation for the beauty and practical utility of mathematics. The journey from a simple calculation to a comprehensive understanding exemplifies the enriching process of mathematical exploration, fostering critical thinking and a nuanced appreciation for the power of numbers. The exploration continues beyond the confines of this article, encouraging further investigation and application of these mathematical principles in your own learning and endeavors.
Latest Posts
Latest Posts
-
The Gains From Trade Are
Sep 20, 2025
-
Valence Electrons Of The Elements
Sep 20, 2025
-
Oath Of The Horatii Composition
Sep 20, 2025
-
Calvin Cycle A Level Biology
Sep 20, 2025
-
Carbon Chains Kids Picture Scientist
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 10 X 10 X 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.