15 Divided By 2 3
zacarellano
Sep 16, 2025 · 6 min read
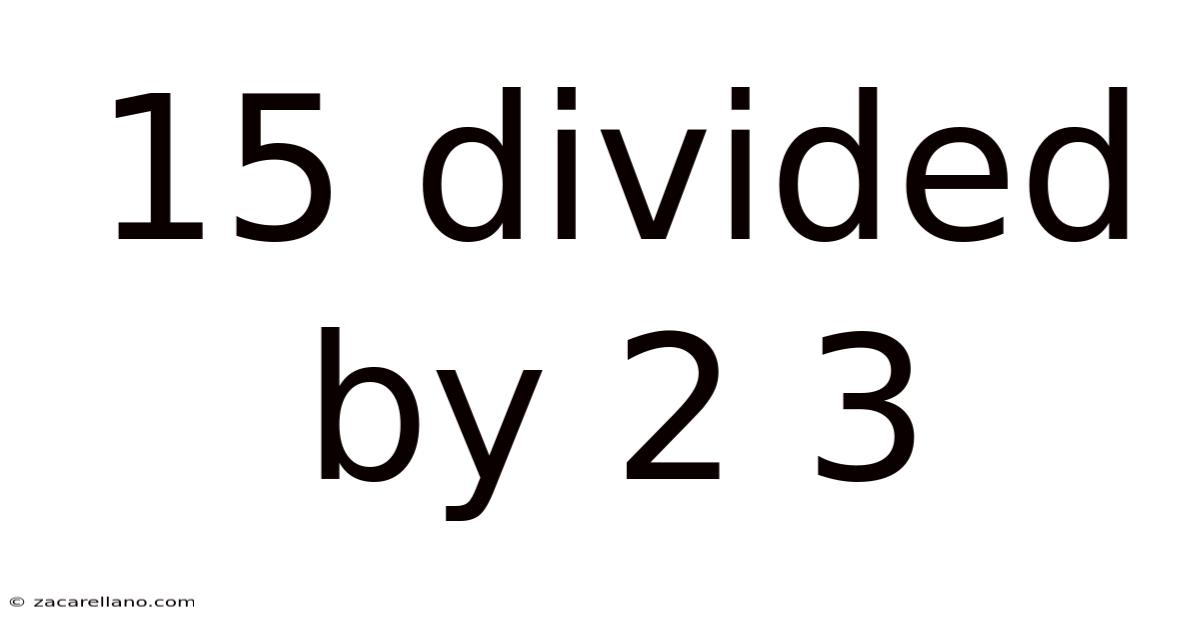
Table of Contents
Unpacking the Mystery: 15 Divided by 2/3
This article explores the seemingly simple, yet often confusing, mathematical problem of 15 divided by 2/3. We'll break down the process step-by-step, providing a clear understanding of the underlying principles and offering various approaches to solve this common fraction division problem. Understanding this concept is crucial for anyone studying arithmetic, algebra, and beyond. This guide provides a comprehensive explanation suitable for students of all levels, from elementary school to high school. We'll also delve into the mathematical reasoning behind the solution and address frequently asked questions.
Understanding Fraction Division: The Basics
Before diving into the specific problem of 15 divided by 2/3, let's establish a solid foundation in fraction division. The key concept to remember is that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2.
This seemingly simple rule significantly simplifies fraction division. Instead of grappling with the complexities of directly dividing by a fraction, we can convert the problem into a much easier multiplication problem. This transformation is the core of efficiently solving problems like 15 divided by 2/3.
Method 1: Converting to Improper Fractions and Multiplying
This method is a classic approach and is often taught in elementary and middle school mathematics. It involves two key steps:
-
Rewrite the whole number as a fraction: The whole number 15 can be written as the fraction 15/1. This step makes the problem consistent, allowing us to apply the rules of fraction division uniformly.
-
Multiply by the reciprocal: Now, instead of 15/1 divided by 2/3, we'll multiply 15/1 by the reciprocal of 2/3, which is 3/2. Our equation now looks like this: (15/1) * (3/2).
-
Perform the multiplication: Multiply the numerators (top numbers) together and the denominators (bottom numbers) together: (15 * 3) / (1 * 2) = 45/2.
-
Simplify the Result: The fraction 45/2 is an improper fraction (the numerator is larger than the denominator). To express this as a mixed number (a whole number and a fraction), we divide 45 by 2. This gives us 22 with a remainder of 1. Therefore, 45/2 is equivalent to 22 1/2.
Therefore, 15 divided by 2/3 equals 22 1/2.
Method 2: Using the "Keep, Change, Flip" Method
This method provides a more intuitive way to remember the process of dividing fractions. The mnemonic "Keep, Change, Flip" simplifies the steps:
-
Keep: Keep the first number (15/1) exactly as it is.
-
Change: Change the division sign (÷) to a multiplication sign (×).
-
Flip: Flip the second fraction (2/3) to its reciprocal (3/2).
This transforms the problem from (15/1) ÷ (2/3) to (15/1) × (3/2). From here, you follow the same multiplication steps as in Method 1 to arrive at the answer of 22 1/2. This method is particularly useful for visualizing the process and helps students remember the crucial step of using the reciprocal.
Method 3: Visual Representation
While the previous methods are mathematically precise, a visual approach can provide a deeper understanding, especially for visual learners. Imagine you have 15 whole units (e.g., pizzas). You want to divide these 15 units into portions that are each 2/3 of a unit. How many 2/3 portions can you make?
To solve this visually, consider that one whole unit contains three 1/3 portions. Therefore, 15 whole units contain 15 * 3 = 45 portions of 1/3. Since we’re looking for portions that are 2/3, we divide the total number of 1/3 portions (45) by 2: 45 / 2 = 22.5. This confirms our earlier answer of 22 1/2. This visual method emphasizes the practical application of the problem, helping to solidify the abstract concept.
The Mathematical Rationale: Why Does This Work?
The fundamental principle behind dividing by a fraction is rooted in the concept of reciprocals and the multiplicative inverse. Every non-zero number has a multiplicative inverse, which, when multiplied by the original number, results in 1. The reciprocal of a fraction is its multiplicative inverse.
When we divide by a fraction (a/b), we're essentially asking, "How many times does (a/b) fit into the number we're dividing?" Multiplying by the reciprocal (b/a) is a mathematical shortcut to answer this question. It transforms the division problem into a multiplication problem that yields the same result, making the calculation significantly easier. This underlying principle connects directly to the algebra concept of inverse operations.
Addressing Common Mistakes
A common mistake when dividing fractions is forgetting to use the reciprocal. Students might inadvertently multiply by the original fraction, leading to an incorrect answer. Remember the crucial steps: convert whole numbers into fractions, and then always multiply by the reciprocal of the divisor (the number you're dividing by).
Another common error is incorrectly simplifying the resulting fraction. Always ensure that the final fraction is in its simplest form. This involves finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by the GCD.
Frequently Asked Questions (FAQ)
-
Q: Can I solve this using decimals?
A: Yes, you can convert the fraction 2/3 to its decimal equivalent (approximately 0.6667) and then perform the division using a calculator. However, this approach might introduce rounding errors, leading to a slightly less precise answer compared to using fractions.
-
Q: What if the problem was 15 divided by 3/2?
A: The process remains the same. You would rewrite 15 as 15/1, change the division to multiplication, and flip 3/2 to its reciprocal (2/3). The equation becomes (15/1) × (2/3) = 10.
-
Q: Why is it important to understand fraction division?
A: Understanding fraction division is crucial for a solid foundation in mathematics. It’s fundamental to more advanced concepts in algebra, calculus, and other areas of mathematics and science. Many real-world applications, from cooking recipes to construction projects, involve working with fractions and proportions.
-
Q: Are there other methods to solve this type of problem?
A: While the methods described above are the most common and widely used, there are alternative approaches involving long division with fractions or using visual models that break down the problem into smaller, manageable parts. These methods, although effective, might be less efficient than the ones discussed.
Conclusion: Mastering Fraction Division
This article provided a comprehensive exploration of solving the problem 15 divided by 2/3. We've examined multiple methods, highlighting their underlying principles, and addressed common mistakes. By understanding the concept of reciprocals and applying the "Keep, Change, Flip" method or the improper fraction method, you can confidently tackle similar fraction division problems. Remember to practice regularly to solidify your understanding and build confidence in your mathematical abilities. Mastering fraction division is a crucial step towards a stronger foundation in mathematics, opening doors to more advanced concepts and real-world applications. Through consistent practice and a clear grasp of the underlying principles, you can confidently navigate the world of fractions and unlock their full potential.
Latest Posts
Latest Posts
-
Signo De Mayo Y Menor
Sep 16, 2025
-
Naming And Writing Ionic Formulas
Sep 16, 2025
-
What Is Kw Of Water
Sep 16, 2025
-
Silica Gel Thin Layer Chromatography
Sep 16, 2025
-
What Is A Column Space
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 15 Divided By 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.