18 Percent In Decimal Form
zacarellano
Sep 13, 2025 · 5 min read
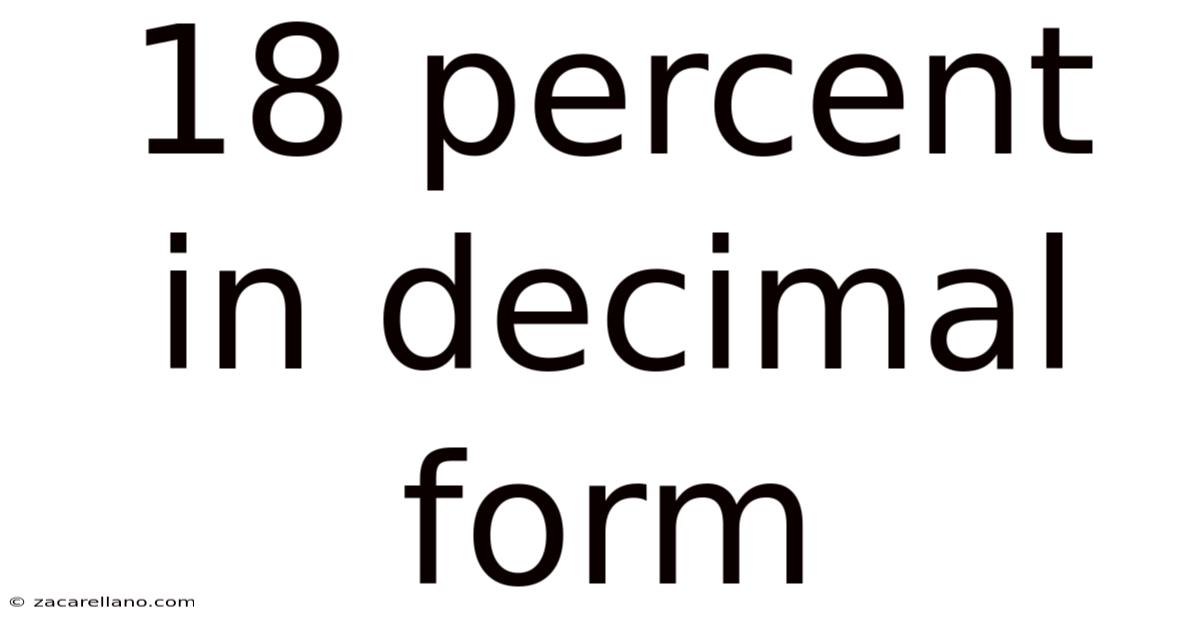
Table of Contents
18 Percent in Decimal Form: A Comprehensive Guide
Understanding percentages and their decimal equivalents is fundamental to various aspects of life, from calculating discounts and interest rates to comprehending statistical data and analyzing financial reports. This comprehensive guide will delve into the conversion of 18 percent to its decimal form, exploring the underlying principles and offering practical applications. We'll move beyond the simple conversion and explore related concepts to solidify your understanding. This will enable you to confidently tackle percentage-related problems in any context.
Understanding Percentages
Before jumping into the conversion of 18%, let's briefly review the concept of percentages. A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin phrase "per centum," meaning "out of one hundred." Therefore, 18% means 18 out of 100, or 18/100.
Converting 18 Percent to Decimal Form
Converting a percentage to its decimal equivalent is a straightforward process. The key is to remember that the percentage symbol (%) represents division by 100. To convert 18% to a decimal, we simply divide 18 by 100:
18% = 18/100 = 0.18
Therefore, 18 percent in decimal form is 0.18.
The Underlying Mathematics: Understanding Decimal Places
The decimal system is based on powers of 10. Each place value to the right of the decimal point represents a decreasing power of 10: tenths (1/10), hundredths (1/100), thousandths (1/1000), and so on. When we divide 18 by 100, we are essentially placing the number 18 in the hundredths place.
Practical Applications of 18% and its Decimal Equivalent (0.18)
The decimal form of 18% (0.18) has numerous practical applications across various fields:
-
Finance: Calculating interest rates, discounts, taxes, and profit margins often involves using percentages and their decimal equivalents. For instance, if a bank offers an 18% annual interest rate on a savings account, you would use 0.18 to calculate the interest earned.
-
Statistics: Percentages and decimals are essential for representing and analyzing data. For example, if 18% of respondents in a survey chose a particular option, this would be represented as 0.18 in statistical calculations.
-
Business: Businesses utilize percentages and decimals in areas such as sales, cost analysis, and pricing strategies. An 18% discount on an item would be calculated using the decimal 0.18.
-
Everyday Life: We encounter percentages and their decimal equivalents in our daily lives in various situations, such as calculating tips, understanding sales tax, or interpreting nutritional information on food labels.
-
Science and Engineering: In scientific and engineering calculations, percentages and their decimal equivalents are often used to represent proportions, concentrations, and errors.
Beyond the Basics: Working with Percentages and Decimals
While converting 18% to 0.18 is a simple process, a strong grasp of percentage and decimal manipulation is crucial for solving more complex problems. Here are some essential skills to develop:
-
Converting Decimals to Percentages: The reverse process – converting a decimal to a percentage – involves multiplying the decimal by 100 and adding the percentage symbol. For example, 0.35 is equivalent to 35%.
-
Calculating Percentages of Numbers: To find a percentage of a number, convert the percentage to a decimal and then multiply the decimal by the number. For instance, 18% of 500 is calculated as 0.18 * 500 = 90.
-
Finding the Percentage Increase or Decrease: This involves calculating the difference between two numbers, dividing the difference by the original number, and then multiplying the result by 100 to express it as a percentage.
-
Working with Compound Interest: Compound interest calculations involve repeatedly applying an interest rate over time, requiring a strong understanding of percentage and decimal manipulation.
Illustrative Examples: Applying 18% in Different Contexts
Let’s illustrate the application of 18% and its decimal equivalent (0.18) with a few examples:
Example 1: Sales Discount
A store offers an 18% discount on a $100 item. To calculate the discount amount, we multiply the price by the decimal equivalent of 18%:
Discount = 0.18 * $100 = $18
The discounted price is $100 - $18 = $82
Example 2: Sales Tax
If the sales tax in a region is 18%, and you buy an item costing $50, the sales tax amount is calculated as:
Sales Tax = 0.18 * $50 = $9
The total cost including tax is $50 + $9 = $59
Example 3: Interest Calculation
Suppose you invest $1000 in a savings account that offers an 18% annual interest rate. After one year, the interest earned would be:
Interest = 0.18 * $1000 = $180
Your total balance after one year would be $1000 + $180 = $1180. Note that this is simple interest. Compound interest calculations would be more complex.
Frequently Asked Questions (FAQ)
Q1: What is the easiest way to remember how to convert a percentage to a decimal?
A1: The simplest method is to remember that the percentage symbol (%) means "divide by 100." Just move the decimal point two places to the left.
Q2: Can I convert any percentage to a decimal using this method?
A2: Yes, this method works for all percentages. For instance, 5% becomes 0.05, 100% becomes 1.00, and 250% becomes 2.50.
Q3: What if the percentage involves a fraction, such as 18 1/2%?
A3: First, convert the mixed fraction to a decimal. 18 1/2% is equal to 18.5%. Then, divide by 100 to get the decimal equivalent: 18.5/100 = 0.185.
Q4: Are there any other methods to convert percentages to decimals?
A4: Yes, you can also use a calculator or spreadsheet software to perform the division directly. Many calculators have a percentage button (%) that simplifies the conversion.
Conclusion
Converting 18% to its decimal form (0.18) is a fundamental skill with wide-ranging applications. Understanding the underlying principles of percentages and decimals empowers you to solve problems related to finance, statistics, business, and everyday life. This guide has provided not only the answer to the core question but also the broader context, equipping you with the tools and knowledge to confidently tackle any percentage-related calculations you may encounter. Remember the simple rule: divide by 100 to convert a percentage to a decimal, and multiply by 100 to do the reverse. Mastering this skill will significantly enhance your mathematical proficiency and problem-solving abilities.
Latest Posts
Latest Posts
-
Ap Physics 1 Sample Test
Sep 13, 2025
-
Is 1000 Ml 1 Liter
Sep 13, 2025
-
Digital Sat Hard Math Questions
Sep 13, 2025
-
4th Grade Math Standards Nc
Sep 13, 2025
-
Chain Rule On Trig Functions
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 18 Percent In Decimal Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.