2 4 As A Decimal
zacarellano
Sep 06, 2025 · 5 min read
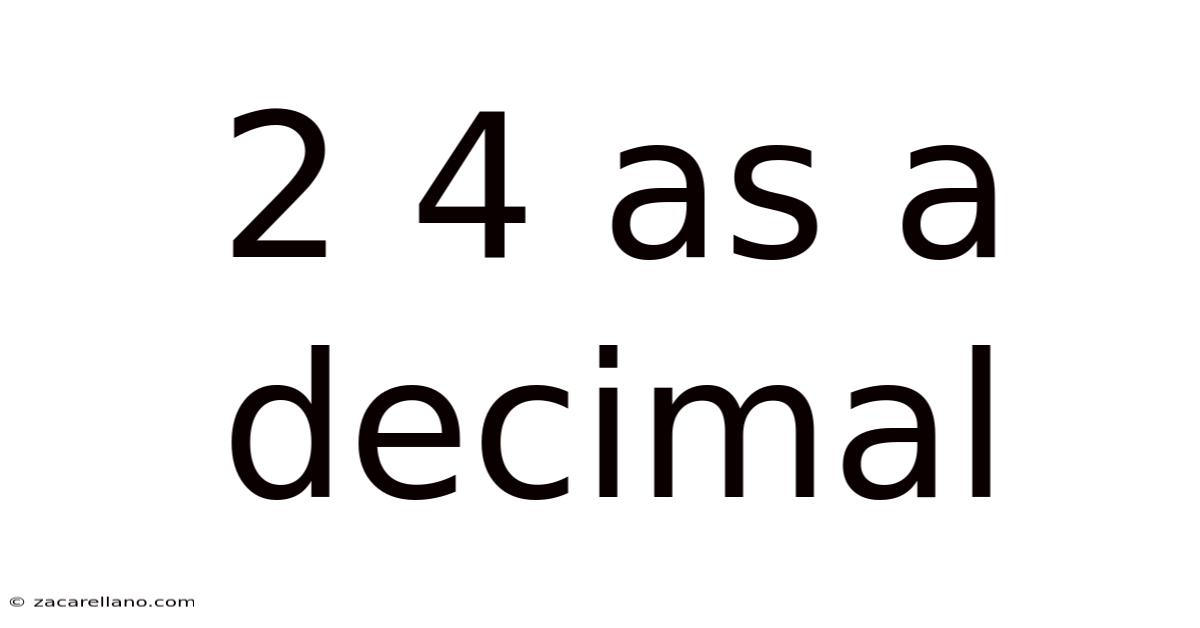
Table of Contents
Understanding 2/4 as a Decimal: A Comprehensive Guide
The seemingly simple fraction 2/4 often presents a gateway to understanding more complex concepts in mathematics, particularly the conversion between fractions and decimals. This article provides a comprehensive guide to converting 2/4 to its decimal equivalent, exploring the underlying principles, practical applications, and related mathematical concepts. We will cover various methods for the conversion, addressing potential questions and misconceptions along the way. Understanding this seemingly basic conversion forms a crucial foundation for more advanced mathematical skills.
Introduction to Fractions and Decimals
Before diving into the conversion of 2/4 to a decimal, let's briefly review the fundamental concepts of fractions and decimals.
A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 2/4, 2 is the numerator and 4 is the denominator. This means we have 2 parts out of a total of 4 equal parts.
A decimal, on the other hand, represents a fraction where the denominator is a power of 10 (10, 100, 1000, and so on). Decimals use a decimal point (.) to separate the whole number part from the fractional part. For instance, 0.5 represents 5/10, and 0.25 represents 25/100.
Method 1: Simplifying the Fraction
The simplest and most intuitive method to convert 2/4 to a decimal involves simplifying the fraction first. Observe that both the numerator (2) and the denominator (4) are divisible by 2. Therefore, we can simplify the fraction:
2/4 = (2 ÷ 2) / (4 ÷ 2) = 1/2
Now, converting 1/2 to a decimal is straightforward. Remember that a fraction represents division. So, 1/2 means 1 divided by 2:
1 ÷ 2 = 0.5
Therefore, 2/4, when simplified, is equivalent to 0.5 as a decimal.
Method 2: Direct Division
Alternatively, you can convert 2/4 to a decimal directly by performing the division without simplifying the fraction first. This method involves dividing the numerator (2) by the denominator (4):
2 ÷ 4 = 0.5
This directly yields the decimal equivalent of 0.5. This method demonstrates that simplifying the fraction beforehand is not always necessary, although it often simplifies the division process.
Method 3: Converting to a Power of 10
Another approach involves converting the fraction to an equivalent fraction with a denominator that is a power of 10. While not the most efficient method for 2/4, it illustrates a broader technique applicable to other fractions. Since 4 is not a factor of 10, 100, 1000, etc., we need to find an equivalent fraction. In this case, we already simplified 2/4 to 1/2. We can then convert 1/2 to a decimal by finding an equivalent fraction with a denominator of 10:
1/2 = (1 × 5) / (2 × 5) = 5/10
Now, 5/10 can be easily expressed as a decimal:
5/10 = 0.5
Understanding the Decimal Value: 0.5
The decimal value 0.5 represents half or 50%. It signifies that we have 5 tenths of a whole unit. This is visually represented as half of a whole. This understanding is vital for interpreting the results and applying them in various contexts.
Practical Applications of Decimal Conversion
The conversion of fractions to decimals finds applications in numerous fields, including:
- Finance: Calculating percentages, interest rates, and proportions of investments.
- Engineering: Precise measurements and calculations involving fractions of units (e.g., inches, centimeters).
- Science: Representing experimental data, analyzing proportions, and performing calculations involving ratios.
- Everyday Life: Dividing quantities, sharing resources, and understanding proportions in recipes or measurements.
Addressing Common Misconceptions
-
Improper Fractions: Some students might struggle with improper fractions (where the numerator is greater than the denominator). Remember that an improper fraction simply represents a value greater than 1. When converting an improper fraction to a decimal, perform the division as usual; the result will be a decimal greater than 1.
-
Recurring Decimals: Not all fractions convert to terminating decimals (decimals with a finite number of digits). Some fractions result in recurring or repeating decimals (decimals with a pattern of digits that repeat indefinitely). For example, 1/3 converts to 0.333...
-
Approximations: When dealing with recurring decimals, we often use approximations for practical purposes. For example, we might approximate 1/3 as 0.33 or 0.333 depending on the level of precision required.
Frequently Asked Questions (FAQ)
-
Q: Can I convert any fraction to a decimal? A: Yes, every fraction can be converted to a decimal by dividing the numerator by the denominator. The result might be a terminating decimal or a recurring decimal.
-
Q: Is simplifying the fraction necessary before conversion? A: Simplifying the fraction is not strictly necessary, but it often makes the division easier and less prone to errors.
-
Q: What if the decimal has many digits after the decimal point? A: The number of digits after the decimal point depends on the fraction. Some fractions result in terminating decimals (e.g., 1/2 = 0.5), while others result in recurring decimals (e.g., 1/3 = 0.333...). You can round the decimal to a desired level of precision as needed.
-
Q: How do I convert a decimal back to a fraction? A: To convert a decimal to a fraction, express the decimal as a fraction with a power of 10 as the denominator. Then, simplify the fraction to its lowest terms. For example, 0.75 = 75/100 = 3/4.
Conclusion
Converting 2/4 to its decimal equivalent, 0.5, highlights the fundamental relationship between fractions and decimals. Understanding this conversion is crucial for developing a solid foundation in mathematics. By mastering different methods—simplifying the fraction, direct division, and conversion to a power of 10—you gain a deeper understanding of numerical representation and manipulation. This knowledge is not just confined to the classroom but extends to various practical applications across various disciplines and everyday life. Remember that practice is key; the more you work with fractions and decimals, the more comfortable and proficient you will become in converting between these two important numerical representations.
Latest Posts
Latest Posts
-
How To Find Maximum Revenue
Sep 06, 2025
-
Convert 1 8 To Decimal
Sep 06, 2025
-
Judicial Restraint Strict Constitutionalist Definition Simple
Sep 06, 2025
-
Gcf Of 16 And 48
Sep 06, 2025
-
Is Desmos On The Sat
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about 2 4 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.