3 12 In Decimal Form
zacarellano
Sep 17, 2025 · 5 min read
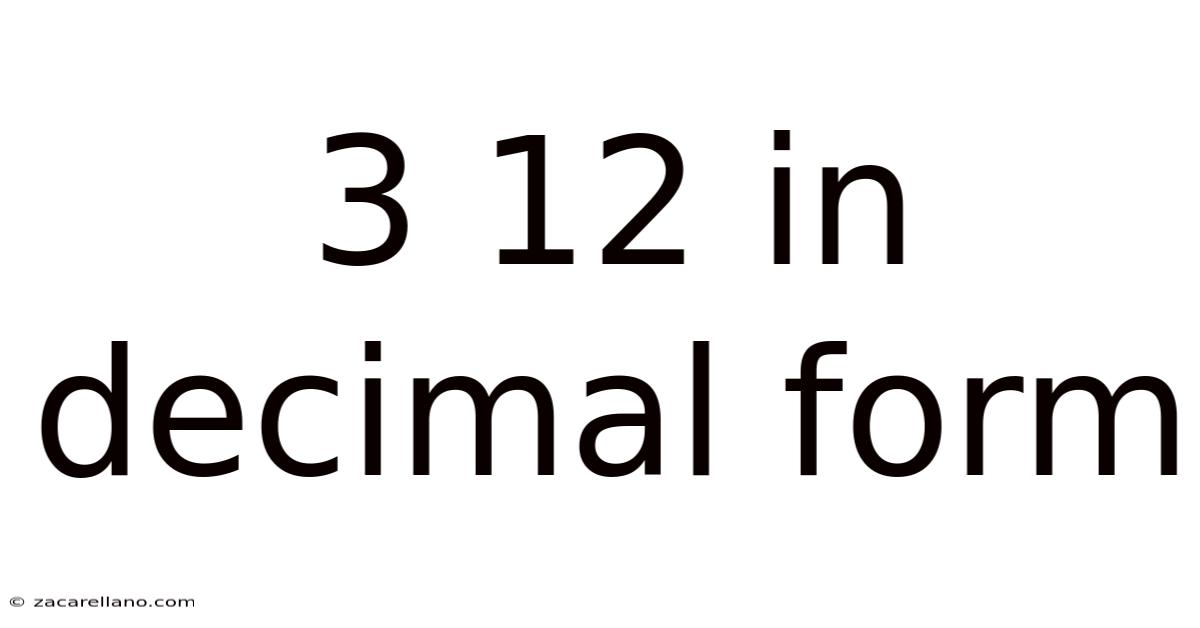
Table of Contents
Decoding 3 12: Understanding Mixed Numbers and Decimal Conversions
The seemingly simple expression "3 12" actually represents a rich mathematical concept involving mixed numbers and their decimal equivalents. This article will delve deep into understanding what 3 12 means, how to convert it into decimal form, and explore the underlying principles involved. We'll cover the conversion process step-by-step, address common misconceptions, and provide examples to solidify your understanding. By the end, you'll not only know the decimal equivalent of 3 12 but also grasp the broader mathematical concepts behind it.
Understanding Mixed Numbers
Before diving into the conversion, let's clarify what "3 12" represents. This is a mixed number, a combination of a whole number (3) and a fraction (12). Mixed numbers are a convenient way to represent values that are greater than one but not whole numbers. The number 3 12 signifies three whole units plus an additional fraction of a unit. However, the notation "3 12" is ambiguous. It needs clarification: is the fraction 1/2, or is it something else like 12/100, 12/1000, or even 12/x where x is another number? We'll consider several interpretations.
Interpretation 1: 3 1/2
The most common interpretation of "3 12" is likely 3 1/2. This means three whole units and one-half of another unit. To convert this mixed number into a decimal, we follow these steps:
Steps to Convert 3 1/2 to Decimal:
-
Convert the fraction to a decimal: Divide the numerator (1) by the denominator (2). 1 ÷ 2 = 0.5
-
Add the whole number: Add the result from step 1 to the whole number (3). 3 + 0.5 = 3.5
Therefore, 3 1/2 in decimal form is 3.5.
Interpretation 2: 3 and 12 Hundredths (3.12)
Another possible interpretation is that "3 12" represents three units and twelve hundredths, written as 3.12. This is a direct decimal representation, needing no conversion from a mixed number. In this case, the decimal value is already given.
Interpretation 3: 3 and 12 Thousandths (3.012)
It's less likely but possible that "3 12" represents three units and twelve thousandths, written as 3 12/1000, This would convert to 3.012. The crucial point here is the placement of the decimal point; a lack of clear fractional notation allows for this ambiguity.
The Importance of Proper Notation
This ambiguity highlights the vital importance of clear and precise mathematical notation. Using a fraction bar (/) or expressing the fraction as a decimal directly avoids any confusion. For example, writing 3 ½, 3 + 1/2, or 3.5 leaves no room for misinterpretation. Likewise, if the intended value was 3.12, writing it as such is far clearer than using the ambiguous form "3 12".
Expanding the Understanding: Decimal Representation and Place Value
The decimal system is based on powers of 10. Each digit in a decimal number holds a specific place value. Consider the number 3.12:
-
3: This digit represents the number of ones (or units).
-
1: This digit represents the number of tenths. It means 1/10.
-
2: This digit represents the number of hundredths. It means 2/100.
Therefore, 3.12 can be expressed as 3 + 1/10 + 2/100. This understanding is fundamental to working with decimals and converting between different numerical representations.
Converting Fractions to Decimals: A Deeper Dive
The process of converting a fraction to a decimal involves division. The numerator is divided by the denominator. For example:
-
1/4: 1 ÷ 4 = 0.25
-
3/8: 3 ÷ 8 = 0.375
-
2/3: 2 ÷ 3 = 0.666... (a repeating decimal)
Some fractions result in terminating decimals (like 1/4 and 3/8), while others produce repeating decimals (like 2/3). Understanding repeating decimals requires exploring concepts like rational and irrational numbers.
Repeating Decimals and Rational Numbers
Repeating decimals are often represented with a bar over the repeating digits. For example, 0.666... is written as 0.6̅. These decimals represent rational numbers, meaning they can be expressed as a fraction of two integers. Irrational numbers, like pi (π), cannot be expressed as a fraction and have non-repeating, non-terminating decimal representations.
Practical Applications of Decimal Conversions
The ability to convert between fractions and decimals is essential in many fields:
-
Engineering: Precise measurements and calculations require accurate decimal representations.
-
Finance: Calculating interest, percentages, and currency conversions heavily relies on decimal arithmetic.
-
Science: Data analysis, experimental measurements, and scientific calculations frequently use decimal numbers.
-
Everyday Life: Many everyday tasks, like calculating tips, discounts, or proportions, involve working with decimal numbers.
Frequently Asked Questions (FAQ)
Q1: What if "3 12" was meant to be a different base?
A1: The ambiguity of "3 12" without any base specification assumes a base-10 system (the decimal system). If it were another base (like base 2, base 16, etc.), the interpretation and conversion would be entirely different.
Q2: How do I convert a decimal back to a fraction?
A2: To convert a decimal to a fraction, consider the place value of the last digit. For example:
* 0.5 is 5/10, which simplifies to 1/2.
* 0.25 is 25/100, which simplifies to 1/4.
* 0.125 is 125/1000, which simplifies to 1/8.
Q3: What are significant figures and how do they relate to decimal precision?
A3: Significant figures indicate the accuracy of a measurement or calculation. When dealing with decimals, significant figures dictate how many digits should be retained after a calculation. For example, a measurement of 3.12 might have three significant figures.
Q4: Can you provide more examples of mixed number to decimal conversions?
A4: Certainly! Here are a few more examples:
* 2 3/4 = 2.75
* 5 1/8 = 5.125
* 1 2/5 = 1.4
Conclusion
The expression "3 12" is inherently ambiguous without proper notation specifying the fractional part. However, by considering its possible interpretations (3 1/2, 3.12, or 3.012), we've explored the core principles of mixed numbers and decimal conversions. Understanding these principles—from place values to the process of division for fractional conversions—is crucial for mastering decimal arithmetic and its extensive applications across diverse fields. Always prioritize clear mathematical notation to avoid ambiguity and ensure accurate communication of numerical values. Remember to use proper notation and always clarify the intended meaning when working with mixed numbers to avoid any confusion.
Latest Posts
Latest Posts
-
Battle Of Yorktown Apush Definition
Sep 17, 2025
-
Velocity At Center Of Mass
Sep 17, 2025
-
Relaciones Interespecificas Parasitismo Caracteristicas Principales
Sep 17, 2025
-
Larger Ka Means Stronger Acid
Sep 17, 2025
-
What Is Heritability In Psychology
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3 12 In Decimal Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.