3 2/5 As A Decimal
zacarellano
Sep 20, 2025 · 6 min read
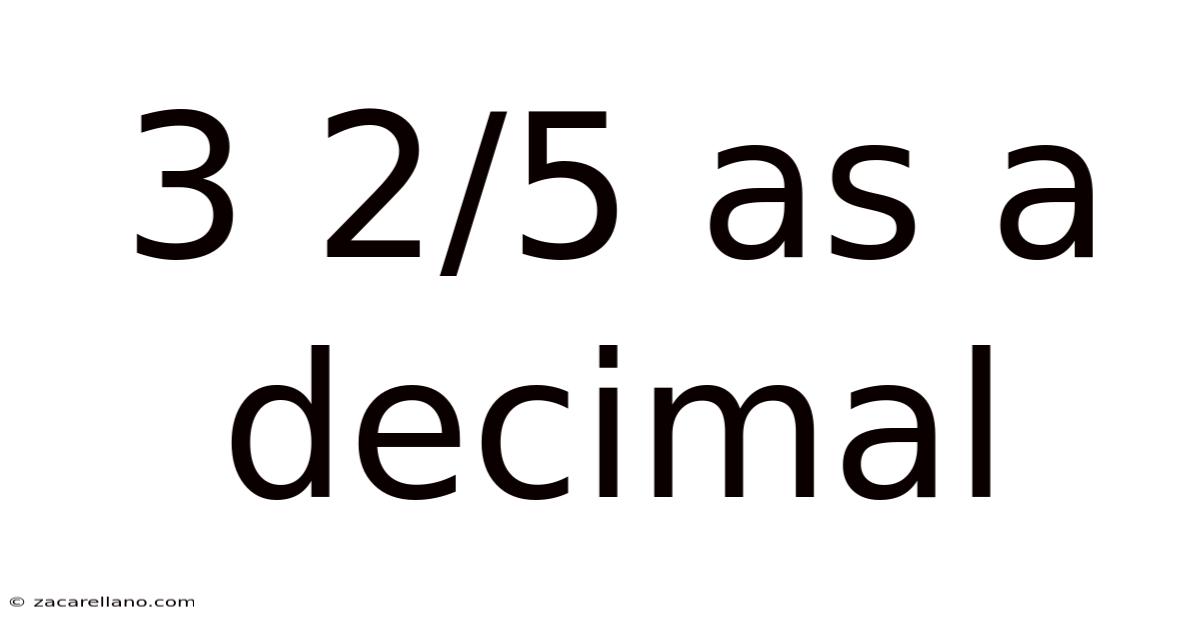
Table of Contents
Converting Fractions to Decimals: A Deep Dive into 3 2/5 as a Decimal
Understanding how to convert fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will explore the process of converting the mixed number 3 2/5 into its decimal equivalent, providing a detailed explanation suitable for learners of all levels. We’ll cover various methods, explore the underlying mathematical principles, and delve into practical applications to solidify your understanding. This will also cover related concepts to help you confidently tackle similar fraction-to-decimal conversions.
Understanding Mixed Numbers and Fractions
Before we jump into the conversion process, let's refresh our understanding of mixed numbers and fractions. A mixed number combines a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). In our case, 3 2/5 is a mixed number: 3 represents the whole number part, and 2/5 is the fractional part. The fraction 2/5 represents two parts out of five equal parts of a whole.
Method 1: Converting the Fraction to a Decimal and Adding the Whole Number
This is arguably the most straightforward approach. We'll first convert the fractional part (2/5) into a decimal, then add the whole number part (3).
-
Convert the fraction to a decimal: To convert a fraction to a decimal, we divide the numerator by the denominator. In this case, we divide 2 by 5:
2 ÷ 5 = 0.4
-
Add the whole number: Now, add the whole number part (3) to the decimal equivalent of the fraction (0.4):
3 + 0.4 = 3.4
Therefore, 3 2/5 as a decimal is 3.4.
Method 2: Converting the Mixed Number to an Improper Fraction, then to a Decimal
This method involves an intermediate step of converting the mixed number into an improper fraction (a fraction where the numerator is greater than or equal to the denominator).
-
Convert to an improper fraction: To convert a mixed number to an improper fraction, we multiply the whole number by the denominator, add the numerator, and keep the same denominator. For 3 2/5:
(3 × 5) + 2 = 17
The improper fraction is 17/5.
-
Convert the improper fraction to a decimal: Now, divide the numerator (17) by the denominator (5):
17 ÷ 5 = 3.4
Again, we arrive at the decimal equivalent of 3.4.
Method 3: Understanding Decimal Place Value
This method offers a deeper understanding of the relationship between fractions and decimals. It emphasizes the concept of decimal place value. The decimal point separates the whole number part from the fractional part. The first digit to the right of the decimal point represents tenths, the second represents hundredths, and so on.
Let's consider 2/5. To express this as a decimal, we need to find an equivalent fraction with a denominator that is a power of 10 (e.g., 10, 100, 1000). In this case, we can multiply both the numerator and denominator by 2:
(2 × 2) / (5 × 2) = 4/10
This fraction, 4/10, is equivalent to 0.4, since 4 represents 4 tenths. Adding the whole number 3, we get 3.4.
The Significance of Understanding Decimal Conversions
Converting fractions to decimals is a vital skill in numerous contexts:
- Everyday calculations: Many everyday tasks, such as calculating discounts, splitting bills, or measuring ingredients, involve working with both fractions and decimals.
- Scientific computations: Scientific fields like physics, chemistry, and engineering rely heavily on accurate decimal representations for calculations and data analysis.
- Financial applications: In finance, understanding decimal equivalents is essential for accurate calculations of interest rates, stock prices, and other financial metrics.
- Computer programming: Many programming languages use decimal representation for numerical data, requiring programmers to understand how to convert between different numerical formats.
- Data analysis and statistics: Decimal representation is crucial in data analysis for accurate calculations and interpretations of statistical measures.
Expanding on the Concept: Converting Other Fractions to Decimals
The methods outlined above can be applied to convert other fractions to decimals. Here are some examples:
- 1/4: 1 ÷ 4 = 0.25
- 3/8: 3 ÷ 8 = 0.375
- 5/2: 5 ÷ 2 = 2.5 (Note: this results in a whole number and a decimal)
- 7/100: 7 ÷ 100 = 0.07
For fractions with denominators that are not easily converted to powers of 10, long division is usually necessary. However, the basic principle remains the same: divide the numerator by the denominator.
Dealing with Repeating Decimals
Some fractions, when converted to decimals, result in repeating decimals (decimals with a digit or sequence of digits that repeat infinitely). For instance, 1/3 = 0.333... (the 3 repeats infinitely). These repeating decimals are often represented using a bar over the repeating digit(s), such as 0.3̅. Understanding how to represent and work with repeating decimals is another important aspect of this mathematical skill.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to convert 3 2/5 to a decimal?
A: The easiest method is to first convert the fraction 2/5 to a decimal (0.4) by dividing the numerator (2) by the denominator (5), and then add the whole number (3), resulting in 3.4.
Q: Why is it important to understand fraction-to-decimal conversions?
A: This skill is fundamental in various aspects of life, from everyday calculations to advanced scientific and financial applications. It's crucial for seamless transitions between different numerical formats.
Q: Can all fractions be converted to terminating decimals (decimals that end)?
A: No, some fractions result in repeating decimals. This often happens when the denominator of the fraction, in its simplest form, contains prime factors other than 2 or 5.
Q: How do I handle fractions with larger numbers?
A: The same principles apply. Use long division to divide the numerator by the denominator. You might need a calculator for larger numbers to ensure accuracy.
Q: What if the fraction is negative?
A: If the fraction is negative (e.g., -3 2/5), simply convert the fraction to a decimal as described above and then add a negative sign to the result (-3.4).
Conclusion
Converting fractions to decimals is a crucial skill with wide-ranging applications. Through understanding the various methods, from direct division to converting to improper fractions, and grasping the underlying principles of place value, you can confidently tackle fraction-to-decimal conversions of various complexities. Remember the key steps: divide the numerator by the denominator, and add the whole number if dealing with a mixed number. Mastering this skill will significantly enhance your mathematical abilities and problem-solving skills across diverse domains. Practice regularly with different types of fractions to solidify your understanding and improve your efficiency.
Latest Posts
Latest Posts
-
Elem Draw Is Not A Function
Sep 20, 2025
-
Word Problems On Geometric Sequence
Sep 20, 2025
-
Momentum And Center Of Mass
Sep 20, 2025
-
Are Complex Numbers Real Numbers
Sep 20, 2025
-
Energy Required For Active Transport
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 3 2/5 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.