3/6 On A Number Line
zacarellano
Sep 14, 2025 · 6 min read
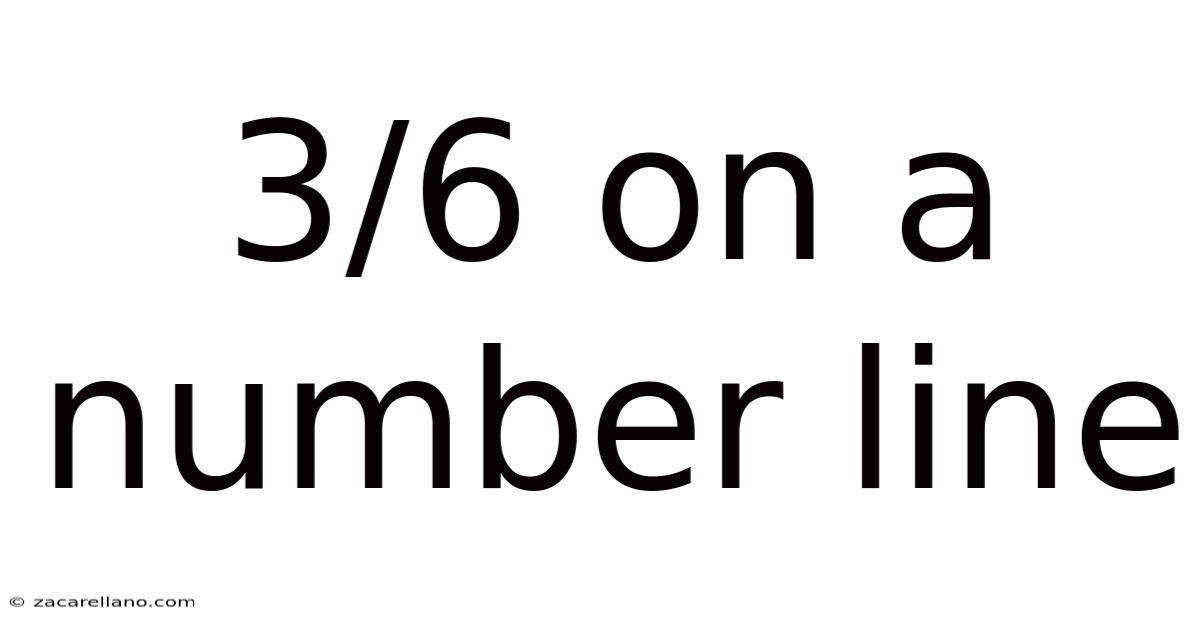
Table of Contents
Understanding 3/6 on the Number Line: A Comprehensive Guide
Understanding fractions can be a challenge, but visualizing them on a number line can make the process much clearer. This article will delve deep into the concept of representing 3/6 on a number line, exploring its meaning, equivalent fractions, and its place within the broader context of fractions and decimals. We'll also address frequently asked questions to solidify your understanding. This comprehensive guide is designed for students, parents, and educators alike, offering a practical and engaging approach to mastering this fundamental mathematical concept.
Introduction: What is a Fraction?
Before we pinpoint 3/6 on a number line, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written as a/b, where 'a' is the numerator (the number of parts we have) and 'b' is the denominator (the total number of equal parts the whole is divided into). For example, in the fraction 3/6, 3 is the numerator and 6 is the denominator. This means we're considering 3 parts out of a total of 6 equal parts.
The number line is a visual representation of numbers, extending infinitely in both positive and negative directions. It's a powerful tool for understanding the relative positions and magnitudes of numbers, including fractions.
Locating 3/6 on the Number Line: A Step-by-Step Approach
To accurately place 3/6 on the number line, we need to follow a methodical approach:
1. Define the Whole: First, we need to define the length of our number line representing the "whole." This could be any length you choose, but for simplicity, let's use a line from 0 to 1.
2. Divide the Whole: The denominator of our fraction, 6, tells us to divide the whole (the line from 0 to 1) into 6 equal parts. This involves creating five equally spaced markers between 0 and 1.
3. Identify the Numerator: The numerator of our fraction, 3, indicates the number of parts we need to count from 0.
4. Locate 3/6: Starting at 0, count three of the six equal parts. The point you land on represents the fraction 3/6.
Visual Representation: The Number Line with 3/6
Imagine a number line:
0----|----|----|----|----|----|1
1/6 2/6 3/6 4/6 5/6 6/6
The point marked "3/6" is precisely one-half of the distance between 0 and 1.
Equivalent Fractions: Simplifying 3/6
An important concept to grasp is that fractions can have equivalent representations. This means different fractions can represent the same value. 3/6 is an example of a fraction that can be simplified.
To simplify a fraction, we find the greatest common divisor (GCD) of the numerator and the denominator and divide both by it. The GCD of 3 and 6 is 3.
Dividing both the numerator (3) and the denominator (6) by 3, we get:
3 ÷ 3 / 6 ÷ 3 = 1/2
Therefore, 3/6 is equivalent to 1/2. This means that on the number line, 3/6 and 1/2 occupy the exact same position.
3/6, 1/2, and Decimal Equivalents: A Unified Perspective
The equivalence between 3/6 and 1/2 extends to their decimal representations. To convert a fraction to a decimal, we divide the numerator by the denominator:
1 ÷ 2 = 0.5
Thus, 3/6, 1/2, and 0.5 all represent the same value and would all be plotted at the same point on the number line, halfway between 0 and 1.
Understanding Fractions Greater Than One
While our example focuses on 3/6, which is less than one (a proper fraction), it's crucial to understand how to represent improper fractions (fractions where the numerator is greater than the denominator) and mixed numbers (a whole number and a fraction) on the number line.
For instance, consider the fraction 7/6. This is an improper fraction. To represent it on the number line, we first recognize that 7/6 is equivalent to 1 and 1/6. We would plot this point at a distance of 1 and 1/6 from 0. The number line would extend beyond 1 to accommodate this value.
Similarly, mixed numbers like 2 1/3 are easily represented. We first identify the whole number part (2), and then add the fractional part (1/3) to that position on the number line.
Connecting Fractions to Real-World Examples
Understanding fractions isn't just about abstract mathematical concepts; they are vital for everyday life. Here are a few examples:
-
Sharing: If you have 6 cookies and want to share them equally among 3 friends, each friend gets 2 cookies (6/3 = 2). This is the inverse of the fraction we discussed, but showcases the practical application.
-
Measurement: Imagine a recipe that calls for 3/6 of a cup of sugar. This is equivalent to 1/2 a cup, a much easier measurement to manage.
-
Time: Thinking about time in terms of fractions is also useful. 3/6 of an hour is equivalent to 30 minutes (1/2 an hour).
Frequently Asked Questions (FAQ)
Q: Why is it important to simplify fractions?
A: Simplifying fractions makes them easier to understand and work with. It presents the fraction in its most concise form, revealing its true value more clearly. It’s also essential for accurate calculations and comparisons.
Q: Can I use a different scale on the number line?
A: Absolutely! The scale of the number line is flexible. You can use a line from 0 to 2, 0 to 10, or any other range, as long as you divide it into the correct number of equal parts according to the denominator of the fraction.
Q: What if the denominator is a large number?
A: If the denominator is a large number, the divisions on the number line will be smaller and more numerous. While it might be more challenging to draw precisely, the principle remains the same: divide the chosen length into the specified number of equal parts.
Q: How do I represent negative fractions on a number line?
A: Negative fractions are represented on the left side of 0 on the number line. For example, -3/6 would be located to the left of 0, at the same distance as 3/6 is to the right of 0.
Q: Is it always necessary to draw a number line?
A: While drawing a number line is a valuable visual aid, especially for beginners, it isn’t always strictly necessary. With practice, you’ll develop an intuitive sense of where fractions lie on the number line without needing a physical representation.
Conclusion: Mastering Fractions Through Visualization
Understanding the position of 3/6 on a number line is a stepping stone to mastering fractions. By visualizing fractions on a number line, we gain a deeper understanding of their magnitude, relationships, and equivalence. This approach not only simplifies the learning process but also strengthens the foundation for more advanced mathematical concepts. Remember the importance of simplifying fractions, recognizing equivalent values, and applying these concepts to real-world scenarios. Through practice and visualization, mastering fractions becomes an achievable and even enjoyable experience. The ability to represent and understand fractions confidently lays the groundwork for success in more complex mathematical endeavors.
Latest Posts
Latest Posts
-
Two Step Equations With Decimals
Sep 14, 2025
-
5 3 With An Attitude
Sep 14, 2025
-
Clear And Present Danger Rule
Sep 14, 2025
-
Gcf Of 24 And 9
Sep 14, 2025
-
Art Based Question Pns Question 1
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 3/6 On A Number Line . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.