4 5 X 5 8
zacarellano
Sep 09, 2025 · 6 min read
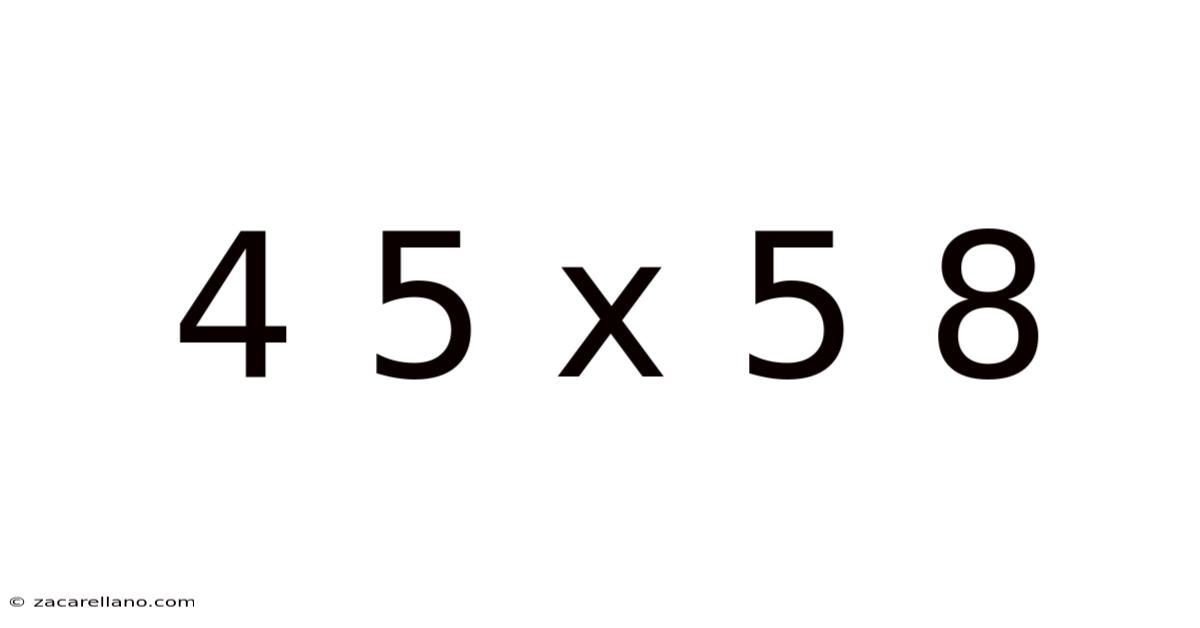
Table of Contents
Decoding 4 x 5 x 5 x 8: Exploring Multiplication, Volume, and Beyond
This article delves into the seemingly simple mathematical expression "4 x 5 x 5 x 8," exploring its various interpretations, applications, and the underlying mathematical principles. We will move beyond the basic calculation to uncover its relevance in geometry, real-world problem-solving, and even its connection to more advanced mathematical concepts. This exploration is designed to be accessible to a wide range of readers, from those revisiting basic arithmetic to those seeking a deeper understanding of mathematical applications.
Understanding the Fundamentals: Basic Multiplication
At its core, "4 x 5 x 5 x 8" represents a series of multiplications. It's a straightforward calculation that can be approached in several ways. The order of operations doesn't affect the final result due to the commutative property of multiplication. We can solve this using several methods:
-
Step-by-step multiplication: We can perform the operations sequentially: 4 x 5 = 20; 20 x 5 = 100; 100 x 8 = 800.
-
Grouping: We can group the numbers strategically to simplify the calculation: (4 x 8) x (5 x 5) = 32 x 25 = 800. This method leverages the associative property of multiplication.
-
Using a calculator: For larger or more complex calculations, a calculator provides a quick and accurate solution.
The answer, regardless of the approach, is 800. This seemingly simple calculation forms the basis for understanding more complex mathematical concepts and real-world applications.
Geometry and Volume: A Practical Application
One of the most immediate and practical applications of "4 x 5 x 5 x 8" lies in the realm of geometry, specifically in calculating volume. Imagine a rectangular prism (a box-shaped object) with the following dimensions:
- Length: 4 units
- Width: 5 units
- Height: 5 x 8 = 40 units (this could represent a stacked configuration)
The volume of a rectangular prism is calculated by multiplying its length, width, and height. Therefore, the volume of this prism would be:
4 x 5 x 40 = 800 cubic units.
This illustrates how the multiplication problem directly translates to a real-world scenario. Consider different units of measurement:
- Cubic centimeters (cm³): This might represent a small box.
- Cubic meters (m³): This might represent a larger storage container.
- Cubic feet (ft³): This might represent the volume of a room.
The principle remains the same; the calculation provides the volume of the three-dimensional space encompassed by the prism. This has numerous applications in various fields, including:
- Engineering: Calculating material requirements for construction projects.
- Packaging: Determining the size and capacity of shipping containers.
- Architecture: Estimating the space within a building.
Beyond the Basics: Exploring Related Concepts
The simple calculation of 4 x 5 x 5 x 8 opens doors to a broader understanding of several related mathematical concepts:
Factors and Multiples:
- Factors: The numbers 4, 5, and 8 are factors of 800. A factor is a number that divides another number without leaving a remainder.
- Multiples: 800 is a multiple of 4, 5, and 8. A multiple is a number obtained by multiplying a given number by an integer.
- Prime Factorization: We can break down 800 into its prime factors: 2<sup>5</sup> x 5<sup>2</sup>. This is a fundamental concept in number theory.
Exponents and Powers:
The expression could be rewritten using exponents: 4 x 5<sup>2</sup> x 8 = 800. This shows the power of 5 (5 multiplied by itself) within the calculation. Understanding exponents is crucial for advanced mathematics and various scientific applications.
Order of Operations (PEMDAS/BODMAS):
While the order of operations doesn't change the result in this specific case (because it only involves multiplication), understanding PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) is vital for solving more complex mathematical expressions involving different operations.
Real-World Applications Beyond Geometry
The multiplication 4 x 5 x 5 x 8 has applications beyond simple volume calculations. Consider these examples:
-
Inventory Management: A warehouse might have 4 rows of shelves, each with 5 shelves, each containing 5 boxes, each holding 8 items. The total number of items would be 800.
-
Event Planning: Imagine planning a large event with 4 sections, each needing 5 tables, each seating 5 people, with each person needing 8 items (e.g., napkins, utensils). The total number of items needed would be 800.
-
Data Analysis: Imagine a dataset with 4 categories, 5 subcategories within each category, 5 data points in each subcategory, and 8 measurements per data point. The total number of measurements would be 800.
Expanding the Problem: Variations and Extensions
Let's consider variations of the problem to further enhance understanding:
-
Changing the Numbers: What if we changed the numbers? How would the result change if we replaced 4 with 6, 5 with 3, and 8 with 10? This exercise helps in understanding the impact of each number on the final outcome.
-
Adding More Dimensions: What if we added another dimension? This would involve moving beyond the calculation of a simple rectangular prism's volume into more complex geometric shapes.
-
Introducing Different Operations: Incorporating addition, subtraction, or division alongside multiplication would increase the complexity of the problem and require a deeper understanding of the order of operations.
Frequently Asked Questions (FAQ)
Q: Is there only one way to solve 4 x 5 x 5 x 8?
A: No, there are multiple ways to approach the calculation, as demonstrated earlier using different groupings and step-by-step methods. The order of operations doesn't affect the final answer in this case.
Q: What are some real-world examples where this type of calculation is used?
A: Numerous examples exist, ranging from simple volume calculations to more complex scenarios involving inventory, event planning, and data analysis, as discussed in the article.
Q: How does this calculation relate to more advanced mathematical concepts?
A: The simple calculation forms the basis for understanding factors, multiples, prime factorization, exponents, and the order of operations—all crucial concepts for advanced mathematics.
Q: Can this calculation be used in other areas of study besides mathematics?
A: Absolutely! The underlying principles of multiplication and volume calculation are applicable in various fields, including engineering, architecture, physics, and computer science.
Conclusion
The seemingly simple mathematical expression "4 x 5 x 5 x 8" serves as a gateway to a deeper understanding of fundamental mathematical principles and their real-world applications. From basic multiplication to the calculation of volume and beyond, this expression highlights the interconnectedness of mathematical concepts and their importance in various fields. By exploring its different facets, we've not only solved the problem but also uncovered its significance in a broader context, emphasizing the practical value of even seemingly basic mathematical operations. The ability to break down complex problems into smaller, manageable parts is a skill transferable far beyond the realm of mathematics, applicable to problem-solving in all aspects of life.
Latest Posts
Latest Posts
-
Whos The Founder Of Christianity
Sep 10, 2025
-
Gcf Of 40 And 48
Sep 10, 2025
-
E1 And E2 Practice Problems
Sep 10, 2025
-
Stat3 Y705 Mitochondria Oxidative Phosphorylation
Sep 10, 2025
-
3 Models Of Dna Replication
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 4 5 X 5 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.