4 X 3 X 10
zacarellano
Sep 17, 2025 · 7 min read
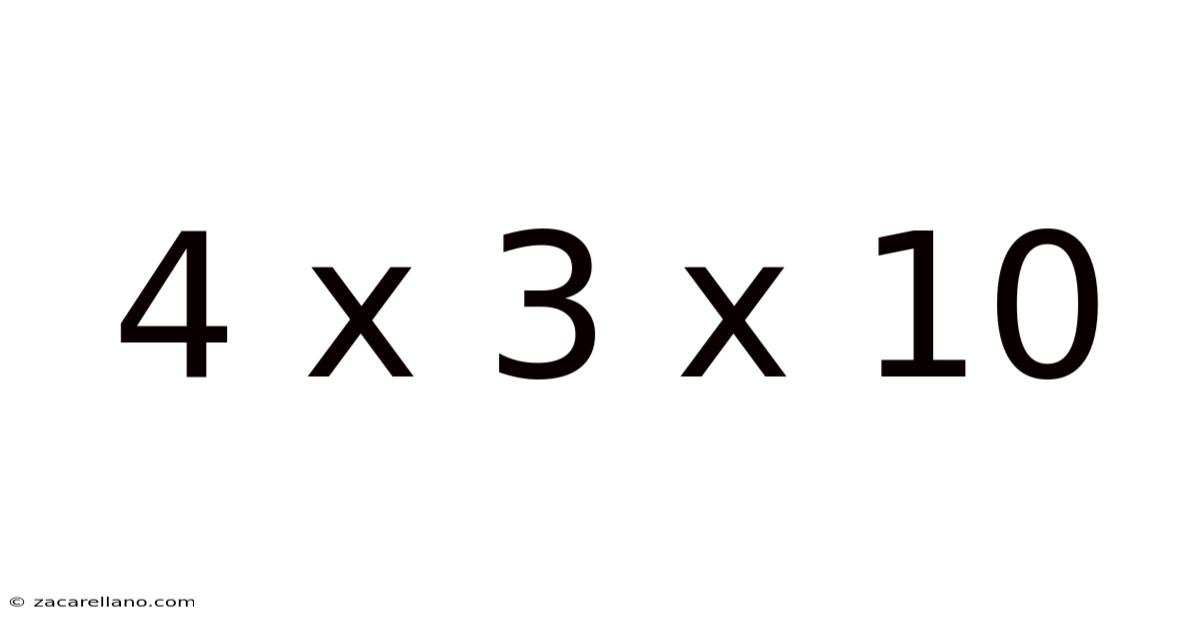
Table of Contents
Decoding 4 x 3 x 10: Exploring Multiplication, Volume, and Real-World Applications
This article delves into the seemingly simple mathematical expression "4 x 3 x 10," exploring its fundamental meaning in multiplication, its application in calculating volume, and its relevance in various real-world scenarios. We'll unpack the calculation itself, discuss different approaches to solving it, and then move beyond the basic arithmetic to understand its practical implications. This exploration will be accessible to all levels, from elementary school students grasping multiplication to those seeking a deeper understanding of its applications. This comprehensive guide aims to illuminate the multifaceted nature of this seemingly simple equation and its significance in our daily lives.
Understanding the Basics: Multiplication
At its core, "4 x 3 x 10" represents a multiplication problem. Multiplication is a fundamental arithmetic operation that essentially involves repeated addition. In this case, we're multiplying four by three, and then multiplying the result by ten. Each number represents a distinct quantity or dimension.
-
4: This could represent four units of something. Think of it as four boxes, four apples, or four anything.
-
3: Similarly, this represents three units. It could be three rows, three layers, or three of any other item.
-
10: This represents ten units, potentially ten stacks, ten columns, or ten of whatever unit is being considered.
The "x" symbol signifies multiplication. We could also represent this equation using parentheses, such as (4 x 3) x 10 or 4 x (3 x 10). The associative property of multiplication dictates that the order in which we perform these operations doesn’t change the final result.
Let's break down the calculation step-by-step:
-
4 x 3 = 12: Four multiplied by three equals twelve. Imagine arranging four rows of three apples; you would have a total of twelve apples.
-
12 x 10 = 120: Twelve multiplied by ten equals one hundred and twenty. Continuing our apple example, if you had ten such groups of twelve apples, you'd have 120 apples in total.
Therefore, 4 x 3 x 10 = 120. This is the fundamental answer, but the true understanding lies in grasping its applications beyond this simple numerical result.
Volume Calculation: A Key Application
One of the most common practical applications of "4 x 3 x 10" is in calculating the volume of a rectangular prism (also known as a cuboid). Imagine a box with these dimensions:
- Length: 4 units (e.g., 4 meters, 4 centimeters, 4 inches)
- Width: 3 units (using the same unit of measurement as the length)
- Height: 10 units (again, using the same unit of measurement)
The volume of this box is calculated by multiplying its length, width, and height: Volume = Length x Width x Height = 4 x 3 x 10 = 120 cubic units. The "cubic" signifies that the volume is measured in three dimensions. If our units were centimeters, the volume would be 120 cubic centimeters (cm³). Similarly, if the units were meters, it would be 120 cubic meters (m³).
Real-World Examples: From Packaging to Construction
The calculation of volume using "4 x 3 x 10" has numerous real-world applications across various fields:
-
Packaging and Shipping: Companies use this calculation to determine the volume of boxes needed to ship products, ensuring efficient packing and minimizing wasted space. The dimensions of the product and its packaging directly inform the calculation, affecting shipping costs and overall logistics.
-
Construction and Engineering: Architects and engineers utilize this principle when calculating the volume of materials required for construction projects. This is crucial in determining the amount of concrete, bricks, or other building materials needed for a particular structure. Accurate volume calculations are essential for effective project management and cost estimation.
-
Agriculture and Storage: Farmers use volume calculations to determine the capacity of silos for storing grain or other agricultural products. Understanding the volume helps in planning storage space and ensuring efficient utilization of resources.
-
Aquariums and Pools: The volume of an aquarium or swimming pool is essential for calculating the amount of water needed to fill it. This calculation impacts the cost of water and the necessary filtration systems.
-
Manufacturing and Production: Industrial processes often involve calculating the volume of materials used in manufacturing. Understanding the dimensions of products and materials is critical for optimizing production lines and managing inventory.
Beyond the Numbers: Expanding the Concept
The equation 4 x 3 x 10 transcends mere numerical computation; it represents a fundamental understanding of spatial relationships and dimensional analysis. It introduces the concept of scaling and proportionality. If we were to double the length of the box, for example, the volume would also double (8 x 3 x 10 = 240). This illustrates how changes in one dimension directly affect the overall volume.
Furthermore, this equation can be used as a basis for exploring more complex geometrical concepts. For instance, it forms the foundation for understanding the volumes of more intricate shapes, which are often broken down into simpler rectangular prisms for calculation. This decomposition approach is frequently employed in calculus and other advanced mathematical fields.
Exploring Different Approaches: Visualizations and Manipulations
While the standard calculation (4 x 3 x 10) provides a straightforward answer, exploring alternative approaches can enhance comprehension:
-
Visual Representation: Creating a physical model of a 4 x 3 x 10 rectangular prism using blocks or drawing a 3D diagram helps visualize the dimensions and the overall volume. This visual approach strengthens the connection between the abstract numerical equation and its physical representation.
-
Rearranging the Factors: The commutative and associative properties of multiplication allow us to rearrange the factors without changing the outcome. We could calculate (4 x 10) x 3 or (3 x 10) x 4, arriving at the same answer (120). This demonstrates the flexibility inherent in the calculation.
-
Using Mental Math Techniques: Practicing mental math techniques can improve calculation speed and accuracy. For example, it’s easier to calculate 4 x 3 as 12, and then multiply by 10 (adding a zero) to obtain 120.
Frequently Asked Questions (FAQ)
Q: What if the numbers were different? How would the calculation change?
A: The calculation process remains the same, regardless of the numbers. Simply substitute the new values for length, width, and height, and perform the multiplication. The result will represent the volume of the new rectangular prism.
Q: Can this equation be applied to shapes other than rectangular prisms?
A: Directly, no. This equation is specifically designed for calculating the volume of rectangular prisms. However, the principle of multiplying dimensions is fundamental to calculating the volume of other shapes, albeit with more complex formulas.
Q: What are the units of measurement typically used for volume?
A: Common units include cubic meters (m³), cubic centimeters (cm³), cubic feet (ft³), and cubic inches (in³). The choice of unit depends on the scale of the object being measured.
Q: Why is understanding volume important?
A: Understanding volume is crucial for numerous practical reasons, from efficient packaging and construction to accurate material estimations and resource management in various fields. It's a fundamental concept in physics, engineering, and numerous other disciplines.
Conclusion: The Power of a Simple Equation
The seemingly simple equation "4 x 3 x 10" encapsulates a wealth of mathematical concepts and real-world applications. While its solution (120) is straightforward, understanding the underlying principles of multiplication, volume calculation, and dimensional analysis is crucial. By grasping these concepts, we can apply this simple equation to numerous practical scenarios, improving efficiency, accuracy, and problem-solving skills in diverse fields. The true power of this equation lies not merely in its numerical result but in its ability to illuminate the interconnectedness of mathematics and the physical world around us. This exploration has hopefully moved beyond the simple arithmetic to reveal the depth and breadth of its practical significance.
Latest Posts
Latest Posts
-
Changes In Nominal Gdp Reflect
Sep 17, 2025
-
Graph Parallel And Perpendicular Lines
Sep 17, 2025
-
Federal Funds Rate Ap Macro
Sep 17, 2025
-
How To Identify Redox Reaction
Sep 17, 2025
-
Reactants Of Light Independent Reaction
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 4 X 3 X 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.