5 More Than -2 Is
zacarellano
Sep 10, 2025 · 6 min read
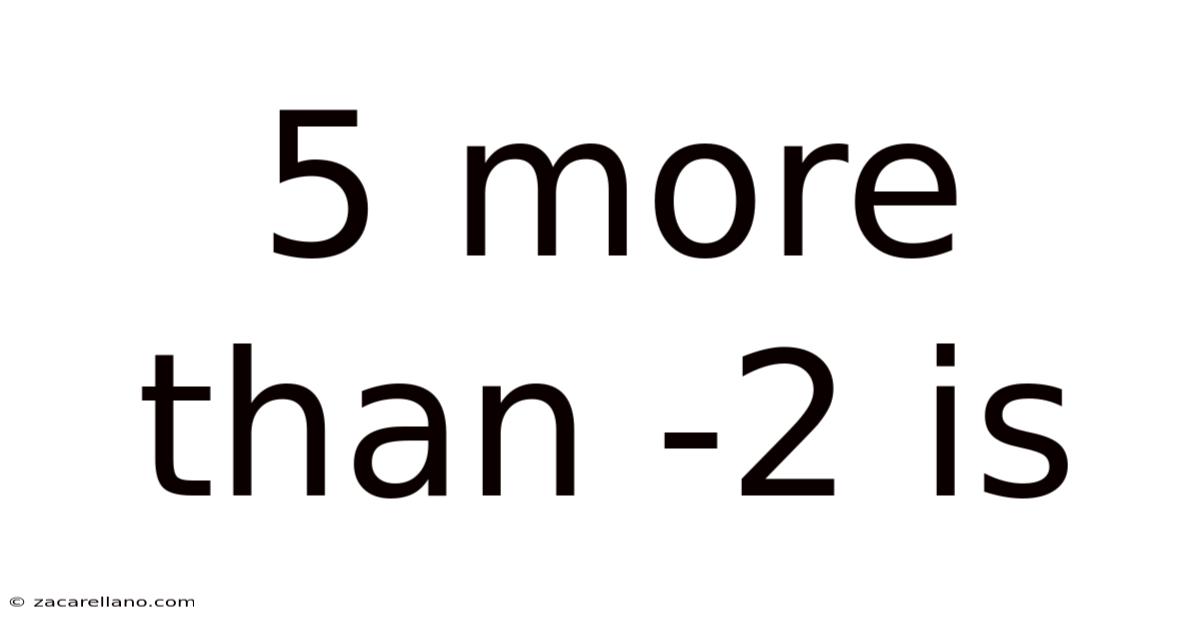
Table of Contents
5 More Than -2 Is: Unpacking the Concept of Integer Addition
This article explores the seemingly simple yet fundamentally important mathematical concept: "5 more than -2 is?". We'll delve into the world of integers, specifically focusing on addition involving negative numbers, providing a clear and comprehensive understanding suitable for learners of all levels. This explanation will cover not just the answer but the underlying principles and practical applications, ensuring a strong grasp of this crucial arithmetic skill. Understanding integer addition is a cornerstone for more advanced mathematical concepts.
Introduction: Understanding Integers and the Number Line
Before we tackle the problem, let's refresh our understanding of integers. Integers are whole numbers, including zero, and their negative counterparts. This means the set of integers includes ..., -3, -2, -1, 0, 1, 2, 3, ... The number line is a visual representation of integers, with zero at the center, positive numbers extending to the right, and negative numbers extending to the left.
Visualizing integers on a number line is incredibly helpful when performing addition and subtraction. Each number's position relative to zero indicates its value. Moving to the right represents addition, while moving to the left represents subtraction.
Solving "5 More Than -2 Is": A Step-by-Step Approach
The phrase "5 more than -2" translates directly into a mathematical expression: -2 + 5. We can solve this using several methods:
1. The Number Line Method:
Start at -2 on the number line. Since we're adding 5, we move 5 units to the right (because we're adding a positive number). Counting five steps to the right from -2 brings us to 3.
Therefore, 5 more than -2 is 3.
2. The Additive Inverse Method:
This method uses the concept of additive inverses. The additive inverse of a number is the number that, when added to the original number, results in zero. For example, the additive inverse of -2 is 2, and the additive inverse of 5 is -5.
We can rewrite -2 + 5 as 5 + (-2). Now, consider the number line again. Starting at 0, we move 5 units to the right (positive 5). Then, we move 2 units to the left (because it's -2). This leaves us at 3.
Thus, -2 + 5 = 3.
3. The Rules of Integer Addition:
When adding integers, consider the following rules:
- Adding two positive integers: Add the numbers together. The result is positive.
- Adding two negative integers: Add the absolute values of the numbers together. The result is negative.
- Adding a positive and a negative integer: Subtract the smaller absolute value from the larger absolute value. The result takes the sign of the number with the larger absolute value.
In our case (-2 + 5), we have a negative and a positive integer. The absolute value of -2 is 2, and the absolute value of 5 is 5. Subtracting the smaller absolute value (2) from the larger absolute value (5) gives us 3. Since 5 (the positive number) has a larger absolute value, the result is positive 3.
Further Exploration: Real-World Applications and Extensions
Understanding integer addition is crucial for numerous real-world scenarios:
- Finance: Tracking income and expenses. A negative number represents debt or expenses, while a positive number represents income or assets. Adding these integers helps determine net worth. For example, if you have -$20 in your account (debt) and receive $25 (income), you end up with $5.
- Temperature: Calculating temperature changes. A temperature drop is represented by a negative number, and a temperature rise is represented by a positive number. For example, if the temperature is -2°C and it rises by 5°C, the new temperature is 3°C.
- Elevation: Measuring changes in altitude. Negative numbers represent elevations below sea level, and positive numbers represent elevations above sea level.
- Game Scoring: In games involving both positive and negative points, tracking the score requires understanding integer addition.
Beyond the simple example of "5 more than -2," let's extend our understanding to more complex scenarios:
Adding More Than Two Integers:
Consider the expression -2 + 5 + (-3) + 7. We can solve this by adding the numbers sequentially:
- -2 + 5 = 3
- 3 + (-3) = 0
- 0 + 7 = 7
Therefore, -2 + 5 + (-3) + 7 = 7. Alternatively, you can group positive and negative integers separately and then add the results: (5 + 7) + (-2 + -3) = 12 + (-5) = 7.
Subtraction as Addition:
Subtraction of integers can be viewed as the addition of the additive inverse. For example, -2 - 5 is the same as -2 + (-5). Using the rules of integer addition, -2 + (-5) = -7.
Properties of Integer Addition:
Integer addition follows several important properties:
- Commutative Property: The order of addition doesn't change the result. a + b = b + a. For example, 5 + (-2) = (-2) + 5 = 3.
- Associative Property: The grouping of numbers during addition doesn't change the result. (a + b) + c = a + (b + c). For example, (5 + (-2)) + 3 = 5 + ((-2) + 3) = 6.
- Identity Property: Adding zero to any integer doesn't change its value. a + 0 = a.
Addressing Common Misconceptions
A common misconception is that adding a positive number to a negative number always results in a positive number. This is incorrect. The sign of the result depends on the magnitudes of the positive and negative numbers. If the absolute value of the negative number is greater than the positive number, the result will be negative.
Another misconception is treating negative numbers as "smaller" than positive numbers in all contexts. While -5 is less than 5 on the number line, their magnitudes (distances from zero) differ. The magnitude of -5 is 5, while the magnitude of 5 is 5.
Frequently Asked Questions (FAQ)
Q: What is the difference between "5 more than -2" and "5 less than -2"?
A: "5 more than -2" means adding 5 to -2, resulting in 3. "5 less than -2" means subtracting 5 from -2, resulting in -7.
Q: Can I use a calculator to solve integer addition problems?
A: Yes, most calculators can handle integer addition. Ensure you understand how to input negative numbers correctly (often using a +/- key or a separate negative sign key).
Q: Why is understanding integer addition important?
A: Integer addition is a fundamental concept in mathematics. It forms the basis for more advanced topics such as algebra, calculus, and various scientific and engineering applications.
Q: Are there different ways to represent "5 more than -2"?
A: Yes, it can also be expressed as:
- -2 + 5
- 5 + (-2)
- The sum of -2 and 5
- Increasing -2 by 5
Conclusion: Mastering Integer Addition
Mastering integer addition is a crucial skill that builds a strong foundation for future mathematical endeavors. By understanding the number line, applying the rules of integer addition, and practicing various problem-solving approaches, you can confidently tackle more complex mathematical concepts. Remember to visualize the process on the number line and to consider the absolute values and signs of the integers involved. Practice consistently, and you will develop fluency in solving these types of problems. The seemingly simple question, "5 more than -2 is?", opens the door to a much deeper understanding of the fascinating world of numbers.
Latest Posts
Latest Posts
-
What Makes An Equation True
Sep 10, 2025
-
Identify Parts Of A Wave
Sep 10, 2025
-
Who Brought Christianity To America
Sep 10, 2025
-
Negative 5 Minus Negative 2
Sep 10, 2025
-
Lcm Of 24 And 32
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 5 More Than -2 Is . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.