5 X 6 X 4
zacarellano
Sep 16, 2025 · 6 min read
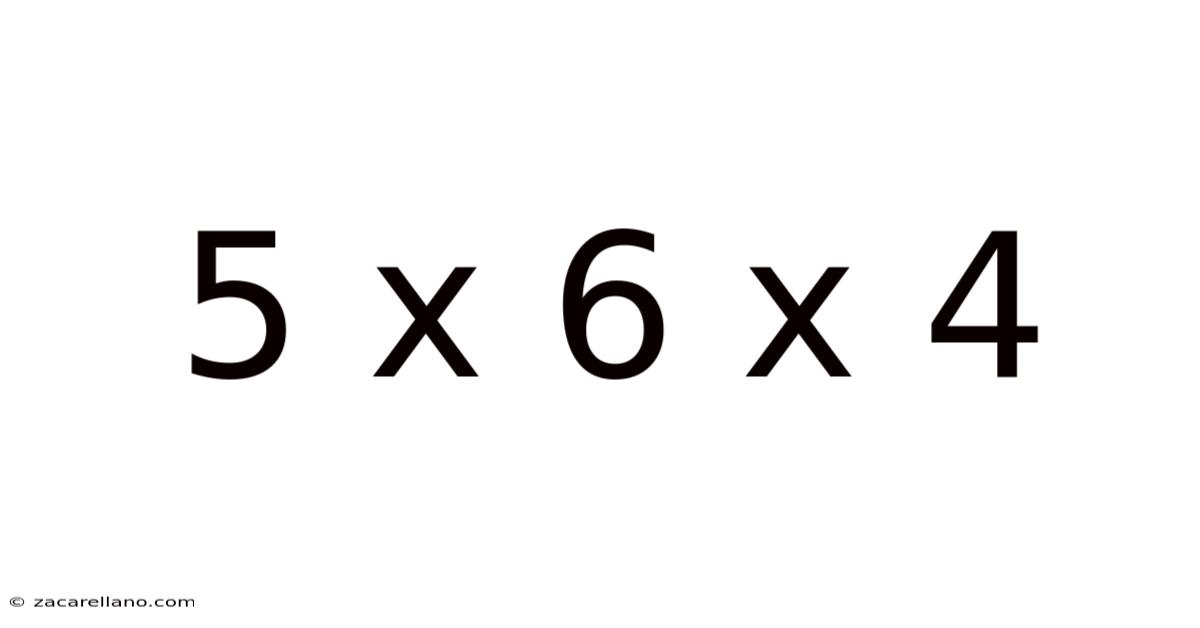
Table of Contents
Decoding 5 x 6 x 4: A Deep Dive into Volume, Multiplication, and Real-World Applications
This article explores the seemingly simple mathematical expression "5 x 6 x 4," delving far beyond the basic calculation. We'll uncover its significance in understanding volume, explore various multiplication strategies, examine its real-world applications, and address common misconceptions surrounding multiplication. Understanding this seemingly simple equation opens doors to a broader comprehension of mathematical concepts and their practical relevance.
Understanding the Basics: Multiplication and Volume
At its core, "5 x 6 x 4" represents a multiplication problem. Multiplication is a fundamental arithmetic operation that signifies repeated addition. In this case, we're repeatedly adding the number 5, six times, and then multiplying the result by four. The solution, 120, represents the product of these three numbers.
But the significance of "5 x 6 x 4" goes beyond simple multiplication. It elegantly represents the calculation of volume. Volume is the amount of three-dimensional space occupied by an object or substance. When we multiply three dimensions (length, width, and height), we obtain the volume. Think of a rectangular prism (or box):
- 5 could represent the length.
- 6 could represent the width.
- 4 could represent the height.
Therefore, 5 x 6 x 4 = 120 represents the volume of this rectangular prism, typically measured in cubic units (e.g., cubic centimeters, cubic meters, cubic inches). This seemingly simple equation forms the foundation for calculating volumes of various shapes, leading to applications in numerous fields.
Multiple Approaches to Multiplication: Beyond the Basic Method
While the standard method of multiplication is straightforward, exploring alternative strategies enhances understanding and problem-solving skills. Let's examine some approaches for calculating 5 x 6 x 4:
-
Standard Multiplication: This involves multiplying two numbers at a time. We could start with 5 x 6 = 30, then multiply the result by 4: 30 x 4 = 120.
-
Associative Property: The associative property of multiplication states that the grouping of numbers does not affect the product. We can change the order of operations: (5 x 4) x 6 = 20 x 6 = 120, or (6 x 4) x 5 = 24 x 5 = 120. This demonstrates flexibility in calculations and can simplify the process.
-
Distributive Property: The distributive property allows us to break down multiplication into smaller, more manageable parts. For instance, we could rewrite 5 x 6 x 4 as 5 x (6 x 4) = 5 x 24 = 120, or even 5 x (6 x 2 x 2) which could be easier to solve mentally for some people. This is particularly useful when dealing with larger numbers.
-
Mental Math Techniques: Practicing mental math enhances mathematical fluency. For 5 x 6 x 4, we can leverage the fact that multiplying by 5 is equivalent to dividing by 2 and then multiplying by 10 (5 x 6 = 30; 30 x 4 = 120). Or we might break down 6 into 2 x 3 which can be multiplied in a series of smaller steps.
Real-World Applications of 5 x 6 x 4 and Volume Calculations
The concept of volume, and hence the calculation represented by 5 x 6 x 4, has a wide range of real-world applications across numerous disciplines:
-
Construction and Engineering: Calculating the volume of materials needed for construction projects (concrete, bricks, etc.) is crucial for accurate estimations and cost management. Imagine calculating the amount of concrete needed for a foundation – this directly involves volume calculations.
-
Packaging and Shipping: Businesses need to determine the volume of products to optimize packaging and shipping costs. Understanding the volume of a box helps in efficient space utilization.
-
Manufacturing: Calculating the volume of containers, storage tanks, and various components is essential in manufacturing processes. Precision in volume calculations is paramount in industries such as pharmaceuticals and food processing.
-
Agriculture: Estimating the volume of grain silos, water tanks, and other agricultural structures is crucial for efficient management of resources.
-
Medicine and Healthcare: Volume calculations are critical in administering medications, blood transfusions, and other medical procedures. Precise volume measurements are crucial for patient safety and treatment efficacy.
-
Environmental Science: Calculating the volume of pollutants in water bodies or the volume of land affected by natural disasters helps in environmental assessments and mitigation strategies.
Beyond Rectangular Prisms: Expanding Volume Calculations
While 5 x 6 x 4 directly relates to the volume of a rectangular prism, the principles extend to other three-dimensional shapes. The fundamental concept of multiplying three dimensions (length, width, and height, or analogous dimensions for other shapes) remains. However, more complex formulas are required for irregular shapes:
-
Cylinders: The volume of a cylinder is calculated using the formula: πr²h (where 'r' is the radius and 'h' is the height).
-
Spheres: The volume of a sphere is calculated using the formula: (4/3)πr³ (where 'r' is the radius).
-
Cones: The volume of a cone is calculated using the formula: (1/3)πr²h (where 'r' is the radius and 'h' is the height).
Understanding these formulas requires a deeper exploration of geometry, but the core principle of multiplying dimensions to determine volume remains consistent.
Addressing Common Misconceptions about Multiplication
Despite its apparent simplicity, multiplication can be a source of misconceptions, especially for younger learners. Let's address some common issues:
-
Order of Operations: The order in which we multiply numbers doesn't affect the final product (commutative property), but when combined with other operations (addition, subtraction, division), the order becomes crucial (following the BODMAS/PEMDAS rule).
-
Misunderstanding of Zero: Multiplying any number by zero always results in zero. This is a fundamental concept that needs to be clearly grasped.
-
Difficulty with Larger Numbers: As numbers get larger, multiplication can become more challenging. Breaking down larger numbers into smaller, more manageable parts using the distributive property can significantly aid calculations.
Frequently Asked Questions (FAQ)
-
Q: What is the answer to 5 x 6 x 4?
-
A: The answer is 120.
-
Q: Can I change the order of the numbers in 5 x 6 x 4?
-
A: Yes, due to the commutative and associative properties of multiplication, you can change the order without affecting the result. 5 x 6 x 4 = 5 x 4 x 6 = 6 x 5 x 4, and so on.
-
Q: What are some real-world uses of volume calculations beyond what's mentioned?
-
A: Volume calculations are also essential in fields like cooking (measuring ingredients), meteorology (calculating rainfall), and even astronomy (estimating the volume of celestial bodies).
-
Q: How can I improve my multiplication skills?
-
A: Consistent practice, exploring different multiplication methods, and utilizing mental math techniques are effective ways to improve your multiplication skills.
Conclusion: The Power of 5 x 6 x 4
The seemingly simple equation "5 x 6 x 4" offers a gateway to understanding fundamental mathematical concepts and their vast real-world applications. From calculating volumes to grasping the power of multiplication strategies, this equation underscores the importance of mathematical literacy in navigating the complexities of the world around us. By understanding its various interpretations and applications, we develop not only mathematical skills but also critical thinking and problem-solving abilities that extend far beyond the realm of numbers. Mastering basic mathematical concepts like this one is the foundation for tackling more complex challenges in various fields. Further exploration of these ideas and continued practice will solidify your mathematical foundation and unlock even greater opportunities for understanding and application.
Latest Posts
Latest Posts
-
Parts Of Speech Grammar Exercises
Sep 16, 2025
-
Consumer And Producer Surplus Definition
Sep 16, 2025
-
Voter Mobilization Definition Ap Gov
Sep 16, 2025
-
Unit 1 Ap World Test
Sep 16, 2025
-
Practice With Significant Figures Worksheet
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 5 X 6 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.