7 1/3 X 2 2/11
zacarellano
Sep 11, 2025 · 5 min read
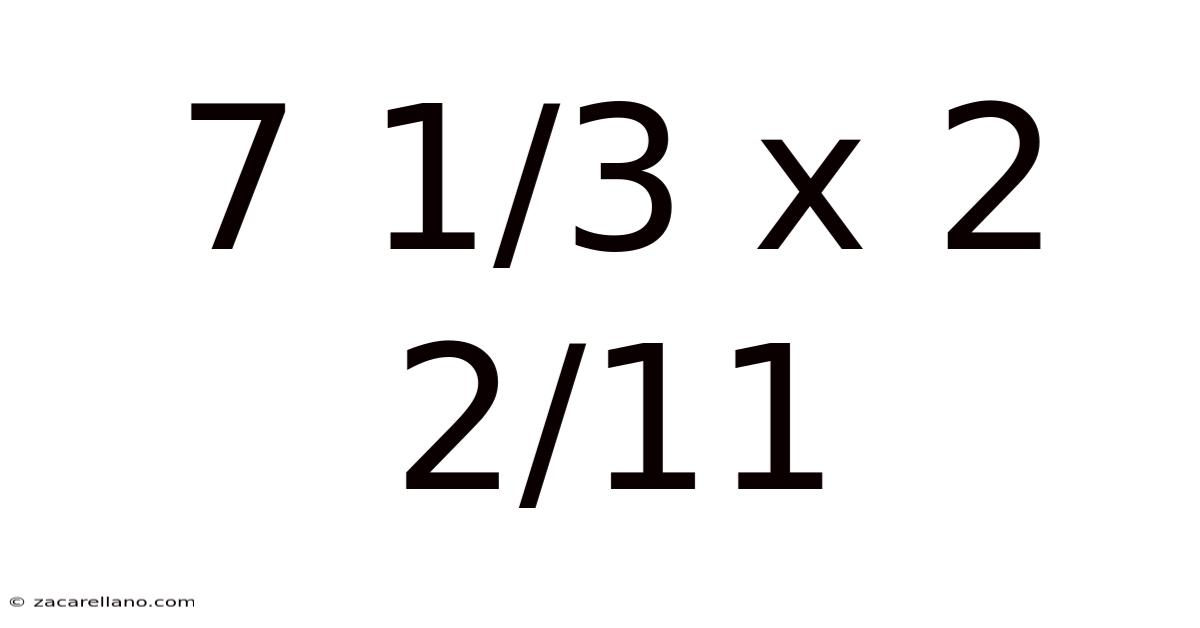
Table of Contents
Decoding the Mystery: A Deep Dive into 7 1/3 x 2 2/11
This article provides a comprehensive guide to solving the multiplication problem 7 1/3 x 2 2/11, going beyond a simple numerical answer to explore the underlying mathematical concepts. We'll break down the process step-by-step, explain the reasoning behind each step, and explore different methods for solving mixed number multiplication problems. Understanding this seemingly simple problem unlocks a deeper appreciation for fractions and their manipulation.
Introduction: Understanding Mixed Numbers and Multiplication
Before diving into the calculation of 7 1/3 x 2 2/11, let's refresh our understanding of mixed numbers and their role in multiplication. A mixed number combines a whole number and a fraction, like 7 1/3. This represents 7 whole units plus 1/3 of another unit. Multiplying mixed numbers requires converting them into a more manageable format, typically improper fractions. An improper fraction has a numerator larger than or equal to its denominator, such as 22/3. This conversion simplifies the multiplication process.
Step 1: Converting Mixed Numbers to Improper Fractions
To convert 7 1/3 to an improper fraction, we multiply the whole number (7) by the denominator (3) and add the numerator (1). This result (22) becomes the new numerator. The denominator remains the same (3). Therefore, 7 1/3 becomes 22/3.
Similarly, for 2 2/11, we multiply the whole number (2) by the denominator (11) and add the numerator (2). This gives us 24 as the new numerator, and the denominator remains 11. So, 2 2/11 transforms into 24/11.
Step 2: Multiplying the Improper Fractions
Now that we have converted our mixed numbers to improper fractions, we can multiply them directly:
(22/3) x (24/11)
To multiply fractions, we simply multiply the numerators together and the denominators together:
(22 x 24) / (3 x 11)
This gives us:
528 / 33
Step 3: Simplifying the Resulting Fraction
The fraction 528/33 is an improper fraction, and it's not in its simplest form. We need to simplify it by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD of 528 and 33 is 33. Dividing both the numerator and denominator by 33, we get:
528 ÷ 33 = 16 33 ÷ 33 = 1
Therefore, the simplified fraction is 16/1, which is equal to 16.
Step 4: The Final Answer
The solution to 7 1/3 x 2 2/11 is 16.
Alternative Methods: Exploring Different Approaches
While the above method is straightforward, let's explore alternative approaches to solving this problem, highlighting different mathematical skills.
Method 2: Distributive Property
The distributive property allows us to break down the multiplication into smaller, more manageable parts. We can rewrite the problem as:
(7 + 1/3) x (2 + 2/11)
Using the distributive property (FOIL method), we get:
(7 x 2) + (7 x 2/11) + (1/3 x 2) + (1/3 x 2/11)
This expands to:
14 + 14/11 + 2/3 + 2/33
Now, we need to find a common denominator for all fractions, which is 33. Converting all fractions to have a denominator of 33, we have:
14 + (14 x 3)/33 + (2 x 11)/33 + 2/33
This simplifies to:
14 + 42/33 + 22/33 + 2/33 = 14 + 66/33
Since 66/33 = 2, the final result is 14 + 2 = 16.
Method 3: Decimal Conversion
Another approach involves converting the mixed numbers into decimals before multiplying.
7 1/3 is approximately 7.333... 2 2/11 is approximately 2.1818...
Multiplying these decimal approximations:
7.333... x 2.1818... ≈ 16
This method provides an approximate answer due to the recurring decimals. It’s less precise than using fractions but offers a different perspective.
A Deeper Look: Understanding the Mathematics Behind the Steps
The seemingly simple act of multiplying mixed numbers involves several key mathematical concepts:
-
Fraction Conversion: Understanding how to convert between mixed numbers and improper fractions is fundamental. This skill is crucial for various mathematical operations involving fractions.
-
Multiplication of Fractions: The core of this problem lies in multiplying fractions. This involves multiplying the numerators and the denominators separately.
-
Simplification of Fractions: Reducing fractions to their simplest form is essential for clarity and efficiency. Finding the GCD allows us to express the fraction in its most concise representation.
-
Distributive Property: This property allows us to break down complex multiplications into simpler ones, providing flexibility in problem-solving.
-
Decimal Approximation: Although less precise, converting to decimals can be a useful tool, especially when dealing with complex fractions or needing a quick estimation.
Frequently Asked Questions (FAQ)
-
Why do we need to convert mixed numbers to improper fractions before multiplying? It simplifies the multiplication process. Multiplying improper fractions is a more straightforward process than dealing with the whole number and fractional parts separately.
-
What is the greatest common divisor (GCD)? The GCD is the largest number that divides evenly into two or more numbers. Finding the GCD is crucial for simplifying fractions.
-
Can I use a calculator to solve this? Yes, but understanding the underlying mathematical principles is more important than just getting the numerical answer. A calculator might give you a decimal approximation, while the fractional method provides a precise answer.
-
Are there other methods for solving this type of problem? Yes, there are numerous ways to approach this, each offering a unique understanding of the mathematical concepts involved. The methods discussed above are just a few examples.
Conclusion: Beyond the Numbers
Solving 7 1/3 x 2 2/11 is more than just finding the answer (16). It's about understanding the fundamental concepts of fractions, improper fractions, multiplication, simplification, and the distributive property. Mastering these concepts builds a strong foundation for more advanced mathematical topics. The different methods explored above highlight the flexibility and interconnectedness of mathematical principles. The key takeaway is not just the answer, but the journey of understanding and applying mathematical concepts to solve the problem. This problem serves as a microcosm of the broader mathematical landscape, demonstrating the power and elegance of mathematical thinking. By deeply understanding this seemingly simple equation, we build a more robust understanding of fundamental mathematical principles.
Latest Posts
Latest Posts
-
Henry David Thoreau Apush Definition
Sep 11, 2025
-
Sat Study Plan 3 Months
Sep 11, 2025
-
9 4 As A Decimal
Sep 11, 2025
-
Distribute And Combine Like Terms
Sep 11, 2025
-
Ap Computer Science Exam Questions
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 7 1/3 X 2 2/11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.