7/4 As A Mixed Number
zacarellano
Sep 24, 2025 · 6 min read
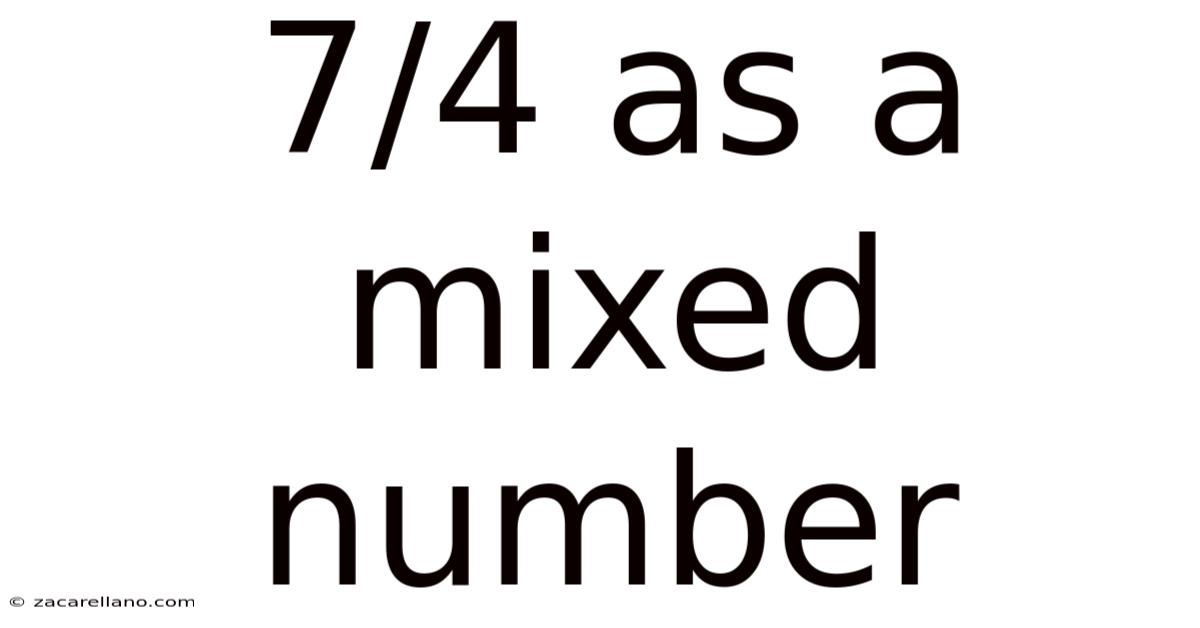
Table of Contents
Understanding 7/4 as a Mixed Number: A Comprehensive Guide
Fractions are fundamental building blocks in mathematics, and understanding how to represent them in different forms is crucial for mastering various mathematical concepts. This article delves deep into the representation of the improper fraction 7/4 as a mixed number, exploring the underlying concepts, providing step-by-step instructions, and addressing frequently asked questions. Learning to convert improper fractions to mixed numbers is essential for simplifying calculations and gaining a more intuitive grasp of fractional values. This guide will equip you with the skills and understanding necessary to confidently work with fractions in various mathematical contexts.
Introduction: What are Improper Fractions and Mixed Numbers?
Before we dive into converting 7/4, let's establish a clear understanding of the terms involved. An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). Examples include 7/4, 5/2, and 11/3. In essence, an improper fraction represents a value greater than or equal to one whole unit.
A mixed number, on the other hand, combines a whole number and a proper fraction. A proper fraction has a numerator smaller than its denominator (e.g., 1/2, 3/4, 2/5). Mixed numbers offer a more visually intuitive way to represent values greater than one. For instance, 1 ¾ represents one whole unit and three-quarters of another.
Converting 7/4 to a Mixed Number: A Step-by-Step Guide
Converting an improper fraction like 7/4 to a mixed number involves dividing the numerator by the denominator. Here's how it's done:
Step 1: Divide the Numerator by the Denominator
Divide 7 (the numerator) by 4 (the denominator).
7 ÷ 4 = 1 with a remainder of 3
Step 2: Identify the Whole Number and the Remainder
The result of the division gives us two key pieces of information:
- The quotient (1): This becomes the whole number part of the mixed number.
- The remainder (3): This becomes the numerator of the fractional part of the mixed number.
Step 3: Construct the Mixed Number
The denominator of the fraction remains the same as the denominator of the original improper fraction (4). Therefore, the mixed number representation of 7/4 is:
1 ³⁄₄
This means that 7/4 is equivalent to one and three-quarters.
Visualizing the Conversion: A Geometric Approach
Imagine you have seven equal-sized slices of pizza. Since each pizza typically has four slices, you have enough slices to make one whole pizza (four slices) and three slices remaining. This remaining three slices represent ¾ of a pizza. Therefore, you have 1 ¾ pizzas in total. This visual representation reinforces the concept of converting an improper fraction into a mixed number.
The Mathematical Explanation Behind the Conversion
The conversion from an improper fraction to a mixed number is based on the principle of partitioning or dividing the numerator into equal parts determined by the denominator. The division process essentially separates the whole units from the remaining fractional part. This process can be expressed algebraically:
-
Improper fraction: a/b (where 'a' is the numerator and 'b' is the denominator, and a ≥ b)
-
Division: a ÷ b = q with a remainder of r (where 'q' is the quotient and 'r' is the remainder)
-
Mixed number: q r/b
Working with Other Improper Fractions: Examples and Practice
Let's practice converting some other improper fractions to mixed numbers to solidify our understanding:
-
11/5: 11 ÷ 5 = 2 with a remainder of 1. Therefore, 11/5 = 2 ¹⁄₅
-
17/6: 17 ÷ 6 = 2 with a remainder of 5. Therefore, 17/6 = 2 ⁵⁄₆
-
9/2: 9 ÷ 2 = 4 with a remainder of 1. Therefore, 9/2 = 4 ¹⁄₂
-
23/8: 23 ÷ 8 = 2 with a remainder of 7. Therefore, 23/8 = 2 ⁷⁄₈
Remember, the key is to divide the numerator by the denominator, use the quotient as the whole number, and the remainder as the numerator of the fraction, keeping the original denominator.
Converting Mixed Numbers Back to Improper Fractions
It's equally important to understand the reverse process: converting a mixed number back to an improper fraction. This is useful for performing calculations involving mixed numbers. Here's how:
Step 1: Multiply the whole number by the denominator.
Step 2: Add the numerator to the result from Step 1.
Step 3: Keep the denominator the same.
Let's use the example of 1 ¾:
- 1 (whole number) × 4 (denominator) = 4
- 4 + 3 (numerator) = 7
- The improper fraction is therefore 7/4.
Applications of Improper Fractions and Mixed Numbers in Real Life
Improper fractions and mixed numbers are not just abstract mathematical concepts; they have practical applications in many real-life situations:
-
Cooking and Baking: Recipes often require fractional amounts of ingredients. Understanding improper fractions allows you to accurately measure and adjust recipes.
-
Construction and Engineering: Precise measurements are critical in construction and engineering. Mixed numbers are frequently used to represent dimensions and quantities.
-
Finance and Accounting: Fractions are used in calculations involving interest rates, shares, and other financial aspects.
-
Data Analysis: Fractions and mixed numbers are fundamental in data representation and analysis, especially when dealing with proportions and percentages.
Frequently Asked Questions (FAQs)
Q: What if the remainder is zero after dividing the numerator by the denominator?
A: If the remainder is zero, it means the improper fraction is a whole number. For example, 8/4 = 2 (because 8 ÷ 4 = 2 with a remainder of 0).
Q: Can I simplify the fractional part of a mixed number?
A: Yes, always simplify the fractional part of a mixed number to its lowest terms. For instance, 2 ⁶⁄₈ should be simplified to 2 ¾.
Q: Why is it important to learn how to convert between improper fractions and mixed numbers?
A: Converting between these forms allows for easier calculations, a clearer understanding of quantities, and better communication of fractional values in various contexts. It’s essential for further studies in algebra, geometry, and calculus.
Q: Are there any online tools or calculators that can help with this conversion?
A: While external tools are not permitted in this document, many online calculators can assist with the conversion of improper fractions to mixed numbers and vice-versa. These can be helpful for checking your work and building confidence.
Conclusion: Mastering Fractions for a Brighter Future
Understanding how to represent fractions in different forms, particularly the conversion between improper fractions and mixed numbers, is a critical skill in mathematics. This process isn’t just about manipulating numbers; it’s about developing a deeper understanding of numerical relationships and problem-solving abilities. By mastering this skill, you'll be better equipped to tackle more complex mathematical problems and apply these concepts in various real-world situations. The ability to confidently work with fractions is a cornerstone for success in higher-level mathematics and numerous other fields. Consistent practice and a solid grasp of the underlying principles will ensure your success in this important area of mathematics.
Latest Posts
Latest Posts
-
Are Chemical Bonds Potential Energy
Sep 24, 2025
-
Convert Z Score To Percentile
Sep 24, 2025
-
Ap Calculus Ab Optimization Problems
Sep 24, 2025
-
Balance Of Atoms Quick Check
Sep 24, 2025
-
Calcular El Area De Rectangulo
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 7/4 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.