7 Divided By 1 5
zacarellano
Sep 20, 2025 · 5 min read
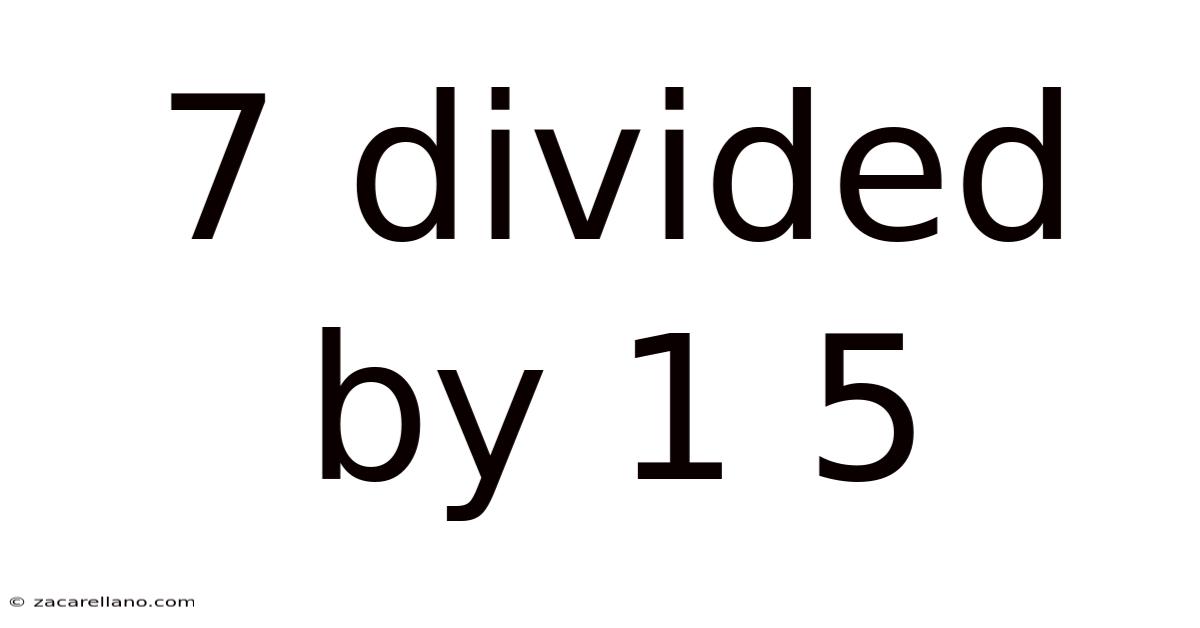
Table of Contents
Unveiling the Mystery: 7 Divided by 1.5
Dividing numbers can sometimes feel like navigating a maze, especially when decimals are involved. This article delves into the seemingly simple yet subtly complex problem of 7 divided by 1.5, providing a comprehensive understanding of the process, its underlying principles, and practical applications. We'll explore various methods to solve this problem, ensuring that even those with a basic understanding of mathematics can grasp the concept and confidently tackle similar divisions in the future. Understanding division with decimals is crucial for various fields, from everyday budgeting to advanced scientific calculations.
Introduction: Why 7 ÷ 1.5 Matters
The division of 7 by 1.5 (7 ÷ 1.5) might appear straightforward at first glance. However, the presence of a decimal divisor introduces a layer of complexity that warrants a detailed explanation. Mastering this type of calculation lays the foundation for more advanced mathematical operations and is essential for a firm grasp of numerical reasoning. This article aims to not just provide the answer but also illuminate the why behind the calculation, empowering you to solve similar problems independently. We'll explore different approaches, from long division to using fractions, providing a robust understanding of the underlying mathematical principles.
Method 1: Long Division
The traditional approach to solving 7 ÷ 1.5 involves long division. However, the presence of a decimal in the divisor requires an initial step to simplify the calculation. We can achieve this by multiplying both the dividend (7) and the divisor (1.5) by 10, effectively removing the decimal point.
-
Step 1: Eliminate the decimal: Multiply both 7 and 1.5 by 10. This gives us 70 ÷ 15.
-
Step 2: Perform long division: Now we can perform long division as follows:
4
15 | 70
-60
10
- Step 3: Express the remainder as a fraction or decimal: We have a remainder of 10. We can express this as a fraction (10/15) which simplifies to 2/3. Alternatively, we can continue the long division by adding a decimal point and a zero to the remainder, resulting in a decimal answer.
4.666...
15 | 70.000
-60
100
-90
100
-90
100
...
Therefore, 7 ÷ 1.5 = 4 and 2/3, or approximately 4.666... The repeating decimal 0.666... is equivalent to 2/3.
Method 2: Converting to Fractions
Another effective method involves converting the decimal divisor into a fraction. This approach often simplifies the calculation and provides a clear understanding of the underlying mathematical principles.
-
Step 1: Convert the decimal to a fraction: 1.5 can be expressed as the fraction 3/2.
-
Step 2: Rewrite the division as a multiplication of fractions: Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of 3/2 is 2/3. Therefore, the problem becomes 7 x (2/3).
-
Step 3: Perform the multiplication: Multiply the numerator (7 x 2 = 14) and keep the denominator (3). This results in the fraction 14/3.
-
Step 4: Convert the improper fraction to a mixed number: 14/3 is an improper fraction. To convert it to a mixed number, we divide 14 by 3. This gives us 4 with a remainder of 2. Therefore, 14/3 = 4 and 2/3.
Once again, we arrive at the same answer: 7 ÷ 1.5 = 4 and 2/3, or approximately 4.666...
Method 3: Using a Calculator
For practical purposes, especially when dealing with more complex calculations, a calculator is a useful tool. Simply input "7 ÷ 1.5" into your calculator to obtain the answer, which will likely be displayed as 4.666666... Remember that this is a repeating decimal, and the approximation will vary based on the calculator's precision.
Understanding the Decimal Result: Repeating Decimals
The result of 7 ÷ 1.5 is a repeating decimal (4.666...). This occurs when the division process does not result in a terminating decimal; the remainder continues indefinitely. Repeating decimals can be expressed as fractions, which often provides a more precise representation than a truncated decimal. In this case, the repeating decimal 0.666... is equivalent to the fraction 2/3.
Practical Applications: Real-World Scenarios
Understanding division with decimals, as illustrated by 7 ÷ 1.5, has numerous real-world applications:
- Budgeting: Calculating the number of items you can afford given a budget and the price per item.
- Cooking and Baking: Adjusting recipes based on the number of servings.
- Construction and Engineering: Calculating material quantities and dimensions.
- Science and Engineering: Numerous scientific calculations involve decimal division.
Frequently Asked Questions (FAQ)
-
Q: Why do we multiply both numbers by 10 in the long division method?
- A: Multiplying both the dividend and divisor by 10 (or a multiple of 10 depending on the decimal places) effectively removes the decimal from the divisor, simplifying the long division process. This doesn't change the result because we are essentially multiplying the entire fraction by 1 (10/10 = 1).
-
Q: What is the difference between a terminating and a repeating decimal?
- A: A terminating decimal has a finite number of digits after the decimal point (e.g., 2.5). A repeating decimal has a pattern of digits that repeats indefinitely (e.g., 4.666...).
-
Q: Can I use a different method to solve this problem?
- A: Yes, you can use various methods, including using a calculator or converting both numbers to fractions before dividing. The core principle remains the same – dividing 7 by 1.5.
-
Q: How can I express the answer as a fraction?
- A: The most accurate representation of the answer is 4 and 2/3. This avoids the limitations of representing the repeating decimal with a finite number of digits.
-
Q: Is there a way to avoid repeating decimals in such calculations?
- A: Not always. Many divisions involving decimals result in repeating decimals. The key is to understand how to represent them accurately, either as a fraction or using the appropriate number of significant figures depending on the context.
Conclusion: Mastering Decimal Division
Understanding 7 divided by 1.5 goes beyond simply obtaining the answer. It's about grasping the fundamental principles of division involving decimals, exploring different solution methods, and recognizing the implications of repeating decimals. By mastering these concepts, you'll enhance your mathematical skills and gain confidence in tackling more complex numerical problems in various fields of study and everyday life. Remember the flexibility of different methods – choose the one that best suits your understanding and the context of the problem. Whether you prefer long division, fraction conversion, or using a calculator, the core principle of division remains consistent and serves as a cornerstone of numerical reasoning.
Latest Posts
Latest Posts
-
Standard Form And Expanded Form
Sep 20, 2025
-
Unit 6 Test Algebra 1
Sep 20, 2025
-
Define A System In Physics
Sep 20, 2025
-
What Makes A Question Statistical
Sep 20, 2025
-
Linear Regression On Ti 84
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 7 Divided By 1 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.