8 25 As A Decimal
zacarellano
Sep 19, 2025 · 5 min read
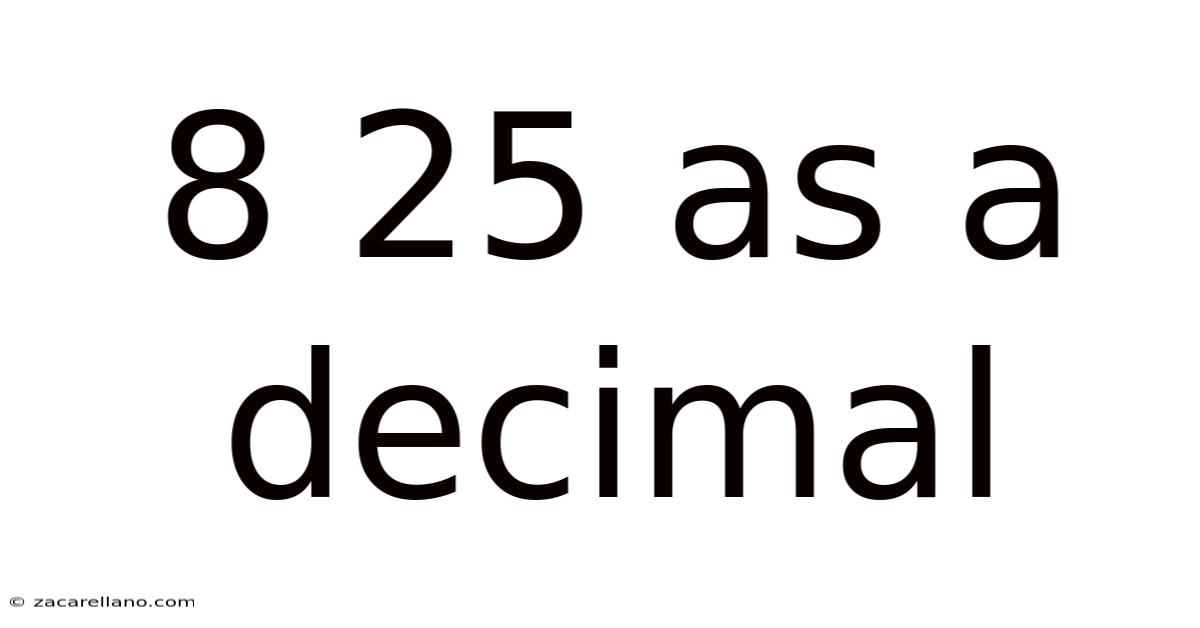
Table of Contents
8/25 as a Decimal: A Comprehensive Guide to Fraction-to-Decimal Conversion
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will explore the conversion of the fraction 8/25 to its decimal equivalent, explaining the process in detail and delving into the underlying principles. We'll cover various methods, address common misconceptions, and provide practical applications to solidify your understanding. By the end, you'll not only know that 8/25 is equal to 0.32 but also understand why and how to perform similar conversions confidently.
Understanding Fractions and Decimals
Before diving into the conversion, let's refresh our understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). A decimal is another way of expressing a part of a whole, using a base-ten system with a decimal point separating the whole number from the fractional part.
The fraction 8/25 means 8 parts out of a total of 25 parts. Our goal is to express this same quantity using the decimal system.
Method 1: Direct Division
The most straightforward method to convert a fraction to a decimal is through division. We simply divide the numerator by the denominator:
8 ÷ 25 = ?
Performing the division, we find:
8 ÷ 25 = 0.32
Therefore, 8/25 as a decimal is 0.32.
Method 2: Finding an Equivalent Fraction with a Denominator of 10, 100, 1000, etc.
This method involves manipulating the fraction to create an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, and so on). This is because any fraction with a denominator that is a power of 10 can be easily written as a decimal.
To convert 8/25 to an equivalent fraction with a denominator of 100, we need to multiply both the numerator and the denominator by the same number. Since 25 x 4 = 100, we multiply both the numerator and the denominator by 4:
(8 x 4) / (25 x 4) = 32/100
Now, 32/100 can be easily expressed as a decimal. The denominator, 100, indicates two decimal places. Therefore:
32/100 = 0.32
Method 3: Using Decimal Conversion Charts or Calculators
For quick conversions, especially when dealing with more complex fractions, you can utilize decimal conversion charts or calculators. These tools provide a convenient way to obtain the decimal equivalent of a fraction without performing manual calculations. Many scientific calculators and online converters offer this functionality. While convenient, understanding the underlying methods (like those described above) remains crucial for developing a strong mathematical foundation.
Understanding the Decimal Representation: Place Value
The decimal 0.32 represents thirty-two hundredths. Let's break down the place value:
- 0: Represents the whole number part (there are no whole numbers in this case).
- 3: Represents three tenths (3/10).
- 2: Represents two hundredths (2/100).
Therefore, 0.32 = 3/10 + 2/100 = 32/100, which is equivalent to 8/25.
Practical Applications of Fraction-to-Decimal Conversion
The ability to convert fractions to decimals is crucial in various real-world situations:
-
Financial Calculations: Percentages, interest rates, and discounts are often expressed as decimals. Converting fractions to decimals is essential for accurate financial calculations. For example, calculating a 8/25 discount on a $100 item requires converting 8/25 to 0.32, resulting in a discount of $32.
-
Measurement and Engineering: Many measurements in engineering and scientific fields involve both fractions and decimals. Converting between the two is necessary for accurate calculations and comparisons.
-
Data Analysis and Statistics: Data is often presented in both fractional and decimal formats. Converting between the two allows for easier analysis and interpretation of data.
-
Everyday Calculations: Simple everyday tasks like dividing a pizza equally among friends or calculating the cost of a purchase often involve fractions and decimals.
Common Misconceptions and Troubleshooting
-
Incorrect Division: Ensure you correctly divide the numerator by the denominator. A common mistake is reversing the order of division.
-
Decimal Place Value Errors: Pay close attention to the place value of each digit in the decimal representation. Misplacing the decimal point leads to incorrect results.
-
Incorrect Simplification: When using the equivalent fraction method, ensure you simplify the fraction to its lowest terms before converting it to a decimal.
Frequently Asked Questions (FAQ)
Q: Can all fractions be converted to terminating decimals?
A: No. Fractions with denominators that are not factors of powers of 10 (2, 5, 10, 20, 50, etc.) will result in repeating or non-terminating decimals. For example, 1/3 converts to 0.3333... (a repeating decimal).
Q: What if the decimal representation is very long?
A: For very long decimal representations, you can round to a certain number of decimal places based on the required level of accuracy.
Q: Are there other methods to convert fractions to decimals?
A: While the methods explained above are the most common, other advanced techniques exist, such as using continued fractions, but these are generally used in higher-level mathematics.
Q: Why is understanding this conversion important?
A: The ability to seamlessly move between fractions and decimals provides flexibility in solving problems and is a cornerstone of mathematical literacy. It enhances your problem-solving skills and opens doors to more complex mathematical concepts.
Conclusion
Converting 8/25 to a decimal is a straightforward process, illustrating a fundamental concept in mathematics. Whether you use direct division or the equivalent fraction method, the result remains the same: 0.32. This seemingly simple conversion holds significant practical value across diverse fields. Understanding the underlying principles and mastering this skill is essential for success in mathematics and its numerous applications in the real world. Remember, practice makes perfect, so continue to work through different fraction-to-decimal conversions to solidify your understanding and build confidence.
Latest Posts
Latest Posts
-
Miranda Rule Ap Gov Definition
Sep 19, 2025
-
30 60 90 Triangle Examples
Sep 19, 2025
-
How To Factor Big Polynomials
Sep 19, 2025
-
Crash Course Biology Cell Respiration
Sep 19, 2025
-
Craft Purple Pigment Dreamlight Valley
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 8 25 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.