D Dx Of Log X
zacarellano
Sep 15, 2025 · 7 min read
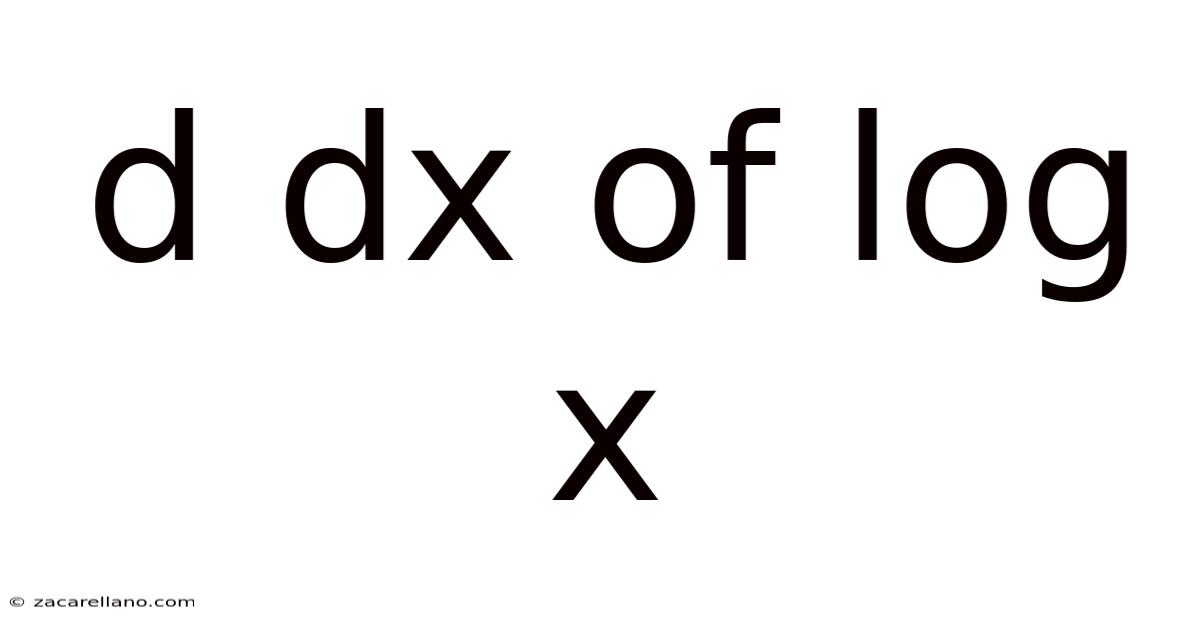
Table of Contents
Understanding d/dx of log x: A Comprehensive Guide
The derivative of the natural logarithm, often written as d/dx(ln x) or d/dx(logₑ x), is a fundamental concept in calculus with widespread applications in various fields, from physics and engineering to finance and economics. This comprehensive guide will explore this derivative in detail, explaining its derivation, applications, and addressing common misconceptions. Understanding this seemingly simple concept unlocks a deeper appreciation for logarithmic functions and their crucial role in mathematical modeling.
Introduction: The Natural Logarithm and its Properties
Before diving into the derivative, let's solidify our understanding of the natural logarithm. The natural logarithm, denoted as ln x or logₑ x, is the logarithm to the base e, where e is Euler's number, an irrational mathematical constant approximately equal to 2.71828. It's defined as the inverse function of the exponential function, eˣ. This means that if y = ln x, then x = eʸ.
Key properties of the natural logarithm are essential for understanding its derivative:
- ln(1) = 0: The natural logarithm of 1 is 0.
- ln(e) = 1: The natural logarithm of e is 1.
- ln(xy) = ln(x) + ln(y): The logarithm of a product is the sum of the logarithms.
- ln(x/y) = ln(x) - ln(y): The logarithm of a quotient is the difference of the logarithms.
- ln(xⁿ) = n ln(x): The logarithm of a number raised to a power is the power times the logarithm of the number.
Deriving d/dx(ln x) using the Definition of the Derivative
The derivative of a function, f(x), is defined as:
d/dx [f(x)] = lim (h→0) [(f(x + h) - f(x)) / h]
Applying this definition to f(x) = ln x, we get:
d/dx(ln x) = lim (h→0) [(ln(x + h) - ln(x)) / h]
Using the logarithmic property ln(a) - ln(b) = ln(a/b), we can simplify:
d/dx(ln x) = lim (h→0) [ln((x + h)/x) / h]
This can be further rewritten as:
d/dx(ln x) = lim (h→0) [ln(1 + h/x) / h]
Now, let's manipulate the expression. We can multiply and divide by x:
d/dx(ln x) = lim (h→0) [ln(1 + h/x) / (h/x)] * (1/x)
Let's substitute u = h/x. As h approaches 0, u also approaches 0. Therefore:
d/dx(ln x) = (1/x) * lim (u→0) [ln(1 + u) / u]
The limit lim (u→0) [ln(1 + u) / u] is a well-known limit in calculus, and its value is 1. This can be proven using L'Hôpital's rule or by considering the definition of the derivative of eˣ at x=0.
Therefore, we arrive at the final result:
d/dx(ln x) = 1/x
Understanding the Result: Geometric Interpretation and Applications
The derivative, 1/x, represents the instantaneous rate of change of the natural logarithm function at any point x. Geometrically, it's the slope of the tangent line to the curve y = ln x at a given point. Notice that the slope is always positive for x > 0, reflecting the increasing nature of the ln x function for positive x values. The slope approaches infinity as x approaches 0 from the right and approaches 0 as x approaches infinity.
The derivative d/dx(ln x) = 1/x has numerous applications:
- Solving differential equations: Many differential equations involving logarithmic functions can be solved using this derivative.
- Optimization problems: Finding maximum or minimum values of functions often involves calculating derivatives, and this result is crucial when logarithmic functions are involved.
- Economic modeling: Logarithmic functions are frequently used in economic models, such as Cobb-Douglas production functions, and their derivatives are essential for analyzing these models.
- Physics and engineering: Logarithmic scales and functions appear in various physical phenomena, and understanding their derivatives is crucial for modeling and analysis.
- Probability and statistics: The natural logarithm plays a significant role in probability distributions, such as the normal distribution, and its derivative is important in statistical calculations.
Derivative of logₓ(x) for other bases
While the natural logarithm (base e) has the simple derivative 1/x, the derivative of logarithms with other bases requires the change of base formula. Recall the change of base formula:
logₐ(b) = ln(b) / ln(a)
Therefore, logₓ(x) = ln(x) / ln(b)
Using the chain rule and the derivative of the natural logarithm, we find:
d/dx [logₓ(x)] = d/dx [ln(x) / ln(b)] = (1 / ln(b)) * (1/x) = 1 / (x ln(b))
This formula shows that the derivative of a logarithm with base b is a constant (1/ln(b)) times 1/x. When b = e, ln(b) = 1, and we recover the derivative of the natural logarithm.
Chain Rule and its Application with Logarithmic Derivatives
The chain rule is crucial when differentiating composite functions involving logarithms. The chain rule states that if we have a composite function y = f(g(x)), then its derivative is:
dy/dx = f'(g(x)) * g'(x)
For instance, consider the function y = ln(3x² + 1). Here, f(u) = ln(u) and g(x) = 3x² + 1. Applying the chain rule:
dy/dx = (1/(3x² + 1)) * (6x) = 6x / (3x² + 1)
This example illustrates how the chain rule simplifies the differentiation of more complex logarithmic functions.
Dealing with More Complex Scenarios: Implicit Differentiation and Logarithmic Differentiation
Sometimes, we encounter logarithmic functions within more intricate expressions. Implicit differentiation and logarithmic differentiation are powerful techniques to handle such cases.
Implicit Differentiation: If a logarithmic function is implicitly defined within an equation, we can use implicit differentiation to find its derivative. For example, consider x ln(y) + y = x. To find dy/dx, we differentiate both sides with respect to x, treating y as a function of x and using the product and chain rules.
Logarithmic Differentiation: Logarithmic differentiation is a useful technique for differentiating functions involving products, quotients, and powers of multiple terms. It involves taking the natural logarithm of both sides of an equation, simplifying using logarithmic properties, and then differentiating implicitly. For instance, consider y = (x² + 1)³(x + 2)⁴ / (x - 1)². Taking the natural logarithm simplifies the expression, allowing us to apply differentiation more efficiently.
Frequently Asked Questions (FAQ)
Q1: What is the difference between ln x and log x?
A1: ln x refers to the natural logarithm, which has base e. log x can refer to the common logarithm (base 10) or the logarithm with any other base unless the base is specified. The context usually clarifies the intended base.
Q2: Why is the natural logarithm so important?
A2: The natural logarithm has unique mathematical properties that make it particularly useful in calculus, and it appears naturally in many scientific and engineering applications. Its inverse function, the exponential function eˣ, has a derivative equal to itself, making it particularly useful for modeling exponential growth and decay processes.
Q3: Can the derivative of ln x be negative?
A3: No, the derivative of ln x, which is 1/x, is only defined for positive values of x. For x > 0, the derivative is always positive, reflecting the increasing nature of the function.
Q4: How do I differentiate a function like y = x^x?
A4: This requires logarithmic differentiation. Taking the natural logarithm of both sides, we get ln y = x ln x. Now, differentiating implicitly with respect to x using the product rule will give you the derivative.
Q5: What is the integral of 1/x?
A5: The indefinite integral of 1/x is ln|x| + C, where C is the constant of integration. The absolute value is necessary because the natural logarithm is only defined for positive arguments.
Conclusion
The derivative of the natural logarithm, d/dx(ln x) = 1/x, is a fundamental concept with widespread applications across various disciplines. Understanding its derivation, properties, and applications, along with mastering techniques like the chain rule, implicit differentiation, and logarithmic differentiation, unlocks a deeper appreciation of calculus and its power in modeling real-world phenomena. While the initial formula seems simple, its implications and broader applications within more complex mathematical contexts are far-reaching and essential for advanced studies in mathematics and its related fields. Remember to practice regularly to build your understanding and problem-solving skills. With consistent effort, you will become proficient in handling logarithmic derivatives and their various applications.
Latest Posts
Latest Posts
-
Logistic Growth Ap Calc Bc
Sep 15, 2025
-
How To Use Context Clues
Sep 15, 2025
-
Are All Unicellular Organisms Prokaryotes
Sep 15, 2025
-
Membrane Fluidity Is Affected By
Sep 15, 2025
-
Gcf Of 15 And 21
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about D Dx Of Log X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.