Derivative Of 3x 2 2
zacarellano
Sep 23, 2025 · 6 min read
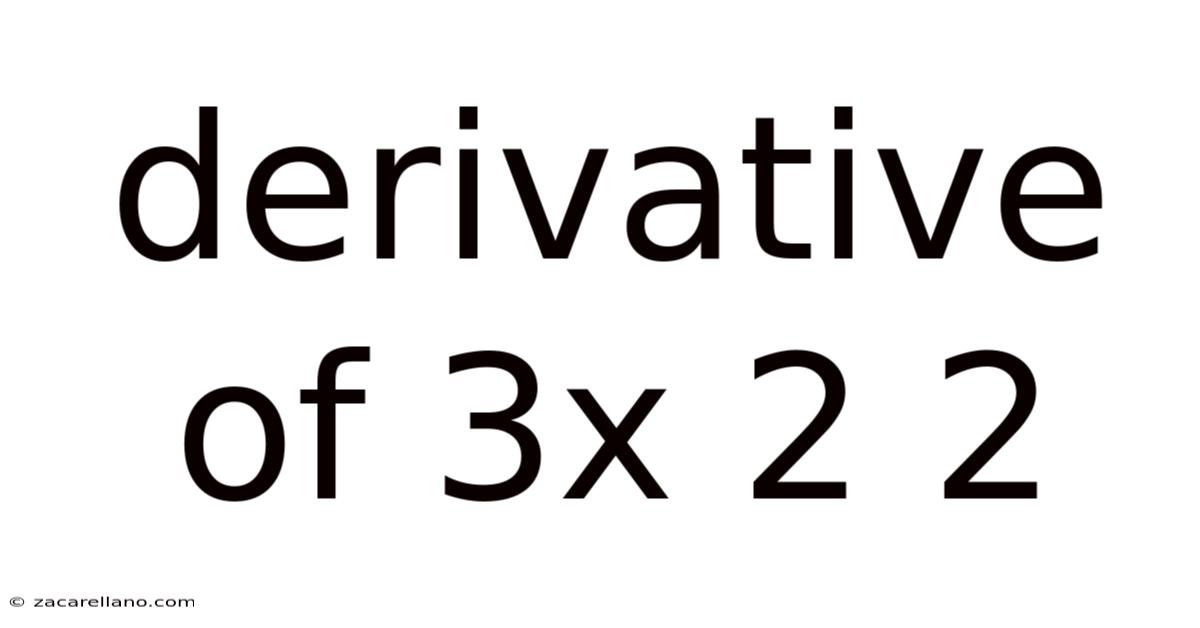
Table of Contents
Understanding the Derivative of 3x² + 2: A Comprehensive Guide
Finding the derivative of a function is a fundamental concept in calculus. It allows us to understand the instantaneous rate of change of a function at any given point. This article will provide a comprehensive explanation of how to find the derivative of the function f(x) = 3x² + 2, covering the underlying principles, step-by-step calculations, and practical applications. We will explore the power rule, constant rule, and the sum rule—essential tools in differential calculus. This guide is designed for students learning calculus for the first time, as well as those looking for a refresher on this important topic.
Introduction to Derivatives
The derivative of a function, denoted as f'(x) or df/dx, represents the instantaneous rate of change of the function at a specific point. Geometrically, it represents the slope of the tangent line to the curve of the function at that point. Understanding derivatives is crucial in various fields like physics (velocity and acceleration), economics (marginal cost and revenue), and engineering (optimization problems).
The process of finding a derivative is called differentiation. Several rules govern differentiation, and mastering these rules is key to successfully tackling more complex functions. For simpler functions like polynomials, the power rule is usually sufficient.
The Power Rule: A Cornerstone of Differentiation
The power rule is a fundamental theorem in calculus that simplifies the differentiation of functions of the form xⁿ, where n is a constant. The rule states that the derivative of xⁿ is nxⁿ⁻¹. Let's illustrate this:
- x²: The derivative is 2x¹ = 2x
- x³: The derivative is 3x²
- x⁴: The derivative is 4x³
And so on. This rule forms the basis for differentiating many polynomial functions.
The Constant Rule: Handling Constant Terms
The constant rule states that the derivative of a constant is always zero. This makes intuitive sense—a constant value doesn't change, so its rate of change is zero. For example:
- The derivative of 5 is 0
- The derivative of -10 is 0
- The derivative of π is 0
The Sum Rule: Differentiating Multiple Terms
The sum rule allows us to differentiate functions that are sums of other functions. It states that the derivative of a sum is the sum of the derivatives. In other words, if we have a function f(x) = g(x) + h(x), then f'(x) = g'(x) + h'(x).
Step-by-Step Differentiation of 3x² + 2
Now, let's apply these rules to find the derivative of our function, f(x) = 3x² + 2.
Step 1: Apply the Constant Multiple Rule
The function 3x² can be seen as a constant (3) multiplied by a function (x²). The constant multiple rule states that the derivative of cf(x) is c * f'(x), where c is a constant. Therefore, we can write:
d/dx (3x²) = 3 * d/dx (x²)
Step 2: Apply the Power Rule
Using the power rule, we find the derivative of x²:
d/dx (x²) = 2x
Step 3: Combine the Results
Substituting this back into our equation from Step 1:
d/dx (3x²) = 3 * 2x = 6x
Step 4: Apply the Constant Rule
The derivative of the constant term, 2, is 0.
d/dx (2) = 0
Step 5: Apply the Sum Rule
Finally, using the sum rule, we add the derivatives of each term:
d/dx (3x² + 2) = d/dx (3x²) + d/dx (2) = 6x + 0 = 6x
Therefore, the derivative of f(x) = 3x² + 2 is f'(x) = 6x.
Geometric Interpretation
The derivative, f'(x) = 6x, gives us the slope of the tangent line to the curve of y = 3x² + 2 at any point x. This means that for any given x-value, we can calculate the slope of the tangent at that point. For example:
- At x = 1, the slope is f'(1) = 6(1) = 6
- At x = 2, the slope is f'(2) = 6(2) = 12
- At x = 0, the slope is f'(0) = 6(0) = 0
This demonstrates how the slope of the tangent line changes as we move along the curve.
Higher-Order Derivatives
It's also possible to find higher-order derivatives. The second derivative, denoted as f''(x) or d²f/dx², represents the rate of change of the first derivative. In our example:
f'(x) = 6x
The second derivative is:
f''(x) = d/dx (6x) = 6
The third derivative would be 0, and all subsequent derivatives would also be 0.
Applications of Derivatives
The derivative of 3x² + 2, and more generally the concept of derivatives, has wide-ranging applications:
- Optimization: Finding maximum and minimum values of functions. For example, in business, finding the production level that maximizes profit.
- Related Rates: Solving problems where rates of change of different variables are related. For example, finding the rate at which the volume of a sphere is changing as its radius increases.
- Physics: Calculating velocity and acceleration. The derivative of position with respect to time gives velocity, and the derivative of velocity with respect to time gives acceleration.
- Economics: Determining marginal cost, marginal revenue, and marginal profit. These concepts are crucial in microeconomic analysis.
- Engineering: Designing optimal structures and systems.
Frequently Asked Questions (FAQ)
Q: What does it mean when the derivative is zero?
A: A derivative of zero indicates that the function is neither increasing nor decreasing at that point. It's a stationary point, which could be a local minimum, a local maximum, or a saddle point.
Q: Can we find the derivative of any function?
A: Not all functions are differentiable everywhere. Some functions may have points where the derivative is undefined (e.g., sharp corners or discontinuities).
Q: What if the function is more complex than a simple polynomial?
A: For more complex functions, we'll need to use other differentiation rules, such as the product rule, quotient rule, and chain rule, which are extensions of the basic rules we've covered. These rules enable us to differentiate functions involving products, quotients, and compositions of functions.
Q: How can I practice finding derivatives?
A: The best way to practice is to work through many examples. Start with simple polynomial functions, then gradually progress to more complex functions. Use online resources, textbooks, and practice problem sets to build your skills. Understanding the underlying principles is crucial for success.
Conclusion
Finding the derivative of 3x² + 2, which we determined to be 6x, is a straightforward application of fundamental calculus rules. This process, however, exemplifies the power and importance of differential calculus. Mastering the power rule, constant rule, and sum rule is foundational to understanding more complex differentiation techniques. The ability to calculate derivatives opens doors to solving diverse problems across various fields, making it a critical skill in mathematics and beyond. Remember to practice regularly and break down complex problems into smaller, manageable steps. With consistent effort and a strong grasp of the underlying principles, you will successfully navigate the world of derivatives.
Latest Posts
Latest Posts
-
Do T Rex Lay Eggs
Sep 23, 2025
-
Lcm Of 8 And 2
Sep 23, 2025
-
Hard To Balance Chemical Equations
Sep 23, 2025
-
Stages Of Sleep Ap Psychology
Sep 23, 2025
-
What Determines A Bond Length
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Derivative Of 3x 2 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.