Derive 1 1 X 2
zacarellano
Sep 23, 2025 · 5 min read
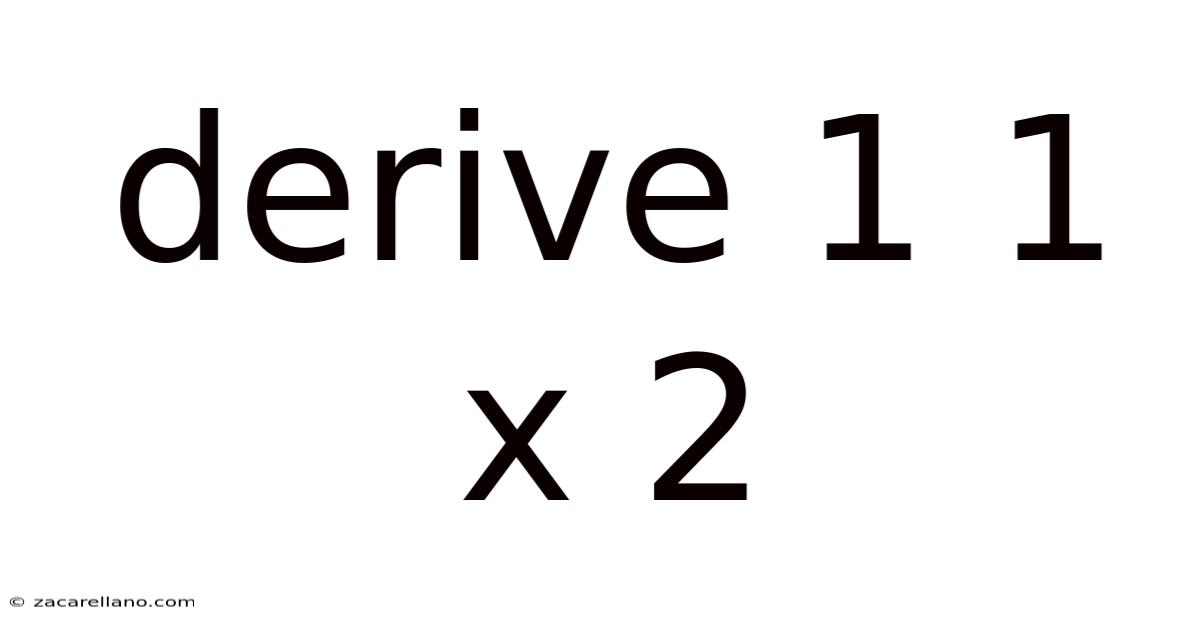
Table of Contents
Deriving the Formula: 1 + 1 x 2 = ? Understanding Order of Operations
This article explores the seemingly simple mathematical expression "1 + 1 x 2" and delves deep into the underlying principles governing its solution. We'll unravel the mystery behind the correct answer and explain why it's crucial to understand the order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). This seemingly basic equation is a gateway to understanding more complex algebraic manipulations and problem-solving skills.
Introduction: The Importance of Order of Operations
The expression "1 + 1 x 2" isn't just about getting the right numerical answer; it's about understanding the fundamental rules that govern mathematical calculations. Without a consistent order of operations, the result could vary depending on who's solving it, leading to chaos and inconsistency in mathematical computations. This is why learning and applying PEMDAS/BODMAS is vital, not just in elementary school, but throughout all levels of mathematics and beyond into fields like programming and engineering. This article will systematically break down the steps to solve this equation, explaining the reasoning behind each step and emphasizing the importance of consistent mathematical principles.
Step-by-Step Solution: Applying PEMDAS/BODMAS
The key to solving "1 + 1 x 2" correctly lies in applying the order of operations. Remember, PEMDAS/BODMAS dictates the sequence:
-
Parentheses/Brackets: These are operations enclosed in parentheses or brackets, and they take precedence over all other operations. In our equation, there are no parentheses.
-
Exponents/Orders: These involve powers and roots. Again, our equation lacks exponents.
-
Multiplication and Division: These operations have equal precedence and are performed from left to right. In "1 + 1 x 2," multiplication comes first: 1 x 2 = 2.
-
Addition and Subtraction: These operations also have equal precedence and are performed from left to right. After completing the multiplication, we have: 1 + 2 = 3.
Therefore, the correct answer to "1 + 1 x 2" is 3.
Why the Order Matters: Illustrating with Alternative Scenarios
Let's explore what would happen if we ignored the order of operations. If we were to perform the addition before the multiplication, we would get:
1 + 1 = 2 2 x 2 = 4
This gives us a completely different answer, which is incorrect. This example highlights the absolute necessity of following the established order of operations. Inconsistency in applying these rules will lead to inaccurate results, particularly as mathematical problems become more complex.
Beyond the Basics: Extending the Concept to More Complex Equations
The principle of PEMDAS/BODMAS extends far beyond simple equations like "1 + 1 x 2." Consider these more complex examples:
-
(2 + 3) x 4 - 5: Here, parentheses take precedence. First, we solve (2 + 3) = 5. Then, we perform the multiplication: 5 x 4 = 20. Finally, we subtract: 20 - 5 = 15. The answer is 15.
-
3² + (6 ÷ 2) x 5: This involves exponents, division, multiplication, and addition. Following PEMDAS/BODMAS, we start with the exponent: 3² = 9. Next, we perform the division: 6 ÷ 2 = 3. Then, the multiplication: 3 x 5 = 15. Finally, the addition: 9 + 15 = 24. The answer is 24.
These examples illustrate how understanding the order of operations is essential for accurately solving equations of increasing complexity. The same principles apply consistently, regardless of the complexity or the number of operations involved.
The Scientific and Programming Context: A Wider Perspective
The order of operations isn't merely a mathematical convention; it's a fundamental principle that underpins numerous scientific and technological applications. Programming languages, for instance, strictly adhere to a similar order of operations to ensure the consistent and predictable execution of code. A misunderstanding of this order can lead to errors in software and potentially even catastrophic failures in systems where precision is critical.
In scientific calculations, particularly in physics and engineering, the order of operations is paramount. Complex formulas and algorithms rely on the consistent application of these rules to produce accurate results. Whether calculating forces, velocities, or energy levels, adhering to PEMDAS/BODMAS is non-negotiable. Any deviation could lead to incorrect predictions and potentially dangerous consequences in real-world applications.
Addressing Common Misconceptions and Frequently Asked Questions (FAQ)
Many individuals, even those with some mathematical background, can occasionally stumble when faced with more complex equations. Let's address some common misconceptions:
-
Q: Does multiplication always come before addition? A: Yes, in the absence of parentheses or brackets, multiplication and division take precedence over addition and subtraction according to PEMDAS/BODMAS. However, multiplication and division are of equal precedence and are performed from left to right, and similarly for addition and subtraction.
-
Q: Why is the order of operations important? A: To ensure consistency and accuracy in mathematical calculations. Without a defined order, the result of an expression would depend on the individual performing the calculation.
-
Q: Are there any exceptions to PEMDAS/BODMAS? A: While PEMDAS/BODMAS provides a general framework, the context of the equation and the presence of specialized mathematical functions might require adjustments to the standard order. However, these exceptions are typically clearly defined within the context of advanced mathematics.
-
Q: What if I encounter a very long and complicated equation? A: Break the equation down into smaller, manageable parts. Focus on solving sections within parentheses first, then proceed according to the PEMDAS/BODMAS hierarchy.
-
Q: How do calculators handle the order of operations? Most modern scientific calculators automatically follow the PEMDAS/BODMAS rules. However, it's crucial to verify the correct use of parentheses to avoid ambiguities.
Conclusion: Mastering the Fundamentals
Understanding and correctly applying the order of operations, as represented by PEMDAS/BODMAS, is fundamental to success in mathematics and many other related fields. The seemingly simple equation "1 + 1 x 2" serves as a powerful illustration of this principle. While seemingly trivial, mastering this concept forms a solid foundation for tackling more complex mathematical problems, writing effective code, and understanding the underlying principles of numerous scientific applications. Remember, consistency and precision are paramount in the realm of mathematics, and the order of operations is the bedrock upon which this precision is built. By diligently practicing and applying this fundamental rule, you'll pave the way for success in your mathematical endeavors. The answer, 3, is not just a numerical result; it's a testament to the power of understanding the fundamental rules that govern our mathematical world.
Latest Posts
Latest Posts
-
A Positive Economic Statement Is
Sep 23, 2025
-
3x 2 5x 1 0
Sep 23, 2025
-
Is Ethanol Ionic Or Covalent
Sep 23, 2025
-
Evaluating Functions Worksheet Algebra 1
Sep 23, 2025
-
Mendel Called A Masking Trait
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Derive 1 1 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.