Gcf Of 12 And 27
zacarellano
Sep 19, 2025 · 6 min read
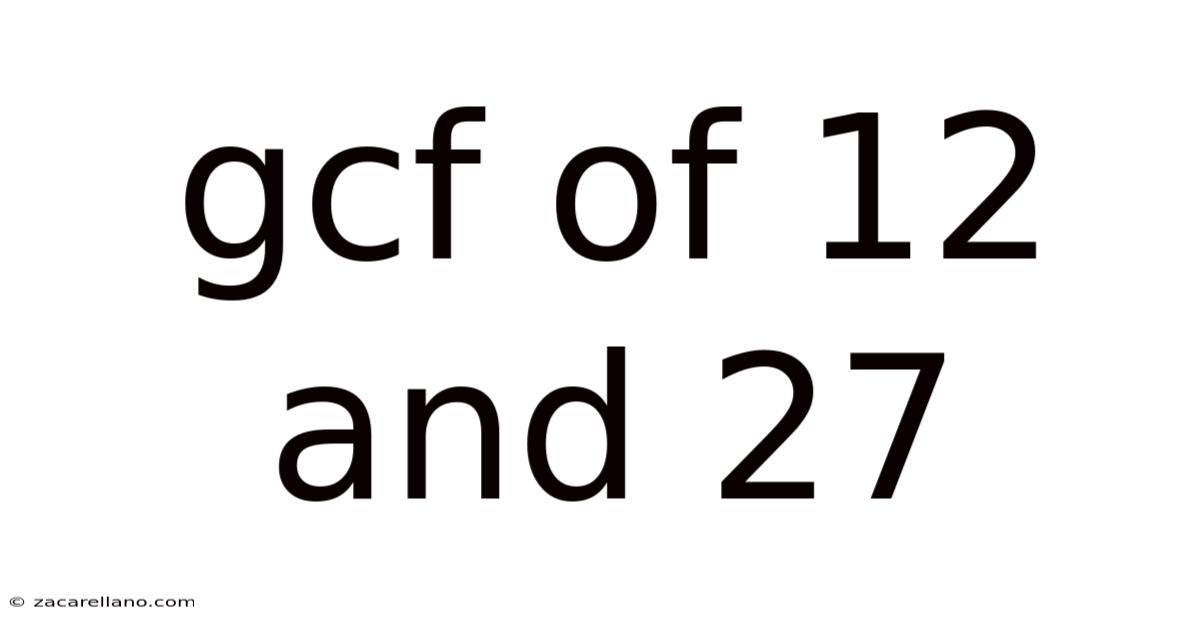
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 12 and 27: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles reveals a fascinating glimpse into number theory and its applications in various fields. This comprehensive guide delves into the methods of finding the GCF of 12 and 27, exploring different approaches and expanding upon the fundamental concepts involved. We'll move beyond simple calculation to understand why these methods work, laying a solid foundation for tackling more complex problems in number theory.
Understanding the Fundamentals: Factors and Divisors
Before diving into the GCF of 12 and 27, let's solidify our understanding of fundamental terms. A factor (or divisor) of a number is a whole number that divides evenly into that number without leaving a remainder. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12. Similarly, the factors of 27 are 1, 3, 9, and 27. The GCF is the largest factor that is common to both numbers.
Method 1: Listing Factors – A Simple, Intuitive Approach
The most straightforward method to find the GCF is by listing all the factors of each number and then identifying the largest common factor.
Factors of 12: 1, 2, 3, 4, 6, 12 Factors of 27: 1, 3, 9, 27
Comparing the two lists, we see that the common factors are 1 and 3. The largest of these common factors is 3. Therefore, the GCF of 12 and 27 is 3.
Method 2: Prime Factorization – A Powerful Technique for Larger Numbers
Prime factorization is a more efficient method, especially when dealing with larger numbers. This involves expressing each number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...).
Let's prime factorize 12 and 27:
- 12 = 2 x 2 x 3 = 2² x 3
- 27 = 3 x 3 x 3 = 3³
Now, identify the common prime factors and their lowest powers. Both 12 and 27 share the prime factor 3. The lowest power of 3 present in either factorization is 3¹ (or simply 3). Therefore, the GCF of 12 and 27 is 3.
Method 3: The Euclidean Algorithm – An Efficient Approach for Larger Numbers
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful when dealing with larger numbers where prime factorization becomes cumbersome. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 12 and 27:
- 27 – 12 = 15 (Now we find the GCF of 12 and 15)
- 15 – 12 = 3 (Now we find the GCF of 12 and 3)
- 12 – 3 – 3 – 3 – 3 = 0 (12 is divisible by 3).
Since we've reached a point where one number is divisible by the other without a remainder, the GCF is the smaller number, which is 3.
Why These Methods Work: A Deeper Look into Number Theory
The success of these methods hinges on fundamental concepts within number theory. The prime factorization method highlights the uniqueness of prime factorization – every number can be expressed as a unique product of primes. This uniqueness ensures that comparing the prime factorizations accurately identifies the common factors and thus, the GCF.
The Euclidean algorithm's efficacy is rooted in the properties of divisibility. Subtracting the smaller number from the larger number repeatedly maintains the GCF. This is because any common divisor of the original numbers will also be a divisor of their difference. This iterative process eventually leads to the GCF.
Applications of GCF in Real-World Scenarios
The GCF isn't just a theoretical concept; it finds practical applications in various fields:
-
Simplifying Fractions: Finding the GCF of the numerator and denominator allows for simplification of fractions to their lowest terms. For example, the fraction 12/27 simplifies to 4/9 by dividing both numerator and denominator by their GCF (3).
-
Geometry: The GCF is used in solving geometric problems involving dimensions and areas. For example, finding the largest square tile that can perfectly cover a rectangular area involves determining the GCF of the rectangle's length and width.
-
Project Management: Imagine needing to divide a project into equal tasks. If the total project time is 12 hours and the number of team members is 27, we can calculate a task schedule based on factors common to both. This method can improve team collaboration and avoid scheduling conflicts.
-
Cryptography: Number theory and concepts like GCF are fundamental to modern cryptography algorithms ensuring secure data transfer and storage.
Frequently Asked Questions (FAQ)
Q1: Is the GCF always less than the smaller of the two numbers?
Yes, the GCF is always less than or equal to the smaller of the two numbers. It cannot be larger, as it must be a common divisor.
Q2: What is the GCF of two prime numbers?
The GCF of two distinct prime numbers is always 1, as prime numbers only have 1 and themselves as factors.
Q3: Can the GCF of two numbers be zero?
No, the GCF cannot be zero. The GCF must be a positive integer that divides both numbers evenly.
Q4: What if one of the numbers is zero?
The GCF of any number and zero is undefined. The concept of factors doesn't apply consistently to zero. If considering only positive integers, some sources consider the GCF as the non-zero number.
Q5: How can I find the GCF of more than two numbers?
To find the GCF of more than two numbers, first find the GCF of any two of them, then find the GCF of that result and the next number, and so on.
Conclusion: Mastering the GCF – A Stepping Stone to Further Explorations
Finding the greatest common factor of 12 and 27, while seemingly simple, opens a window into the rich world of number theory. Understanding the different methods – listing factors, prime factorization, and the Euclidean algorithm – provides a solid foundation for tackling more complex numerical problems. The GCF is not merely a mathematical concept; it's a tool with practical applications across various disciplines, highlighting the interconnectedness of mathematics and the real world. By mastering this fundamental concept, you're not just solving a problem; you’re building a stronger mathematical intuition that serves as a stepping stone for more advanced studies in number theory and related fields. From simplifying fractions to contributing to advanced cryptography, the GCF's influence extends far beyond the initial arithmetic problem.
Latest Posts
Latest Posts
-
Gcf Of 21 And 15
Sep 19, 2025
-
Jazz Stars Of The 1920s
Sep 19, 2025
-
Y 2x 3 Standard Form
Sep 19, 2025
-
Ap Bio Dna Replication Diagram
Sep 19, 2025
-
Sin Graph Vs Cosine Graph
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 12 And 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.