Gcf Of 15 And 35
zacarellano
Sep 13, 2025 · 6 min read
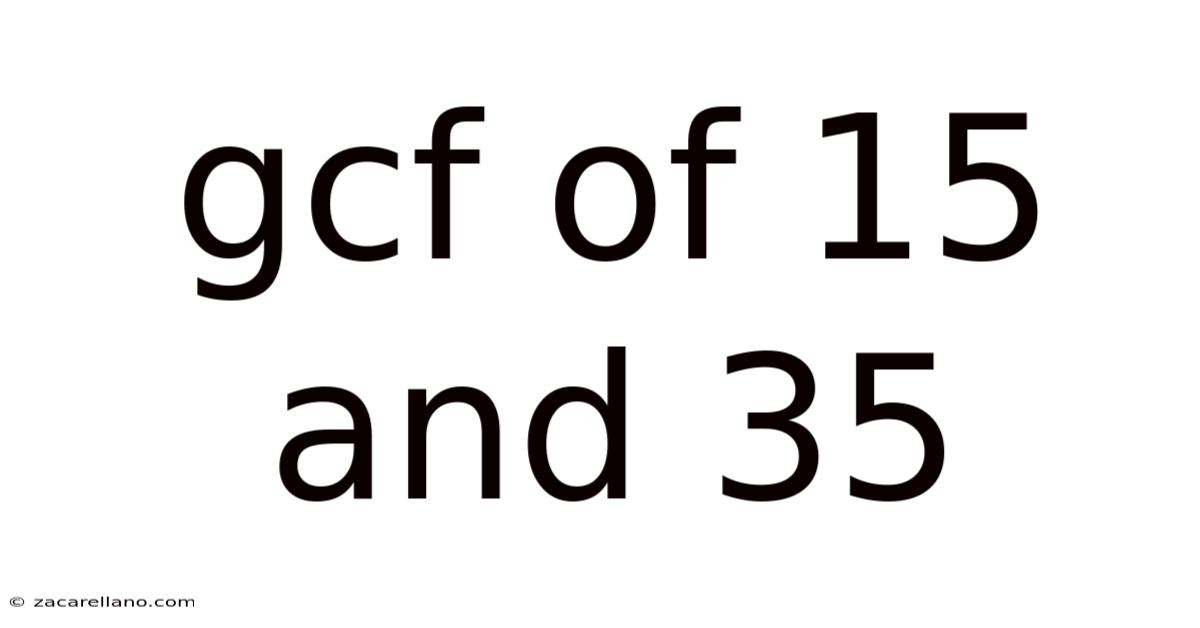
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 15 and 35: A Comprehensive Guide
Finding the Greatest Common Factor (GCF), also known as the Greatest Common Divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying concepts and different methods for calculating the GCF provides a strong foundation in number theory and its applications in various fields, from cryptography to computer science. This article will delve deep into finding the GCF of 15 and 35, exploring multiple approaches and explaining the mathematical principles involved. We'll also explore the broader significance of GCF and its practical uses.
Understanding the Concept of Greatest Common Factor (GCF)
The Greatest Common Factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6, so the GCF(12, 18) = 6.
Our focus here is on finding the GCF of 15 and 35. Let's explore several methods to achieve this.
Method 1: Listing Factors
This is the most straightforward method, especially for smaller numbers. We list all the factors of each number and then identify the largest factor common to both.
Factors of 15: 1, 3, 5, 15 Factors of 35: 1, 5, 7, 35
Comparing the lists, we see that the common factors are 1 and 5. The greatest of these common factors is 5. Therefore, the GCF(15, 35) = 5.
This method works well for small numbers, but becomes cumbersome and inefficient when dealing with larger numbers. Imagine trying to list all factors of 147 and 210! We need more efficient approaches.
Method 2: Prime Factorization
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers (primes are numbers greater than 1 divisible only by 1 and themselves). By expressing each number as a product of its prime factors, we can easily identify the GCF.
Prime factorization of 15: 3 x 5 Prime factorization of 35: 5 x 7
Both 15 and 35 contain the prime factor 5. Therefore, the GCF is the product of the common prime factors raised to the lowest power. In this case, the only common prime factor is 5, and its lowest power is 5<sup>1</sup> = 5. Hence, GCF(15, 35) = 5.
This method is more efficient than listing all factors, particularly for larger numbers. However, for extremely large numbers, finding the prime factorization can still be computationally intensive.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two integers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF. Let's illustrate this with 15 and 35:
- Start with the larger number (35) and the smaller number (15).
- Divide the larger number by the smaller number and find the remainder: 35 ÷ 15 = 2 with a remainder of 5.
- Replace the larger number with the smaller number (15) and the smaller number with the remainder (5).
- Repeat the process: 15 ÷ 5 = 3 with a remainder of 0.
- Since the remainder is 0, the GCF is the last non-zero remainder, which is 5.
Therefore, GCF(15, 35) = 5.
The Euclidean algorithm is remarkably efficient, even for very large numbers, because it significantly reduces the size of the numbers involved in each step. It forms the basis of many GCF-related algorithms in computer science.
A Deeper Dive into Prime Factorization and its Significance
The prime factorization method highlights the fundamental role of prime numbers in number theory. Prime numbers are the building blocks of all integers, and understanding their properties is crucial for various mathematical and computational tasks.
Prime factorization, while seemingly simple, has significant implications:
- Cryptography: The difficulty of factoring large numbers into their prime components is the foundation of many modern encryption algorithms, such as RSA. The security of online transactions and data protection relies heavily on this computational challenge.
- Modular Arithmetic: Prime factorization is essential in modular arithmetic, a branch of number theory used extensively in cryptography and computer science. Understanding prime factorization allows for efficient computations within modular systems.
- Number Theory Research: Prime factorization remains an active area of research. New algorithms and discoveries continue to refine our understanding of primes and their distribution.
Applications of GCF in Real-World Scenarios
The concept of GCF isn't limited to theoretical mathematics. It finds practical applications in various situations:
- Simplifying Fractions: Finding the GCF is essential for simplifying fractions to their lowest terms. For example, to simplify the fraction 15/35, we find the GCF(15, 35) = 5, and divide both the numerator and denominator by 5, resulting in the simplified fraction 3/7.
- Dividing Objects Equally: Imagine you have 15 apples and 35 oranges, and you want to divide them into identical bags, with the same number of apples and oranges in each bag. The GCF(15, 35) = 5 tells you that you can create 5 identical bags, each containing 3 apples and 7 oranges.
- Measurement and Geometry: GCF is used in solving problems related to measurements and geometry, such as finding the largest square tile that can perfectly cover a rectangular floor.
Frequently Asked Questions (FAQ)
-
Q: Is the GCF always smaller than the two numbers?
A: Yes, the GCF is always less than or equal to the smaller of the two numbers. It cannot be larger because it must divide both numbers without a remainder.
-
Q: What is the GCF of two prime numbers?
A: The GCF of two distinct prime numbers is always 1. Since prime numbers are only divisible by 1 and themselves, they have no common factors other than 1.
-
Q: What if I have more than two numbers? How do I find the GCF?
A: You can extend any of the methods discussed (prime factorization or Euclidean algorithm) to find the GCF of multiple numbers. For prime factorization, you would find the prime factorization of each number and identify the common prime factors raised to the lowest power. For the Euclidean algorithm, you would find the GCF of two numbers at a time, iteratively.
Conclusion
Finding the GCF of 15 and 35, while seemingly a simple exercise, offers a valuable gateway to understanding fundamental concepts in number theory. We’ve explored several methods – listing factors, prime factorization, and the Euclidean algorithm – each with its own strengths and weaknesses. The Euclidean algorithm emerges as the most efficient method, especially for larger numbers. Beyond the calculation itself, understanding the GCF provides insight into the structure of numbers and their applications in various fields, highlighting the interconnectedness of seemingly disparate areas of mathematics and its practical relevance in our daily lives. The seemingly simple concept of the greatest common factor unveils a deeper world of mathematical principles and practical applications.
Latest Posts
Latest Posts
-
2 X 1 Digit Multiplication
Sep 13, 2025
-
Newman Projections Pratice With Answers
Sep 13, 2025
-
Formula Del Area De Rectangulo
Sep 13, 2025
-
Find Normal Vector Of Plane
Sep 13, 2025
-
Light Work No Reaction Meaning
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 15 And 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.