Gcf Of 16 And 12
zacarellano
Sep 12, 2025 · 7 min read
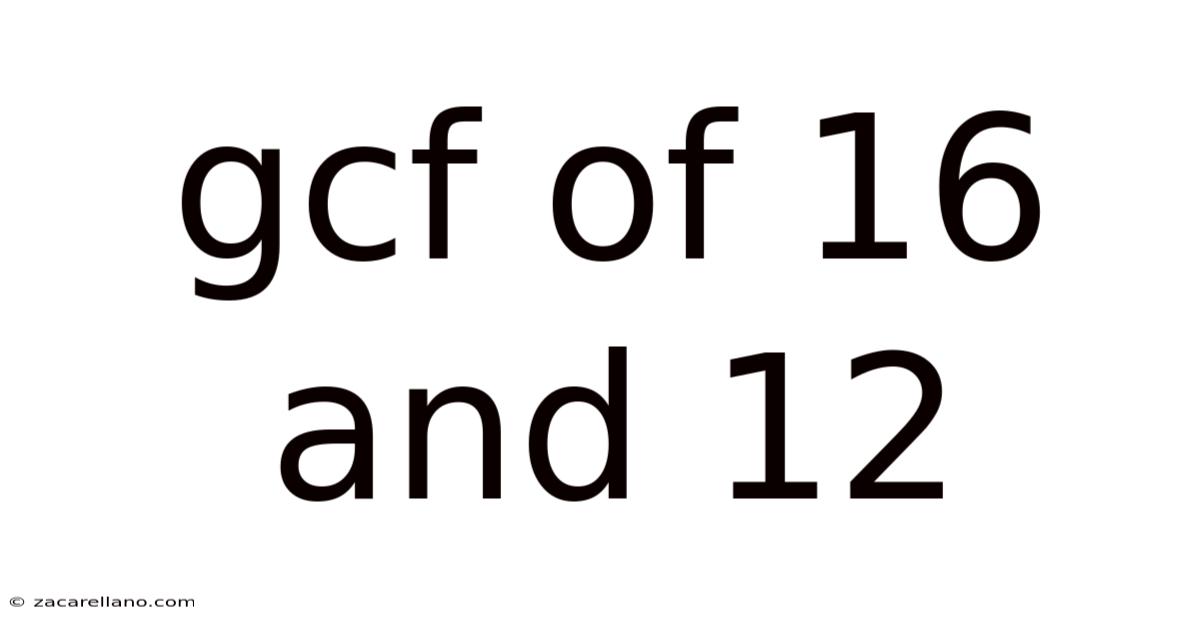
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 16 and 12: A Deep Dive
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles and exploring different methods for calculating the GCF opens up a world of mathematical concepts with broader applications in algebra, number theory, and even computer science. This article will delve into the GCF of 16 and 12, exploring multiple approaches to finding the answer and expanding on the significance of this fundamental concept. We'll cover everything from basic methods to more advanced techniques, ensuring a comprehensive understanding for all levels.
Understanding the Greatest Common Factor (GCF)
Before we jump into calculating the GCF of 16 and 12, let's establish a solid foundation. The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that perfectly divides both numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 16 are 1, 2, 4, 8, and 16. The common factors of 12 and 16 are 1, 2, and 4. The greatest among these is 4, hence the GCF of 12 and 16 is 4.
Method 1: Listing Factors
This is the most straightforward method, particularly useful for smaller numbers. We list all the factors of each number and then identify the largest common factor.
Factors of 12: 1, 2, 3, 4, 6, 12 Factors of 16: 1, 2, 4, 8, 16
Common Factors: 1, 2, 4
Greatest Common Factor (GCF): 4
This method is simple and intuitive, making it ideal for beginners. However, it becomes less efficient when dealing with larger numbers, as listing all factors can be time-consuming and prone to errors.
Method 2: Prime Factorization
This method involves breaking down each number into its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...). The prime factorization of a number is expressing it as a product of its prime factors.
Prime Factorization of 12:
12 = 2 x 2 x 3 = 2² x 3
Prime Factorization of 16:
16 = 2 x 2 x 2 x 2 = 2⁴
Now, we identify the common prime factors and their lowest powers. Both 12 and 16 have 2 as a prime factor. The lowest power of 2 present in both factorizations is 2².
Therefore, the GCF of 12 and 16 is 2² = 4.
This method is more efficient than listing factors, especially for larger numbers, as it systematically breaks down the numbers into their fundamental building blocks.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to find the GCF of 16 and 12:
- Start with the larger number (16) and the smaller number (12).
- Divide the larger number by the smaller number and find the remainder: 16 ÷ 12 = 1 with a remainder of 4.
- Replace the larger number with the smaller number (12) and the smaller number with the remainder (4).
- Repeat the process: 12 ÷ 4 = 3 with a remainder of 0.
- Since the remainder is 0, the GCF is the last non-zero remainder, which is 4.
The Euclidean algorithm is significantly more efficient than the previous methods for large numbers because it avoids the need to find all factors. Its efficiency makes it a cornerstone algorithm in various computational applications.
Understanding the Significance of GCF
The GCF is not merely a mathematical curiosity; it has numerous practical applications across various fields:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. To simplify a fraction, divide both the numerator and the denominator by their GCF. For example, the fraction 12/16 can be simplified to 3/4 by dividing both the numerator and denominator by their GCF, which is 4.
-
Solving Problems Involving Ratios and Proportions: The GCF helps to simplify ratios and proportions, making them easier to understand and work with.
-
Geometry and Measurement: The GCF is used in geometric problems involving finding the dimensions of shapes or determining the greatest common measure of lengths. For instance, if you have two pieces of wood, one 12 inches long and the other 16 inches long, the GCF (4 inches) helps determine the largest possible square tile that can be used to cover both pieces without any leftover tile.
-
Number Theory and Cryptography: The GCF plays a vital role in number theory, particularly in the study of prime numbers and modular arithmetic. It is also a fundamental element in cryptographic algorithms that secure digital communications.
-
Computer Science: The Euclidean algorithm, a primary method for computing the GCF, is used extensively in computer science for various applications, including cryptography and computer graphics.
Beyond the Basics: Extending the Concept
The concept of the GCF extends beyond just two numbers. We can find the GCF of three or more numbers by applying the same principles. For example, to find the GCF of 12, 16, and 20, we can use prime factorization or the Euclidean algorithm iteratively.
Prime Factorization Method:
- 12 = 2² x 3
- 16 = 2⁴
- 20 = 2² x 5
The common prime factor is 2, and the lowest power is 2². Therefore, the GCF of 12, 16, and 20 is 4.
Euclidean Algorithm (iterative):
- Find the GCF of 12 and 16 (which is 4).
- Find the GCF of 4 and 20 (which is 4).
Therefore, the GCF of 12, 16, and 20 is 4.
Frequently Asked Questions (FAQ)
Q1: What is the difference between GCF and LCM?
A1: The GCF (Greatest Common Factor) is the largest number that divides both numbers without a remainder. The LCM (Least Common Multiple) is the smallest number that is a multiple of both numbers. They are related inversely; for two numbers a and b, GCF(a, b) x LCM(a, b) = a x b.
Q2: Can the GCF of two numbers be 1?
A2: Yes, if two numbers have no common factors other than 1, their GCF is 1. Such numbers are called relatively prime or coprime. For example, the GCF of 15 and 28 is 1.
Q3: How can I use the GCF to simplify fractions?
A3: To simplify a fraction, find the GCF of the numerator and the denominator. Then divide both the numerator and denominator by the GCF. The resulting fraction will be in its simplest form.
Q4: Is there a limit to how large the GCF can be?
A4: The GCF of two numbers cannot be larger than the smaller of the two numbers.
Q5: Are there any online calculators or tools to find the GCF?
A5: Yes, many online calculators and mathematical software packages can quickly compute the GCF of any two or more numbers.
Conclusion
Finding the greatest common factor of 16 and 12, which is 4, is a seemingly simple task, but it reveals a deeper understanding of fundamental mathematical concepts. Through various methods like listing factors, prime factorization, and the Euclidean algorithm, we've explored different approaches to solve this problem, highlighting the efficiency and versatility of each method. Understanding the GCF is crucial not only for basic arithmetic but also for advanced mathematical applications in various fields, emphasizing its importance in mathematics and beyond. The ability to calculate the GCF effectively is a valuable skill that extends far beyond the classroom, applicable to problem-solving in diverse areas. This exploration of the GCF serves as a stepping stone to more complex mathematical concepts and their practical relevance in our world.
Latest Posts
Latest Posts
-
A Negative Plus Negative Equals
Sep 12, 2025
-
Volume Of Trapezoidal Prism Calculator
Sep 12, 2025
-
Ap Biology Unit 6 Test
Sep 12, 2025
-
Behind The Gare Saint Lazare
Sep 12, 2025
-
Alteration Of Generation In Plants
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 16 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.