Gcf Of 16 And 9
zacarellano
Sep 17, 2025 · 6 min read
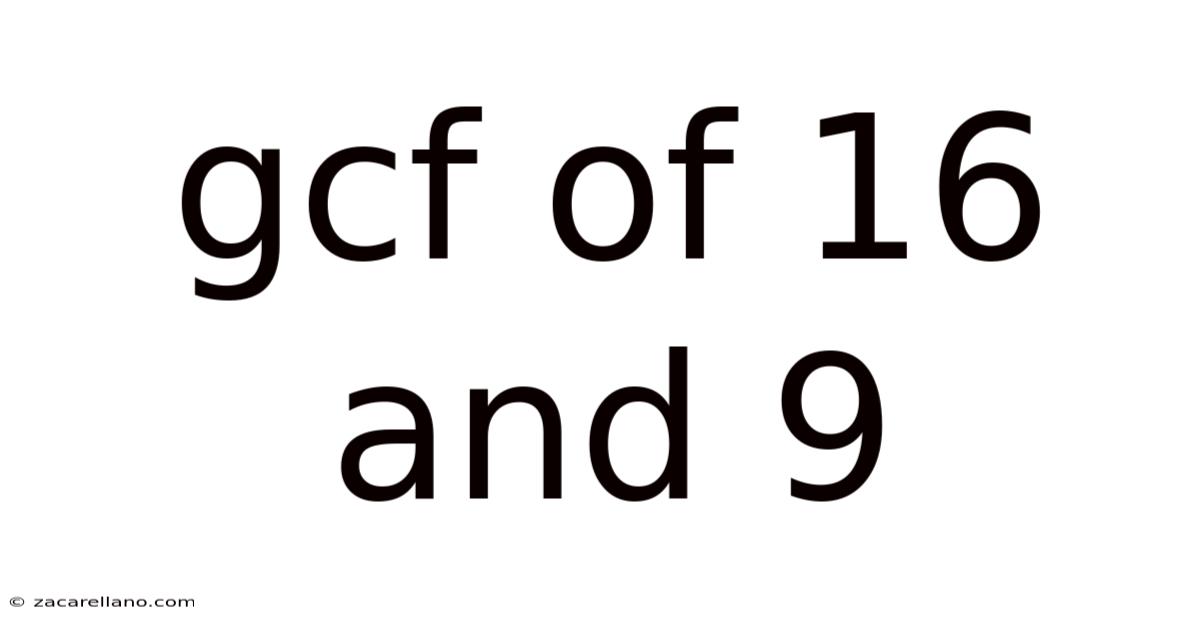
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 16 and 9: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles and various methods for determining the GCF opens doors to a deeper appreciation of number theory and its applications in various fields, from cryptography to computer science. This comprehensive guide will explore the GCF of 16 and 9, explaining multiple approaches and delving into the theoretical foundations. We'll move beyond a simple answer to illuminate the rich mathematical landscape surrounding this fundamental concept.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder. Understanding the GCF is crucial for simplifying fractions, solving algebraic equations, and many other mathematical operations.
Finding the GCF of 16 and 9: Method 1 – Listing Factors
The most straightforward method to find the GCF is by listing all the factors of each number and identifying the largest common factor.
Factors of 16: 1, 2, 4, 8, 16 Factors of 9: 1, 3, 9
Comparing the two lists, we see that the only common factor is 1. Therefore, the GCF of 16 and 9 is 1.
Finding the GCF of 16 and 9: Method 2 – Prime Factorization
Prime factorization involves expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. This method is particularly useful for larger numbers.
- Prime factorization of 16: 2 x 2 x 2 x 2 = 2⁴
- Prime factorization of 9: 3 x 3 = 3²
Since there are no common prime factors between 16 and 9, their GCF is 1. This confirms the result obtained using the previous method.
Finding the GCF of 16 and 9: Method 3 – Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 16 and 9:
- 16 ÷ 9 = 1 with a remainder of 7. We replace 16 with 7.
- 9 ÷ 7 = 1 with a remainder of 2. We replace 9 with 2.
- 7 ÷ 2 = 3 with a remainder of 1. We replace 7 with 1.
- 2 ÷ 1 = 2 with a remainder of 0. The process stops here.
The last non-zero remainder is 1, so the GCF of 16 and 9 is 1. The Euclidean algorithm provides a systematic and efficient way to determine the GCF, even for very large numbers.
Relatively Prime Numbers: The Significance of GCF = 1
When the GCF of two numbers is 1, as in the case of 16 and 9, the numbers are called relatively prime or coprime. This means that they share no common factors other than 1. Relatively prime numbers have several important properties and applications in various areas of mathematics and computer science. For example:
- Fraction Simplification: If the numerator and denominator of a fraction are relatively prime, the fraction is in its simplest form.
- Modular Arithmetic: Relatively prime numbers play a crucial role in modular arithmetic, a branch of number theory used in cryptography and computer science.
- Number Theory: The concept of relatively prime numbers is fundamental to various theorems and proofs in number theory.
Further Exploration: GCF and LCM
The greatest common factor (GCF) is closely related to the least common multiple (LCM). The LCM of two numbers is the smallest positive integer that is a multiple of both numbers. There's a useful relationship between the GCF and LCM of two numbers:
Product of two numbers = GCF x LCM
For 16 and 9:
- Product of 16 and 9 = 144
- GCF of 16 and 9 = 1
- Therefore, LCM of 16 and 9 = 144 / 1 = 144
This relationship provides a convenient way to find the LCM if the GCF is known, and vice versa.
Applications of GCF in Real-World Scenarios
While the concept might seem purely theoretical, the GCF has practical applications in various real-world scenarios:
- Dividing Objects: Imagine you have 16 apples and 9 oranges, and you want to divide them into equal groups without any leftovers. The GCF (which is 1 in this case) indicates that you can only make groups of one.
- Simplifying Fractions: When simplifying fractions, finding the GCF of the numerator and denominator allows you to reduce the fraction to its simplest form. For example, if you have the fraction 16/24, finding the GCF (which is 8) allows you to simplify it to 2/3.
- Project Management: In project scheduling, determining the GCF of various project durations can help in optimizing resource allocation and minimizing idle time.
- Music Theory: GCF is used in music theory to find the greatest common divisor of note durations, which is crucial in understanding rhythmic complexity and creating harmonious compositions.
Frequently Asked Questions (FAQ)
- Q: Is the GCF always 1? A: No, the GCF can be any positive integer. It's only 1 when the numbers are relatively prime.
- Q: What if I have more than two numbers? A: The same methods (prime factorization and the Euclidean algorithm) can be extended to find the GCF of more than two numbers.
- Q: Why is the Euclidean algorithm efficient? A: The Euclidean algorithm is efficient because it reduces the size of the numbers involved in each step, converging quickly to the GCF.
- Q: Are there any other methods to find the GCF? A: Yes, there are more advanced algorithms, particularly useful for very large numbers, including those based on modular arithmetic. These are typically beyond the scope of introductory number theory.
Conclusion
Determining the GCF of 16 and 9, while seemingly straightforward, serves as a gateway to understanding fundamental concepts in number theory. By exploring various methods, including listing factors, prime factorization, and the Euclidean algorithm, we've not only found the GCF (which is 1) but also grasped the broader significance of relatively prime numbers and their applications in different fields. This exploration should foster a deeper appreciation for the elegance and power of mathematics and its profound influence on our understanding of the world around us. Understanding the GCF is not just about finding a single answer; it's about mastering a key concept that unlocks a deeper understanding of numerical relationships and their implications in various areas of study and application.
Latest Posts
Latest Posts
-
Adding And Subtracting In Kindergarten
Sep 17, 2025
-
Is It Pemdas Or Pedmas
Sep 17, 2025
-
How To Calculate Matching Distance
Sep 17, 2025
-
Cuantos Minutos Tiene Una Hora
Sep 17, 2025
-
How To Find Rhombus Diagonals
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 16 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.