Gcf Of 18 And 54
zacarellano
Sep 18, 2025 · 5 min read
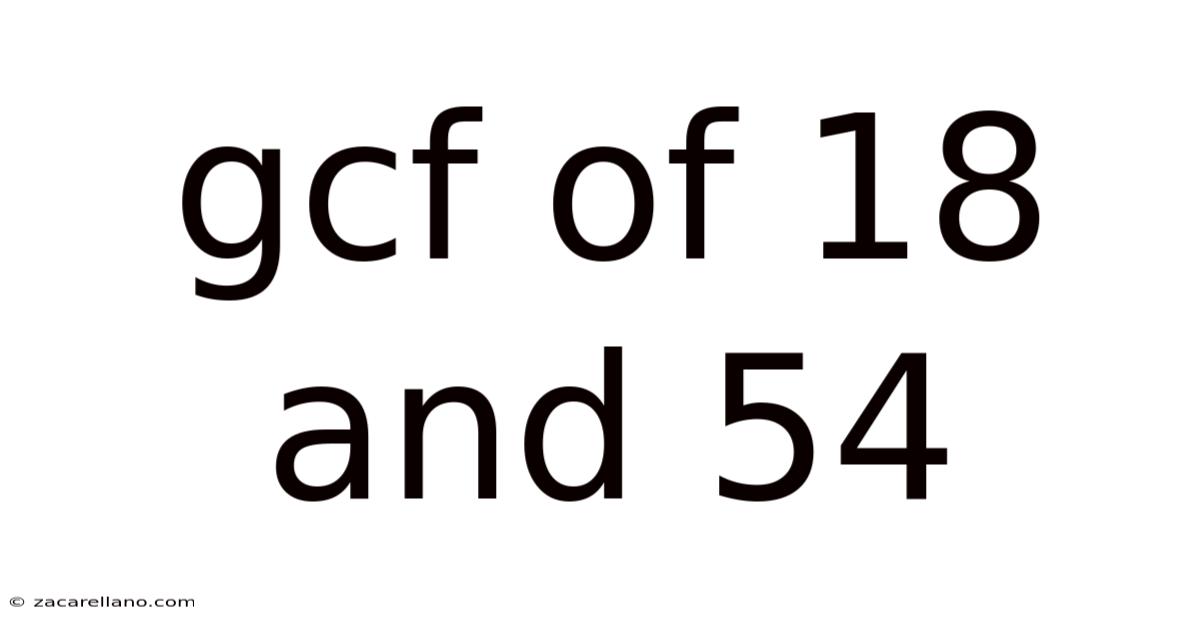
Table of Contents
Unlocking the Secrets of GCF: A Deep Dive into the Greatest Common Factor of 18 and 54
Finding the greatest common factor (GCF) might seem like a simple arithmetic task, but understanding the underlying principles unlocks a powerful tool for simplifying fractions, solving algebraic equations, and even appreciating the elegance of number theory. This comprehensive guide will explore the GCF of 18 and 54, demonstrating various methods to calculate it and highlighting its significance in mathematics. We'll delve beyond the simple answer, exploring the conceptual basis and practical applications of finding the greatest common factor.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For instance, if we consider the numbers 12 and 18, the common factors are 1, 2, 3, and 6. The greatest of these common factors is 6; therefore, the GCF of 12 and 18 is 6.
Methods for Finding the GCF of 18 and 54
Several methods can be employed to determine the GCF of 18 and 54. Let's explore three common approaches:
1. Listing Factors:
This method involves listing all the factors of each number and identifying the largest common factor.
- Factors of 18: 1, 2, 3, 6, 9, 18
- Factors of 54: 1, 2, 3, 6, 9, 18, 27, 54
By comparing the lists, we see that the common factors are 1, 2, 3, 6, 9, and 18. The greatest of these is 18. Therefore, the GCF(18, 54) = 18.
This method works well for smaller numbers but can become cumbersome with larger numbers.
2. Prime Factorization:
This method utilizes the prime factorization of each number. The prime factorization of a number is the expression of that number as a product of prime numbers.
- Prime factorization of 18: 2 x 3 x 3 = 2 x 3²
- Prime factorization of 54: 2 x 3 x 3 x 3 = 2 x 3³
To find the GCF using prime factorization, we identify the common prime factors and their lowest powers. Both 18 and 54 share a factor of 2 and three factors of 3. The lowest power of 2 is 2¹ and the lowest power of 3 is 3². Therefore:
GCF(18, 54) = 2¹ x 3² = 2 x 9 = 18
3. Euclidean Algorithm:
The Euclidean algorithm is a highly efficient method for finding the GCF, especially for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCF.
Let's apply the Euclidean algorithm to 18 and 54:
- Divide the larger number (54) by the smaller number (18): 54 ÷ 18 = 3 with a remainder of 0.
Since the remainder is 0, the GCF is the divisor, which is 18. Therefore, GCF(18, 54) = 18.
Why is the GCF Important?
Understanding and calculating the GCF is crucial for several mathematical operations and concepts:
-
Simplifying Fractions: The GCF is essential for simplifying fractions to their lowest terms. For example, the fraction 54/18 can be simplified by dividing both the numerator and the denominator by their GCF (18): 54/18 = (54÷18) / (18÷18) = 3/1 = 3.
-
Solving Equations: The GCF plays a role in solving certain types of algebraic equations, particularly those involving factoring.
-
Number Theory: The concept of GCF is fundamental in number theory, a branch of mathematics that deals with the properties of integers. It forms the basis for other concepts like least common multiple (LCM) and modular arithmetic.
-
Real-World Applications: While not directly obvious, GCF finds applications in various real-world scenarios. For example, imagine you have 18 red marbles and 54 blue marbles. You want to divide them into identical bags, with each bag containing the same number of red and blue marbles. The GCF (18) tells you that you can create 18 identical bags, each containing 1 red marble and 3 blue marbles (54/18 = 3).
Beyond the Basics: Exploring LCM and the Relationship Between GCF and LCM
The least common multiple (LCM) is another important concept related to the GCF. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers. There's a fascinating relationship between the GCF and the LCM of two numbers (a and b):
GCF(a, b) x LCM(a, b) = a x b
For our example, GCF(18, 54) = 18. Using the formula above, we can find the LCM(18, 54):
18 x LCM(18, 54) = 18 x 54 LCM(18, 54) = (18 x 54) / 18 = 54
This relationship provides a shortcut for calculating the LCM if the GCF is already known.
Frequently Asked Questions (FAQ)
-
Q: Is the GCF always smaller than the numbers involved?
- A: Yes, the GCF is always less than or equal to the smallest of the numbers involved. It cannot be larger.
-
Q: What is the GCF of two prime numbers?
- A: The GCF of two prime numbers is always 1, since prime numbers only have 1 and themselves as factors.
-
Q: Can the GCF be 1?
- A: Yes, if the two numbers are relatively prime (meaning they have no common factors other than 1), their GCF is 1.
-
Q: Is there a limit to how many methods can be used to find the GCF?
- A: No, there are several different algorithms and approaches to find the GCF. The best method depends on the numbers involved and the context of the problem.
Conclusion
Finding the greatest common factor of 18 and 54, which is 18, might seem like a straightforward calculation. However, exploring different methods – listing factors, prime factorization, and the Euclidean algorithm – reveals the depth and elegance of this fundamental mathematical concept. Understanding the GCF extends far beyond simple arithmetic; it's a cornerstone of number theory and a crucial tool for simplifying fractions, solving equations, and even tackling real-world problems. By mastering the concept of GCF and its relationship with LCM, you gain a powerful skillset that will enhance your understanding and appreciation of mathematics.
Latest Posts
Latest Posts
-
Federal Bureaucracy Definition Ap Gov
Sep 18, 2025
-
The Call Of St Matthew
Sep 18, 2025
-
Even Number Times Odd Number
Sep 18, 2025
-
Action And Reaction Force Pairs
Sep 18, 2025
-
Limiting Reagent Problems With Answers
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 18 And 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.