Gcf Of 20 And 10
zacarellano
Sep 07, 2025 · 6 min read
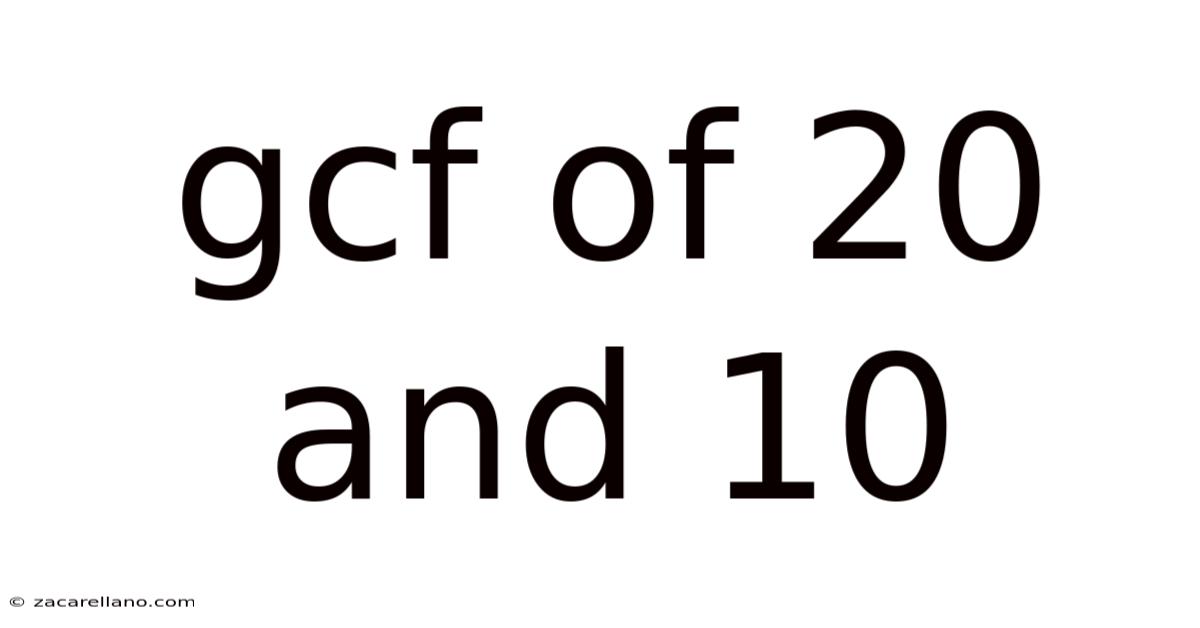
Table of Contents
Finding the Greatest Common Factor (GCF) of 20 and 10: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. It forms the basis for simplifying fractions, solving algebraic equations, and understanding number theory. This article will provide a comprehensive understanding of how to find the GCF of 20 and 10, exploring different methods and delving into the underlying mathematical principles. We'll move beyond simply stating the answer and delve into the "why" behind the calculations, making this concept accessible to everyone from elementary school students to those brushing up on their math skills.
Understanding the Greatest Common Factor (GCF)
The GCF of two or more numbers is the largest number that divides evenly into all of the numbers. In simpler terms, it's the biggest number that is a factor of all the given numbers. For example, the factors of 10 are 1, 2, 5, and 10. The factors of 20 are 1, 2, 4, 5, 10, and 20. The greatest number that appears in both lists is 10. Therefore, the GCF of 10 and 20 is 10.
Method 1: Listing Factors
This is the most straightforward method, particularly suitable for smaller numbers like 20 and 10.
-
List the factors of each number:
- Factors of 10: 1, 2, 5, 10
- Factors of 20: 1, 2, 4, 5, 10, 20
-
Identify common factors: Look for the numbers that appear in both lists. In this case, the common factors are 1, 2, 5, and 10.
-
Determine the greatest common factor: The largest number among the common factors is 10. Therefore, the GCF of 20 and 10 is 10.
This method is intuitive and easy to visualize, making it a great starting point for understanding the concept of GCF. However, it becomes less efficient when dealing with larger numbers.
Method 2: Prime Factorization
Prime factorization involves expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...). This method is more systematic and works well even with larger numbers.
-
Find the prime factorization of each number:
- 10 = 2 × 5
- 20 = 2 × 2 × 5 = 2² × 5
-
Identify common prime factors: Look for the prime factors that appear in both factorizations. Both 10 and 20 have a 2 and a 5 as prime factors.
-
Multiply the common prime factors: Multiply the common prime factors together to find the GCF. In this case, we have 2 × 5 = 10. Therefore, the GCF of 20 and 10 is 10.
This method is particularly useful for understanding the structure of numbers and provides a solid foundation for more advanced mathematical concepts.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially large ones. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
-
Start with the two numbers: We have 20 and 10.
-
Repeatedly subtract the smaller number from the larger number:
- 20 - 10 = 10
- Now we have 10 and 10.
-
The GCF is the remaining number: Since both numbers are now 10, the GCF of 20 and 10 is 10.
Alternatively, a more efficient version of the Euclidean algorithm uses division with remainder.
-
Divide the larger number by the smaller number and find the remainder:
- 20 ÷ 10 = 2 with a remainder of 0
-
If the remainder is 0, the smaller number is the GCF: Since the remainder is 0, the GCF is 10.
If the remainder were not 0, we would replace the larger number with the smaller number and the smaller number with the remainder, and repeat the division process until we get a remainder of 0. This method is significantly more efficient for larger numbers.
Why is the GCF Important?
Understanding the GCF has practical applications in various areas:
-
Simplifying Fractions: The GCF helps simplify fractions to their lowest terms. For example, the fraction 20/10 can be simplified by dividing both the numerator and denominator by their GCF (10), resulting in the simplified fraction 2/1 or simply 2.
-
Algebra: GCF is used in factoring algebraic expressions. Finding the GCF of the terms in an expression allows for simplification and solving equations.
-
Geometry: GCF is relevant in geometry problems involving finding the greatest common dimensions of shapes.
-
Number Theory: GCF is a fundamental concept in number theory, forming the basis for understanding more complex number relationships.
Extending the Concept: GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For the listing factors method, you would list the factors of all numbers and find the largest common factor among them. For prime factorization, you would find the prime factorization of each number and identify the common prime factors, multiplying them to obtain the GCF. For the Euclidean algorithm, you would apply it iteratively, finding the GCF of two numbers at a time, and then finding the GCF of that result and the next number, and so on.
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they share no common factors other than 1.
Q: Is there a limit to the size of numbers for which I can find the GCF?
A: While the listing factors method becomes impractical for very large numbers, the prime factorization and Euclidean algorithm methods can be applied to numbers of virtually any size, although computational time may increase.
Q: Can I use a calculator to find the GCF?
A: Many calculators, particularly scientific calculators, have built-in functions to calculate the GCF of two or more numbers. You can also find online GCF calculators.
Conclusion
Finding the GCF of 20 and 10, as demonstrated through various methods, is more than just a simple arithmetic exercise. It provides a foundation for understanding fundamental concepts in mathematics, including number theory, algebra, and fraction simplification. By mastering these techniques, you'll not only be able to find the GCF efficiently but also appreciate the underlying mathematical principles that govern this important concept. The ability to find the GCF extends beyond simple calculations; it's a crucial skill that unlocks deeper understanding in various mathematical applications. Remember, practice is key to mastering this concept. Try applying these methods to different pairs of numbers to reinforce your learning and build confidence.
Latest Posts
Latest Posts
-
Abbasid Caliphate Ap World History
Sep 08, 2025
-
Whats The Antiderivative Of X
Sep 08, 2025
-
Definite Article Vs Indefinite Article
Sep 08, 2025
-
Is Oxygen Required For Glycolysis
Sep 08, 2025
-
Integrate By Completing The Square
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 20 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.