Gcf Of 20 And 40
zacarellano
Sep 21, 2025 · 6 min read
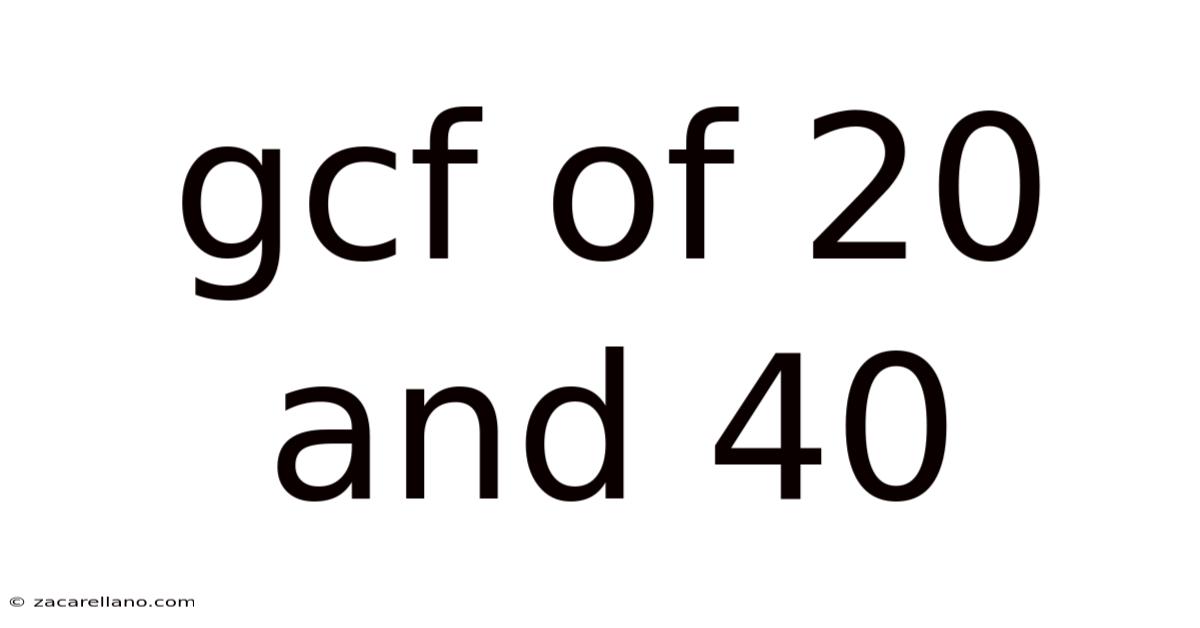
Table of Contents
Understanding the Greatest Common Factor (GCF) of 20 and 40
Finding the Greatest Common Factor (GCF), also known as the Greatest Common Divisor (GCD), is a fundamental concept in mathematics with applications spanning various fields, from simplifying fractions to solving complex algebraic equations. This article delves deep into understanding the GCF, specifically focusing on how to calculate the GCF of 20 and 40, exploring different methods, and highlighting the broader significance of this mathematical operation. We'll go beyond a simple answer and explore the underlying principles and applications.
What is the Greatest Common Factor (GCF)?
The Greatest Common Factor (GCF) of two or more numbers is the largest number that divides evenly into all of them without leaving a remainder. In simpler terms, it's the biggest number that is a factor of all the given numbers. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6; therefore, the GCF of 12 and 18 is 6.
Calculating the GCF of 20 and 40: Multiple Methods
There are several effective methods to determine the GCF of 20 and 40. Let's explore the most common approaches:
1. Listing Factors Method:
This method involves listing all the factors of each number and then identifying the largest common factor.
- Factors of 20: 1, 2, 4, 5, 10, 20
- Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
Comparing the two lists, we can see that the common factors are 1, 2, 4, 5, 10, and 20. The greatest among these is 20. Therefore, the GCF of 20 and 40 is 20.
This method is straightforward for smaller numbers, but it can become cumbersome and time-consuming when dealing with larger numbers or multiple numbers.
2. Prime Factorization Method:
This is a more efficient method, especially for larger numbers. It involves finding the prime factorization of each number and then identifying the common prime factors raised to the lowest power.
- Prime Factorization of 20: 2² x 5
- Prime Factorization of 40: 2³ x 5
The common prime factors are 2 and 5. The lowest power of 2 is 2² (which is 4), and the lowest power of 5 is 5¹. Multiplying these together: 2² x 5 = 20. Therefore, the GCF of 20 and 40 is 20.
This method is more systematic and less prone to error, especially when dealing with larger numbers.
3. Euclidean Algorithm:
The Euclidean Algorithm is a highly efficient method for finding the GCF of two numbers, especially large ones. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Let's apply the Euclidean Algorithm to 20 and 40:
- Start with the larger number (40) and the smaller number (20).
- Divide the larger number by the smaller number: 40 ÷ 20 = 2 with a remainder of 0.
- Since the remainder is 0, the GCF is the smaller number, which is 20.
The Euclidean Algorithm is particularly useful for finding the GCF of very large numbers because it significantly reduces the computational effort compared to other methods.
Understanding the Concept of Divisibility
The concept of divisibility is crucial to understanding GCF. A number is divisible by another number if it can be divided by that number without leaving a remainder. For example, 20 is divisible by 2, 4, 5, and 10 because these numbers divide evenly into 20. This understanding helps in identifying factors and ultimately, the GCF. The divisibility rules for specific numbers (like 2, 3, 5, 10) can speed up the process of finding factors.
Applications of the Greatest Common Factor
The GCF has numerous applications across various branches of mathematics and beyond:
-
Simplifying Fractions: The GCF is essential for reducing fractions to their simplest form. For example, the fraction 40/20 can be simplified by dividing both the numerator and denominator by their GCF (20), resulting in the simplified fraction 2/1 or simply 2.
-
Solving Algebraic Equations: GCF plays a role in factoring algebraic expressions, which is crucial in solving various types of equations.
-
Geometry and Measurement: GCF helps in solving problems related to area, volume, and other geometric calculations. For example, finding the largest square tile that can perfectly cover a rectangular floor requires calculating the GCF of the length and width of the floor.
-
Number Theory: The GCF is a fundamental concept in number theory, contributing to the understanding of prime numbers, divisibility, and other related properties.
-
Computer Science: Algorithms for finding the GCF are used in various computer science applications, including cryptography and data compression.
Beyond the Basics: GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For the listing factors method, you would simply list the factors of all the numbers and find the largest common factor. For the prime factorization method, you would find the prime factorization of each number and then identify the common prime factors raised to the lowest power, multiplying them together to find the GCF. The Euclidean Algorithm can be extended iteratively.
Frequently Asked Questions (FAQ)
Q: Is the GCF always smaller than the numbers involved?
A: No, the GCF can be equal to one of the numbers, as seen in our example where the GCF of 20 and 40 is 20. This happens when one number is a multiple of the other.
Q: What is the GCF of two prime numbers?
A: The GCF of two distinct prime numbers is always 1. Prime numbers only have themselves and 1 as factors.
Q: Can the GCF of two numbers be 0?
A: No, the GCF cannot be 0. The GCF represents a common divisor, and 0 cannot be a divisor.
Q: What if I have a set of numbers with no common factors other than 1?
A: If the only common factor of a set of numbers is 1, then their GCF is 1.
Conclusion: Mastering the GCF
Understanding the Greatest Common Factor is a critical skill in mathematics. By mastering the different methods for calculating the GCF – the listing factors method, prime factorization, and the Euclidean Algorithm – you equip yourself with valuable tools applicable to various mathematical concepts and problem-solving situations. The GCF is not just a simple mathematical operation; it is a fundamental building block for more advanced mathematical concepts, and its understanding opens doors to deeper comprehension of number theory and its applications in various fields. Remember that practicing different methods with various numbers will solidify your understanding and build confidence in your ability to tackle more complex mathematical problems. The journey to mathematical proficiency is a process of consistent learning and application; embrace the challenge and enjoy the rewards of mastery.
Latest Posts
Latest Posts
-
Pa Art History Practice Test
Sep 21, 2025
-
Zero Pair Definition In Math
Sep 21, 2025
-
Did Hindu Gods Really Exist
Sep 21, 2025
-
6th Grade Decimal Word Problems
Sep 21, 2025
-
Standard Form Vs General Form
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 20 And 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.