Gcf Of 24 And 28
zacarellano
Sep 13, 2025 · 6 min read
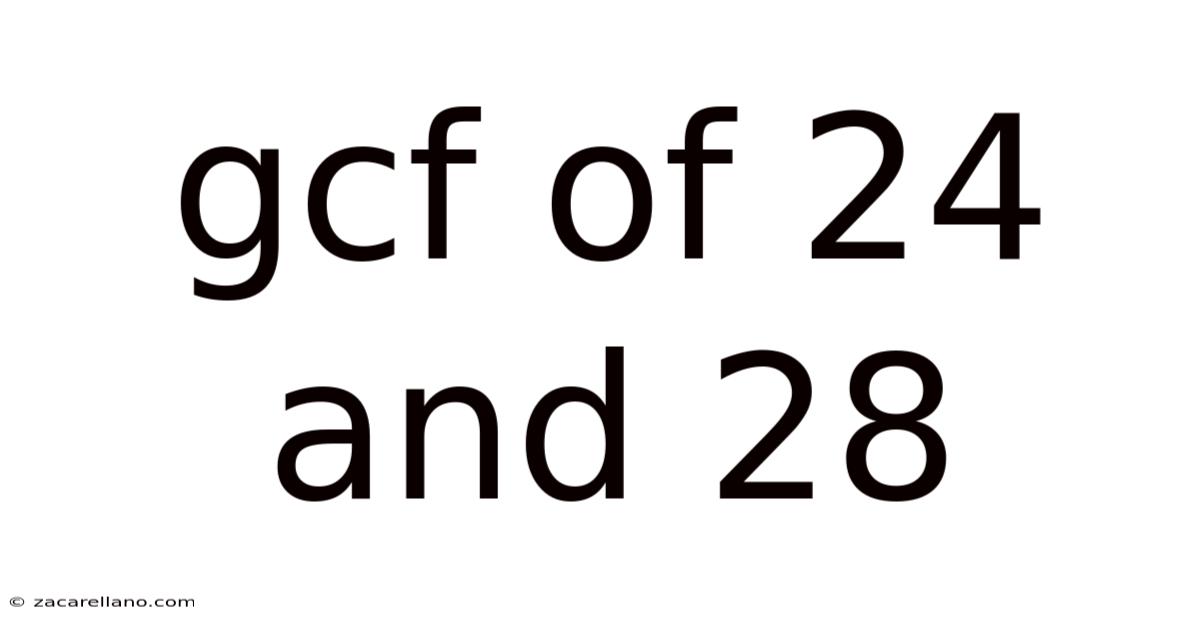
Table of Contents
Finding the Greatest Common Factor (GCF) of 24 and 28: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics with applications across various fields, from simplifying fractions to solving algebraic equations. This article will delve deep into the methods for determining the GCF of 24 and 28, explaining the process step-by-step, exploring different techniques, and providing a solid foundation for understanding this important mathematical concept. We'll also touch upon the theoretical underpinnings and explore some real-world applications.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more numbers is the largest number that divides each of the numbers without leaving a remainder. In simpler terms, it's the biggest number that's a factor of both numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The greatest common factor of 12 and 18 is 6, as it's the largest number that divides both 12 and 18 evenly.
Method 1: Listing Factors
The most straightforward method for finding the GCF of relatively small numbers like 24 and 28 is by listing their factors.
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Factors of 28: 1, 2, 4, 7, 14, 28
By comparing the two lists, we can identify the common factors: 1, 2, and 4. The largest of these common factors is 4. Therefore, the GCF of 24 and 28 is 4.
This method works well for small numbers, but it becomes cumbersome and inefficient when dealing with larger numbers.
Method 2: Prime Factorization
A more efficient and generally applicable method is prime factorization. This involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves.
Prime Factorization of 24:
24 = 2 x 12 = 2 x 2 x 6 = 2 x 2 x 2 x 3 = 2³ x 3¹
Prime Factorization of 28:
28 = 2 x 14 = 2 x 2 x 7 = 2² x 7¹
Once we have the prime factorizations, we identify the common prime factors and their lowest powers. Both 24 and 28 share a common prime factor of 2. The lowest power of 2 present in both factorizations is 2².
Therefore, the GCF is 2² = 4.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers where listing factors or prime factorization becomes tedious. This algorithm is based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Let's apply the Euclidean algorithm to 24 and 28:
- Step 1: Subtract the smaller number (24) from the larger number (28): 28 - 24 = 4
- Step 2: Now we find the GCF of 24 and 4. We repeat the process: 24 - 4(6) = 0
- Since the remainder is 0, the GCF is the last non-zero remainder, which is 4.
This algorithm is remarkably efficient and avoids the need for extensive factor listing or prime factorization, making it suitable for larger numbers.
Mathematical Explanation: Why these methods work
The methods outlined above all rely on fundamental properties of numbers and their factors. The prime factorization method leverages the Fundamental Theorem of Arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers. By finding the common prime factors and their lowest powers, we essentially identify the largest number that divides both original numbers without leaving a remainder.
The Euclidean algorithm's effectiveness stems from the property that the GCF of two numbers remains unchanged when the larger number is replaced by its difference with the smaller number. This iterative process efficiently reduces the problem until the GCF becomes apparent.
Applications of GCF in Real-World Scenarios
The concept of GCF is not merely an abstract mathematical exercise; it has practical applications in various fields:
-
Simplifying Fractions: Finding the GCF of the numerator and denominator allows us to simplify fractions to their lowest terms. For example, the fraction 24/28 can be simplified to 6/7 by dividing both numerator and denominator by their GCF, which is 4.
-
Measurement and Division: When dealing with measurements, finding the GCF can help determine the largest common unit for measuring. For instance, if you have two pieces of wood, one 24 inches long and the other 28 inches long, the GCF (4 inches) tells you the longest length you can cut both pieces into without any remainder.
-
Algebra and Number Theory: GCF plays a crucial role in solving Diophantine equations (equations where solutions must be integers) and other problems in number theory.
-
Computer Science: Algorithms for finding the GCF, like the Euclidean algorithm, are fundamental in computer science for tasks involving cryptography and data processing.
Frequently Asked Questions (FAQ)
-
Q: What if the GCF of two numbers is 1?
- A: If the GCF of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they share no common factors other than 1.
-
Q: Can I use these methods for more than two numbers?
- A: Yes! For more than two numbers, you can extend the prime factorization method by finding the common prime factors among all numbers and their lowest powers. For the Euclidean algorithm, you can iteratively find the GCF of pairs of numbers.
-
Q: Is there a formula for calculating the GCF?
- A: There isn't a single, direct formula for calculating the GCF, but the methods described (prime factorization and the Euclidean algorithm) provide systematic procedures to find it.
-
Q: Why is the Euclidean algorithm so efficient?
- A: The Euclidean algorithm's efficiency stems from its iterative nature, which rapidly reduces the size of the numbers involved. It avoids the potentially lengthy process of completely factoring the numbers, making it much faster for large numbers.
Conclusion
Finding the greatest common factor of two numbers, such as 24 and 28, is a fundamental skill with broad applications across mathematics and other disciplines. This article has explored three primary methods: listing factors, prime factorization, and the Euclidean algorithm. Understanding these methods not only allows for the calculation of the GCF but also provides insight into the underlying mathematical principles. Mastering these techniques provides a robust foundation for tackling more complex mathematical problems and real-world applications where the concept of GCF proves invaluable. Remember, choosing the most appropriate method often depends on the size of the numbers involved; for smaller numbers, listing factors may suffice, while for larger numbers, the efficiency of the Euclidean algorithm shines. The understanding gained from exploring these methods will undoubtedly enhance your mathematical comprehension and problem-solving skills.
Latest Posts
Latest Posts
-
Formula Del Area De Rectangulo
Sep 13, 2025
-
Find Normal Vector Of Plane
Sep 13, 2025
-
Light Work No Reaction Meaning
Sep 13, 2025
-
1 3 Minus 1 4
Sep 13, 2025
-
Math Quiz For 7th Graders
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 24 And 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.