Gcf Of 25 And 40
zacarellano
Sep 14, 2025 · 6 min read
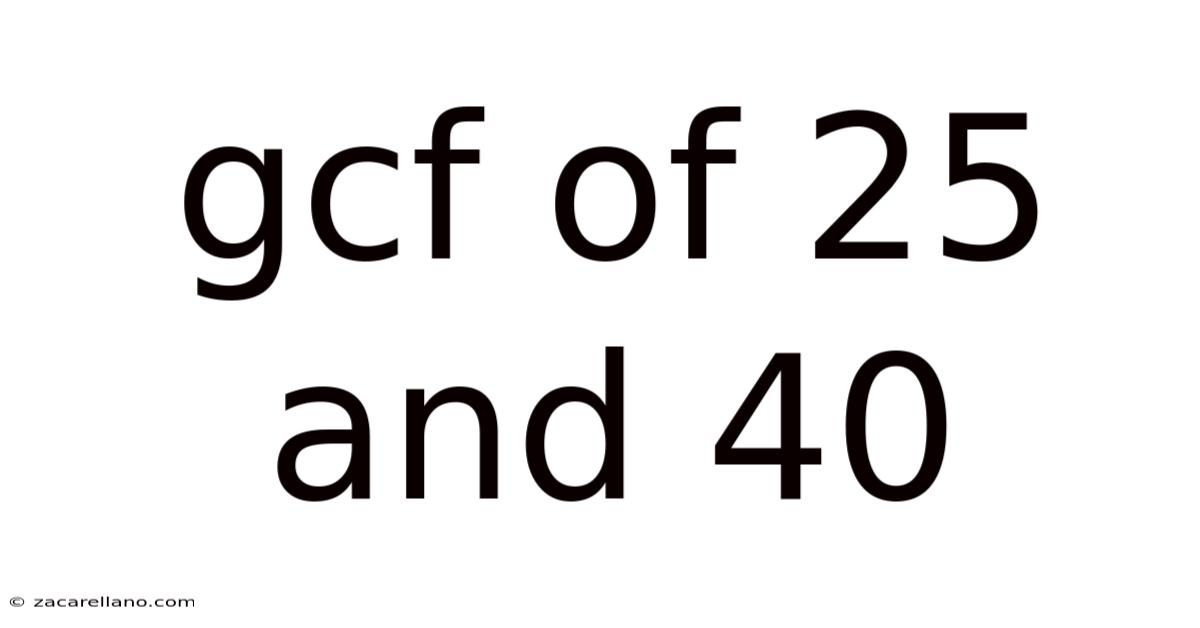
Table of Contents
Finding the Greatest Common Factor (GCF) of 25 and 40: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics with applications ranging from simplifying fractions to solving algebraic equations. This article provides a thorough exploration of how to determine the GCF of 25 and 40, using various methods, explaining the underlying principles, and addressing common questions. Understanding GCF is crucial for a strong foundation in arithmetic and algebra.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more numbers is the largest number that divides evenly into all of them without leaving a remainder. In simpler terms, it's the biggest number that is a factor of all the given numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6, so the GCF of 12 and 18 is 6.
This concept is essential for simplifying fractions, understanding ratios, and solving various mathematical problems. We'll now delve into several methods to find the GCF of 25 and 40.
Method 1: Listing Factors
The most straightforward method, especially for smaller numbers, is to list all the factors of each number and identify the largest common factor.
Factors of 25: 1, 5, 25
Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
Comparing the two lists, we see that the common factors are 1 and 5. The greatest of these common factors is 5.
Therefore, the GCF of 25 and 40 is 5.
Method 2: Prime Factorization
This method is more efficient for larger numbers. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves.
Prime Factorization of 25:
25 = 5 x 5 = 5²
Prime Factorization of 40:
40 = 2 x 2 x 2 x 5 = 2³ x 5
Now, we identify the common prime factors and their lowest powers. Both 25 and 40 share one factor of 5 (5¹). There are no other common prime factors.
Therefore, the GCF of 25 and 40 is 5.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Let's apply the Euclidean algorithm to 25 and 40:
- Step 1: Subtract the smaller number (25) from the larger number (40): 40 - 25 = 15
- Step 2: Now we find the GCF of 25 and 15. Subtract the smaller number (15) from the larger number (25): 25 - 15 = 10
- Step 3: Find the GCF of 15 and 10. Subtract the smaller number (10) from the larger number (15): 15 - 10 = 5
- Step 4: Find the GCF of 10 and 5. Subtract the smaller number (5) from the larger number (10): 10 - 5 = 5
- Step 5: The numbers are now equal (5 and 5). Therefore, the GCF is 5.
Visual Representation using Venn Diagrams
Venn diagrams can help visualize the concept of common factors. Let's represent the factors of 25 and 40 in a Venn diagram:
- Circle 1 (Factors of 25): 1, 5, 25
- Circle 2 (Factors of 40): 1, 2, 4, 5, 8, 10, 20, 40
The overlapping section of the two circles represents the common factors. In this case, the overlapping section contains 1 and 5. The largest number in the overlapping section is 5, which confirms that the GCF is 5.
Applications of GCF
Understanding and calculating the GCF has numerous applications in various areas of mathematics and beyond:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 20/40 can be simplified by dividing both the numerator and denominator by their GCF, which is 20. This simplifies to 1/2.
-
Solving Algebraic Equations: GCF plays a vital role in factoring algebraic expressions, a key step in solving many algebraic equations.
-
Ratio and Proportion: GCF helps in simplifying ratios to their simplest form. For instance, a ratio of 25:40 can be simplified to 5:8 by dividing both parts by the GCF (5).
-
Real-World Applications: GCF can be used in practical scenarios like dividing items evenly into groups or determining the size of the largest square tile that can perfectly cover a rectangular area.
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, it means they are relatively prime or coprime. This indicates that they share no common factors other than 1.
Q: Can the GCF of two numbers be negative?
A: While we typically consider only positive factors, the GCF could be considered negative if we include negative factors. However, convention focuses on the positive GCF.
Q: Is there a limit to the size of numbers for which we can find the GCF?
A: No, the methods described above, especially the Euclidean algorithm, can be applied to numbers of any size, although the calculations might become more complex for extremely large numbers. Computer algorithms are frequently used for such calculations.
Q: What is the difference between LCM and GCF?
A: The least common multiple (LCM) is the smallest number that is a multiple of both numbers, while the GCF is the largest number that is a factor of both numbers. They are inversely related; the product of the LCM and GCF of two numbers is equal to the product of the two numbers.
Conclusion
Finding the greatest common factor (GCF) is a foundational skill in mathematics. We've explored several methods – listing factors, prime factorization, and the Euclidean algorithm – to effectively determine the GCF of 25 and 40, which is 5. Understanding these methods empowers you to tackle more complex mathematical problems and appreciate the underlying principles of number theory. The ability to efficiently calculate the GCF is not only beneficial for academic success but also enhances problem-solving skills applicable to various real-world scenarios. Remember to choose the method best suited to the numbers involved; for smaller numbers, listing factors might suffice, while the Euclidean algorithm proves more efficient for larger numbers. Mastering the GCF concept builds a strong base for more advanced mathematical concepts.
Latest Posts
Latest Posts
-
Macro And Micro In Sociology
Sep 14, 2025
-
Finding The Centre Of Rotation
Sep 14, 2025
-
What Is Mgh In Physics
Sep 14, 2025
-
Famous Landmarks In Georgia Usa
Sep 14, 2025
-
Greatest Common Factor Of 21
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 25 And 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.