Gcf Of 27 And 72
zacarellano
Sep 19, 2025 · 6 min read
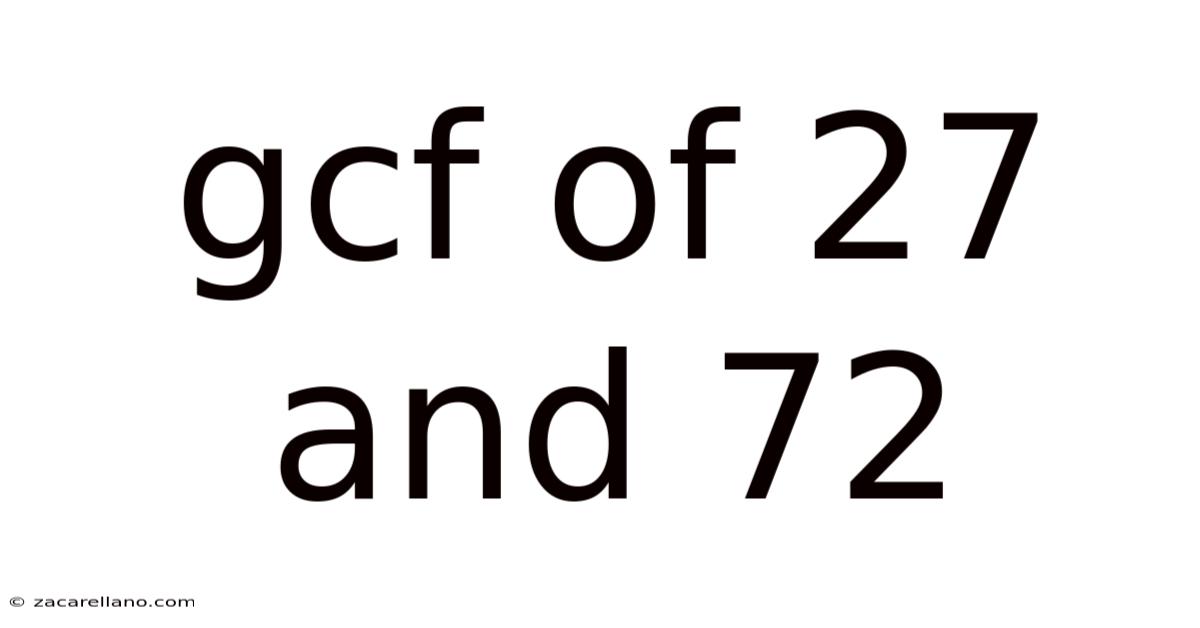
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 27 and 72: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics with wide-ranging applications, from simplifying fractions to solving algebraic equations. This comprehensive guide will explore various methods for determining the GCF of 27 and 72, delving into the underlying principles and providing a solid foundation for understanding this crucial mathematical concept. We'll move beyond simply finding the answer and explore why this process is important and how it applies to more complex mathematical situations.
Introduction: Understanding the Greatest Common Factor
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that can perfectly divide both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 evenly. Understanding the GCF is crucial for simplifying fractions, solving problems involving ratios and proportions, and even in more advanced areas of mathematics like abstract algebra. This article will focus on finding the GCF of 27 and 72 using several methods, explaining each step clearly and comprehensively.
Method 1: Listing Factors
This is the most straightforward method, especially for smaller numbers. We start by listing all the factors of each number:
- Factors of 27: 1, 3, 9, 27
- Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Now, we identify the common factors – the numbers that appear in both lists: 1, 3, and 9. The greatest of these common factors is 9. Therefore, the GCF of 27 and 72 is 9.
This method is simple and intuitive, but it becomes less efficient as the numbers get larger. Finding all the factors of a large number can be time-consuming.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical structure. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
- Prime factorization of 27: 3 x 3 x 3 = 3³
- Prime factorization of 72: 2 x 2 x 2 x 3 x 3 = 2³ x 3²
To find the GCF, we identify the common prime factors and take the lowest power of each. Both numbers have 3 as a prime factor. The lowest power of 3 present in both factorizations is 3². Therefore, the GCF is 3² = 9.
This method is more systematic and efficient than listing factors, especially for larger numbers. It provides a clearer understanding of the number's composition and its relationship with other numbers.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Let's apply the Euclidean algorithm to find the GCF of 27 and 72:
- Divide the larger number (72) by the smaller number (27): 72 ÷ 27 = 2 with a remainder of 18.
- Replace the larger number (72) with the remainder (18): Now we find the GCF of 27 and 18.
- Divide the larger number (27) by the smaller number (18): 27 ÷ 18 = 1 with a remainder of 9.
- Replace the larger number (27) with the remainder (9): Now we find the GCF of 18 and 9.
- Divide the larger number (18) by the smaller number (9): 18 ÷ 9 = 2 with a remainder of 0.
Since the remainder is 0, the GCF is the last non-zero remainder, which is 9.
The Euclidean algorithm is an elegant and efficient method, especially suitable for computer programming due to its iterative nature. It's significantly faster than listing factors or prime factorization for very large numbers.
Explanation of the Mathematical Principles Involved
The GCF calculation is fundamentally based on the concept of divisibility. A number a is divisible by another number b if there exists an integer k such that a = bk. The GCF represents the largest integer that satisfies this condition for both numbers involved. The prime factorization method highlights the fundamental building blocks of numbers, revealing the common factors in a structured way. The Euclidean algorithm leverages the properties of divisibility to efficiently arrive at the GCF without needing to find all the factors.
Applications of GCF in Real-World Scenarios
The GCF finds applications in various real-world scenarios:
- Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 72/27 can be simplified to 8/3 by dividing both the numerator and denominator by their GCF, which is 9.
- Ratio and Proportion Problems: The GCF helps in simplifying ratios and proportions to their simplest forms, making them easier to understand and work with.
- Measurement and Geometry: The GCF is used to determine the largest possible square tile that can be used to cover a rectangular floor without any gaps or overlaps.
- Number Theory and Cryptography: The GCF plays a crucial role in number theory and advanced applications like cryptography.
Frequently Asked Questions (FAQ)
-
Q: What if the GCF of two numbers is 1? A: If the GCF of two numbers is 1, they are called relatively prime or coprime. This means they have no common factors other than 1.
-
Q: Can I use a calculator to find the GCF? A: Yes, many calculators have built-in functions or programs to calculate the GCF. Some online calculators are also readily available.
-
Q: How do I find the GCF of more than two numbers? A: You can extend the methods discussed above to find the GCF of multiple numbers. For example, using prime factorization, you would find the prime factorization of each number and select the common prime factors raised to their lowest powers. The Euclidean algorithm can also be extended to handle more than two numbers, though it becomes slightly more complex.
-
Q: What is the difference between GCF and LCM? A: The GCF is the greatest common factor, while the LCM is the least common multiple. The LCM is the smallest number that is a multiple of both given numbers. For example, the LCM of 27 and 72 is 216. The product of the GCF and LCM of two numbers is always equal to the product of the two numbers. In our case, 9 (GCF) * 216 (LCM) = 1944, and 27 * 72 = 1944.
Conclusion:
Finding the greatest common factor is a fundamental skill in mathematics with far-reaching applications. This guide has explored various methods for determining the GCF of 27 and 72, highlighting their strengths and weaknesses. Whether you choose to list factors, use prime factorization, or employ the efficient Euclidean algorithm, understanding the underlying principles of divisibility and prime numbers will empower you to solve GCF problems effectively. Remember that the chosen method often depends on the size of the numbers involved and the available tools. The ability to confidently calculate the GCF is a cornerstone of mathematical fluency and problem-solving abilities.
Latest Posts
Latest Posts
-
Examples Of Mutations In Animals
Sep 20, 2025
-
Seven Years War Apush Definition
Sep 20, 2025
-
Eley Rideal Mechanism Or Ter Mechnisam
Sep 20, 2025
-
Life Supporting Properties Of Water
Sep 20, 2025
-
Gene Drift Vs Gene Flow
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 27 And 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.