Gcf Of 30 And 18
zacarellano
Sep 20, 2025 · 5 min read
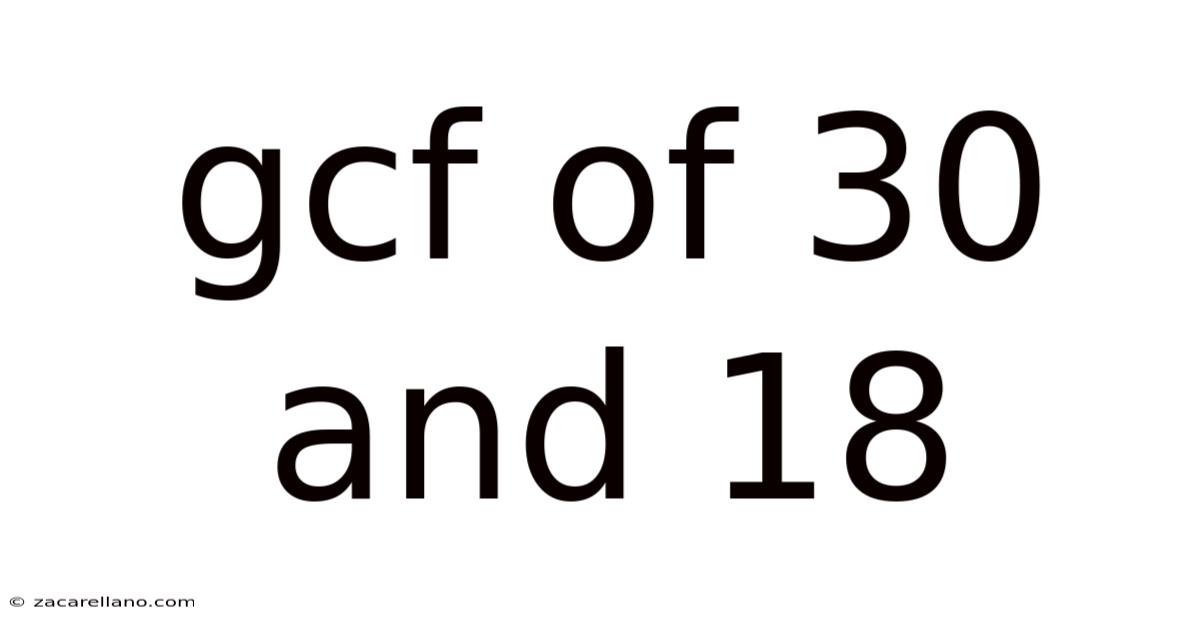
Table of Contents
Finding the Greatest Common Factor (GCF) of 30 and 18: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics with applications spanning various fields, from simplifying fractions to solving algebraic equations. This article provides a thorough explanation of how to find the GCF of 30 and 18, exploring different methods and delving into the underlying mathematical principles. We'll also address frequently asked questions and explore the significance of GCF in broader mathematical contexts.
Understanding the Concept of GCF
Before we dive into calculating the GCF of 30 and 18, let's clarify what it means. The greatest common factor of two or more numbers is the largest number that divides each of them without leaving a remainder. In simpler terms, it's the biggest number that's a factor of both numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The greatest common factor of 12 and 18 is 6.
Method 1: Listing Factors
One straightforward method to find the GCF is by listing all the factors of each number and identifying the largest common factor. Let's apply this to 30 and 18:
- Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
- Factors of 18: 1, 2, 3, 6, 9, 18
Comparing the lists, we see that the common factors are 1, 2, 3, and 6. The greatest among these is 6. Therefore, the GCF of 30 and 18 is 6.
This method is simple for smaller numbers, but it becomes less efficient as the numbers get larger. Finding all factors of a large number can be time-consuming.
Method 2: Prime Factorization
A more efficient and systematic method, especially for larger numbers, is prime factorization. This involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
- Prime factorization of 30: 2 x 3 x 5
- Prime factorization of 18: 2 x 3 x 3
Once we have the prime factorization, we identify the common prime factors and multiply them together to find the GCF. Both 30 and 18 share a 2 and a 3 as prime factors. Therefore:
GCF(30, 18) = 2 x 3 = 6
This method is generally faster and more reliable than listing all factors, particularly when dealing with larger numbers. It's also a crucial step in understanding other mathematical concepts, such as simplifying fractions and working with least common multiples (LCM).
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly large ones. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 30 and 18:
- Start with the larger number (30) and the smaller number (18).
- Subtract the smaller number from the larger number: 30 - 18 = 12
- Replace the larger number with the result (12) and keep the smaller number (18). Now we have 18 and 12.
- Repeat the subtraction: 18 - 12 = 6
- Replace the larger number with the result (6) and keep the smaller number (12). Now we have 12 and 6.
- Repeat the subtraction: 12 - 6 = 6
- Now both numbers are equal to 6. Therefore, the GCF of 30 and 18 is 6.
The Euclidean algorithm is remarkably efficient, especially for large numbers, because it avoids the need for complete prime factorization. It's a cornerstone algorithm in number theory and has applications in computer science and cryptography.
Visualizing GCF with Venn Diagrams
Venn diagrams provide a visual representation of the relationship between sets of numbers. We can use them to understand the GCF more intuitively. Consider two circles representing the factors of 30 and 18. The overlapping area represents the common factors.
[Imagine a Venn diagram here. One circle labeled "Factors of 30" contains 1, 2, 3, 5, 6, 10, 15, 30. The other circle labeled "Factors of 18" contains 1, 2, 3, 6, 9, 18. The overlapping section contains 1, 2, 3, 6.]
The largest number in the overlapping section – the greatest common factor – is 6.
The Significance of GCF in Mathematics
The GCF has wide-ranging applications in various mathematical areas:
-
Simplifying Fractions: To simplify a fraction to its lowest terms, we divide both the numerator and the denominator by their GCF. For example, the fraction 30/18 can be simplified to 5/3 by dividing both 30 and 18 by their GCF, which is 6.
-
Solving Equations: GCF is used in solving certain types of algebraic equations, particularly those involving factoring polynomials.
-
Number Theory: GCF is a fundamental concept in number theory, a branch of mathematics focused on the properties of integers. It's essential in understanding concepts like modular arithmetic and cryptography.
-
Geometry: GCF is used in geometric problems involving finding the largest square that can tile a rectangular region.
Frequently Asked Questions (FAQ)
-
What if the GCF is 1? If the GCF of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they have no common factors other than 1.
-
Can I use a calculator to find the GCF? Many calculators and software programs have built-in functions to calculate the GCF. However, understanding the underlying methods is crucial for comprehending the mathematical concepts involved.
-
Is there a difference between GCF and GCD? No, GCF (Greatest Common Factor) and GCD (Greatest Common Divisor) are essentially the same thing. They both refer to the largest number that divides both given numbers without leaving a remainder.
Conclusion
Finding the greatest common factor is a cornerstone skill in mathematics. We've explored three different methods – listing factors, prime factorization, and the Euclidean algorithm – to determine the GCF of 30 and 18, which is 6. Each method has its strengths and weaknesses, making it crucial to understand the principles behind them. This understanding not only allows you to efficiently calculate the GCF but also to appreciate its significance in various mathematical contexts, from simplifying fractions to solving complex equations and exploring deeper concepts within number theory. Mastering the GCF lays a solid foundation for further mathematical exploration and problem-solving.
Latest Posts
Latest Posts
-
Unit 1 U S History Test
Sep 20, 2025
-
Velocity Time Graph Negative Acceleration
Sep 20, 2025
-
Ap U S History Past Exams
Sep 20, 2025
-
Confirming Continuity Over An Interval
Sep 20, 2025
-
What Is Oxidation In Photosynthesis
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 30 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.