Gcf Of 30 And 75
zacarellano
Sep 18, 2025 · 6 min read
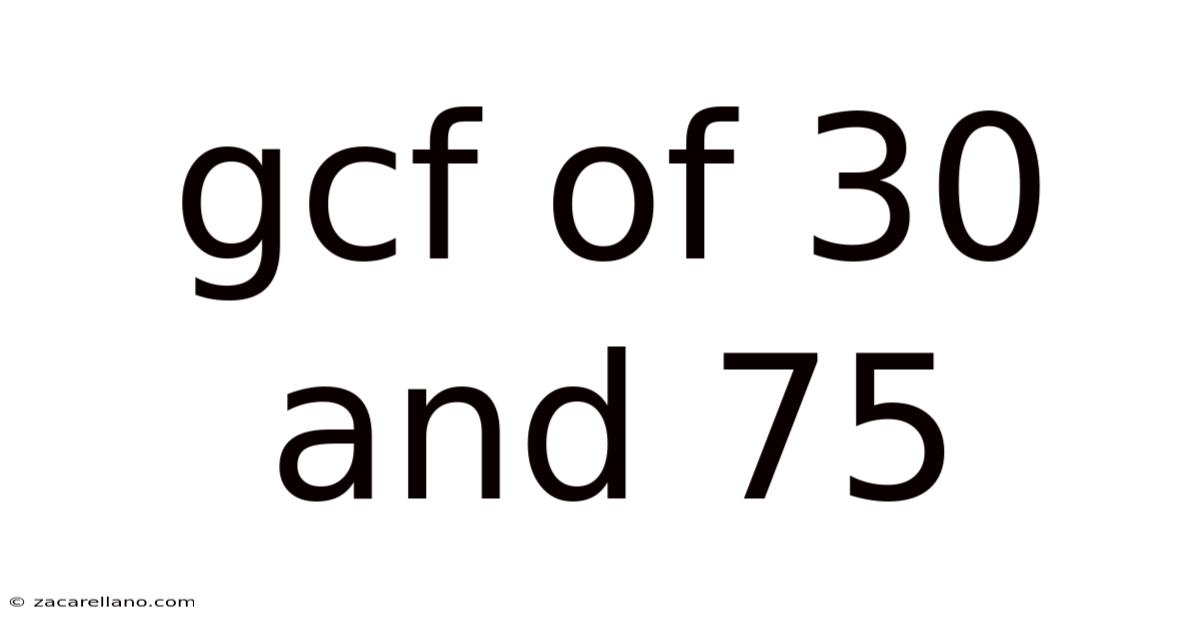
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 30 and 75: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles reveals a fascinating connection to number theory and provides valuable insights into the structure of numbers themselves. This comprehensive guide will explore the GCF of 30 and 75, demonstrating multiple methods to calculate it and explaining the mathematical concepts involved. We'll delve into prime factorization, the Euclidean algorithm, and the significance of GCF in various mathematical applications.
Understanding the Greatest Common Factor (GCF)
Before diving into the specifics of 30 and 75, let's establish a clear understanding of the GCF concept. The GCF of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. It's a fundamental concept in number theory and has practical applications in various fields, including simplifying fractions, solving algebraic equations, and even in computer science algorithms.
Think of it like finding the largest common building block of two numbers. For example, if we consider the numbers 12 and 18, their common factors are 1, 2, 3, and 6. The largest of these is 6, so the GCF(12, 18) = 6.
Method 1: Prime Factorization
The prime factorization method is a powerful and intuitive way to find the GCF. It involves breaking down each number into its prime factors – the building blocks of numbers that are only divisible by 1 and themselves. Let's apply this method to find the GCF of 30 and 75:
1. Prime Factorization of 30:
30 can be broken down as follows:
30 = 2 × 15 = 2 × 3 × 5
Therefore, the prime factorization of 30 is 2 × 3 × 5.
2. Prime Factorization of 75:
75 can be broken down as follows:
75 = 3 × 25 = 3 × 5 × 5 = 3 × 5²
Therefore, the prime factorization of 75 is 3 × 5².
3. Identifying Common Factors:
Now, let's compare the prime factorizations of 30 and 75:
30 = 2 × 3 × 5 75 = 3 × 5²
The common prime factors are 3 and 5. Note that 3 appears once in both factorizations and 5 appears once in both factorizations as well.
4. Calculating the GCF:
To find the GCF, we multiply the common prime factors together, taking the lowest power of each common factor. In this case:
GCF(30, 75) = 3 × 5 = 15
Therefore, the greatest common factor of 30 and 75 is 15.
Method 2: The Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF, especially for larger numbers. This algorithm is based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. Let's apply it to 30 and 75:
1. Start with the larger number (75) and the smaller number (30):
75 ÷ 30 = 2 with a remainder of 15.
2. Replace the larger number (75) with the remainder (15):
Now we find the GCF of 30 and 15.
30 ÷ 15 = 2 with a remainder of 0.
3. The GCF is the last non-zero remainder:
Since the remainder is 0, the GCF is the previous remainder, which is 15.
Therefore, GCF(30, 75) = 15. The Euclidean algorithm provides a systematic and efficient approach, particularly beneficial when dealing with larger numbers where prime factorization might become cumbersome.
Method 3: Listing Factors
This method is suitable for smaller numbers and involves listing all the factors of each number and identifying the largest common factor.
1. List the factors of 30:
1, 2, 3, 5, 6, 10, 15, 30
2. List the factors of 75:
1, 3, 5, 15, 25, 75
3. Identify common factors:
The common factors of 30 and 75 are 1, 3, 5, and 15.
4. The GCF is the largest common factor:
The largest common factor is 15.
Therefore, GCF(30, 75) = 15. This method is straightforward but can become less efficient for larger numbers.
The Significance of the GCF
The GCF has significant applications in various areas of mathematics and beyond:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 30/75 can be simplified by dividing both the numerator and denominator by their GCF, 15, resulting in the simplified fraction 2/5.
-
Solving Diophantine Equations: Diophantine equations are algebraic equations where only integer solutions are sought. The GCF plays a vital role in determining the solvability of such equations.
-
Modular Arithmetic: In modular arithmetic (dealing with remainders after division), the GCF is used to determine the existence and number of solutions to congruences.
-
Computer Science: The Euclidean algorithm, used to find the GCF, is a fundamental algorithm in computer science and cryptography, particularly in RSA encryption.
-
Geometry and Measurement: The GCF is used in problems involving finding the largest possible square tile to cover a rectangular area.
Frequently Asked Questions (FAQ)
Q1: What is the difference between GCF and LCM?
The greatest common factor (GCF) is the largest number that divides both numbers evenly, while the least common multiple (LCM) is the smallest number that is a multiple of both numbers. They are related by the formula: GCF(a, b) × LCM(a, b) = a × b.
Q2: Can the GCF of two numbers be 1?
Yes, if two numbers have no common factors other than 1, their GCF is 1. Such numbers are called relatively prime or coprime.
Q3: How do I find the GCF of more than two numbers?
To find the GCF of more than two numbers, you can use the prime factorization method or repeatedly apply the Euclidean algorithm. Find the GCF of the first two numbers, then find the GCF of that result and the next number, and so on.
Q4: What if one of the numbers is zero?
The GCF of any number and zero is the absolute value of that number. For example, GCF(30, 0) = 30.
Q5: Is there a way to visualize the GCF?
You can visualize the GCF using area models. Imagine two rectangles with areas representing the two numbers. The GCF represents the area of the largest square that can perfectly tile both rectangles.
Conclusion
Finding the greatest common factor of 30 and 75, which we've determined to be 15, is not just a simple arithmetic exercise. It's an entry point into a deeper understanding of number theory, prime factorization, and the power of algorithms like the Euclidean algorithm. The GCF has far-reaching applications across diverse fields, highlighting its importance in mathematics and beyond. Mastering these methods equips you not only with a practical skill but also enhances your numerical reasoning abilities. Understanding the GCF is a stepping stone to appreciating the intricate beauty and structure hidden within the world of numbers.
Latest Posts
Latest Posts
-
Titration Curves Pogil Answer Key
Sep 18, 2025
-
Baby Boom Ap Human Geography
Sep 18, 2025
-
45 45 90 Practice Problems
Sep 18, 2025
-
Thirteen Colonies Map New England
Sep 18, 2025
-
Ap Computer Science Principles Textbook
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 30 And 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.