Gcf Of 35 And 15
zacarellano
Sep 15, 2025 · 6 min read
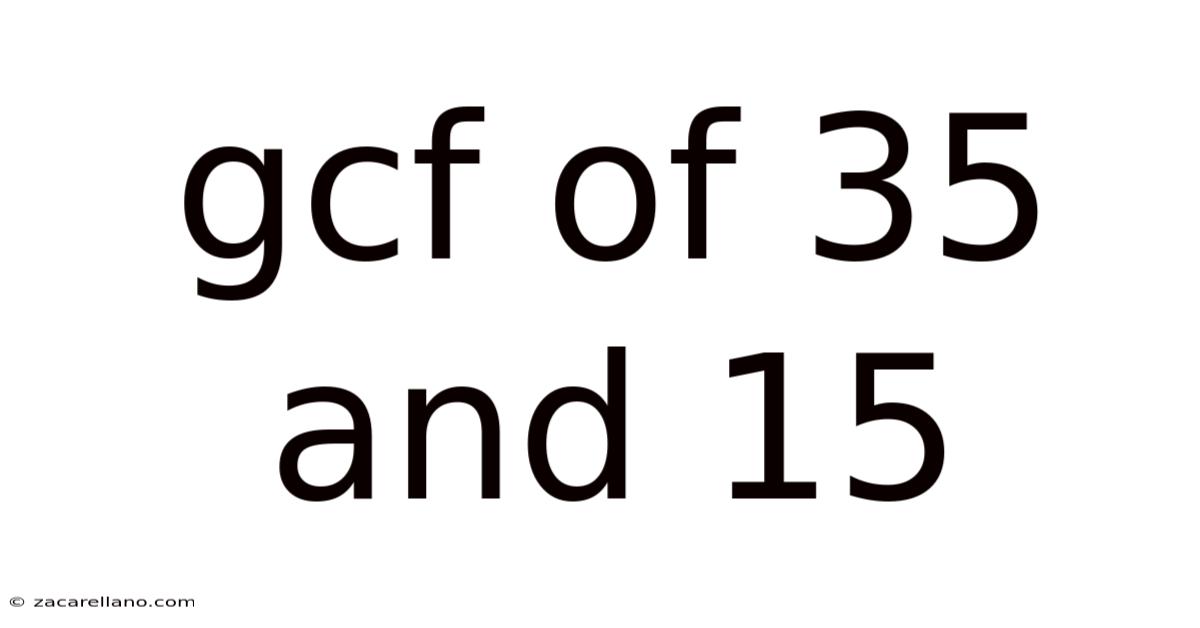
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 35 and 15: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles and various methods for calculating the GCF opens a door to a fascinating world of number theory with applications far beyond basic arithmetic. This article delves into the concept of GCF, specifically focusing on finding the GCF of 35 and 15, while exploring different approaches and explaining the mathematical rationale behind them. We’ll also explore the broader implications of GCF in mathematics and beyond.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without any remainder.
Finding the GCF is crucial in various mathematical operations, including simplifying fractions, solving algebraic equations, and understanding the relationships between numbers. It's a fundamental concept that underpins many more advanced mathematical concepts.
Methods for Finding the GCF of 35 and 15
Let's now focus on finding the GCF of 35 and 15. We'll explore several methods to illustrate the versatility and elegance of number theory.
1. Listing Factors Method
This is a straightforward approach, especially suitable for smaller numbers. We list all the factors of each number and then identify the largest common factor.
- Factors of 15: 1, 3, 5, 15
- Factors of 35: 1, 5, 7, 35
By comparing the two lists, we see that the common factors are 1 and 5. The largest of these is 5. Therefore, the GCF of 15 and 35 is 5.
This method is simple and intuitive, but it becomes less efficient as the numbers get larger. Imagine trying to list all factors of a number like 1470!
2. Prime Factorization Method
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers (numbers divisible only by 1 and themselves).
- Prime factorization of 15: 3 x 5
- Prime factorization of 35: 5 x 7
Once we have the prime factorization, we identify the common prime factors and multiply them together. Both 15 and 35 share the prime factor 5. Therefore, the GCF of 15 and 35 is 5.
This method is more efficient than listing all factors, particularly for larger numbers. It provides a deeper understanding of the numerical relationships involved.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially large ones. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Let's apply the Euclidean algorithm to 35 and 15:
- Step 1: 35 - 15 = 20. Now we find the GCF of 15 and 20.
- Step 2: 20 - 15 = 5. Now we find the GCF of 15 and 5.
- Step 3: 15 - (5 x 3) = 0. Since we've reached 0, the GCF is the last non-zero remainder, which is 5.
The Euclidean algorithm is remarkably efficient because it systematically reduces the numbers involved, avoiding the need for complete factorization. It's the preferred method for large numbers where listing factors or prime factorization would be impractical.
4. Ladder Method (Division Method)
The ladder method involves repeatedly dividing the larger number by the smaller number until the remainder is zero. The last non-zero remainder is the GCF.
- Divide 35 by 15: 35 ÷ 15 = 2 with a remainder of 5.
- Now divide 15 by the remainder 5: 15 ÷ 5 = 3 with a remainder of 0.
Since the remainder is 0, the GCF is the last non-zero remainder, which is 5. This method is similar in efficiency to the Euclidean algorithm and provides a clear, step-by-step approach.
Mathematical Significance of GCF
The concept of GCF extends far beyond simply finding the largest common divisor of two numbers. It plays a vital role in various areas of mathematics:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 15/35 can be simplified by dividing both the numerator and the denominator by their GCF (5), resulting in the equivalent fraction 3/7.
-
Solving Diophantine Equations: These are algebraic equations where only integer solutions are sought. The GCF is often crucial in determining the existence and nature of solutions.
-
Modular Arithmetic: In modular arithmetic (working with remainders after division), the GCF plays a significant role in determining invertibility and solving congruences.
-
Abstract Algebra: The concept of GCF is generalized in abstract algebra to the notion of greatest common divisor in rings and other algebraic structures.
-
Cryptography: GCF, specifically the Euclidean Algorithm, is a crucial component of several cryptographic algorithms, including RSA, a widely used public-key cryptosystem.
Applications of GCF Beyond Mathematics
While the mathematical applications are significant, the GCF also has practical applications in various fields:
-
Measurement and Geometry: When dealing with lengths or areas, finding the GCF can help in determining the largest possible unit of measurement that can divide lengths or areas without leaving a remainder.
-
Manufacturing and Production: In manufacturing, the GCF can determine the maximum size of identical items that can be cut from a larger piece of material. For example, if you have two pieces of wood of length 35cm and 15cm, the largest identical pieces you can cut are 5cm long.
-
Scheduling and Planning: Finding the common factors can be useful in scheduling events or tasks that must occur at regular intervals. The GCF helps identify the longest common interval at which these events can occur simultaneously.
Frequently Asked Questions (FAQ)
-
Q: What if the GCF of two numbers is 1?
- A: If the GCF of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they share no common factors other than 1.
-
Q: Can I find the GCF of more than two numbers?
- A: Yes, you can extend the methods discussed above to find the GCF of more than two numbers. You can find the GCF of two of the numbers, then find the GCF of that result and the next number, and so on.
-
Q: Which method is the best for finding the GCF?
- A: The best method depends on the size of the numbers. For small numbers, listing factors is easiest. For larger numbers, the Euclidean algorithm or prime factorization is more efficient. The Ladder method offers a good balance between simplicity and efficiency.
Conclusion
Finding the greatest common factor of 35 and 15, which is 5, is not just a simple arithmetic exercise. It's a gateway to understanding fundamental concepts in number theory and their broad implications in mathematics and beyond. Whether you use the listing factors method, prime factorization, the Euclidean algorithm, or the Ladder Method, understanding the underlying principles allows you to appreciate the elegance and efficiency of these techniques. The GCF isn't just a number; it's a key that unlocks a deeper understanding of numerical relationships and their practical applications in various fields. From simplifying fractions to aiding in complex cryptographic systems, the GCF reveals its importance in the fabric of mathematics and its real-world relevance.
Latest Posts
Latest Posts
-
Find The Indicated Z Score
Sep 15, 2025
-
Derivative Of Cos X 3
Sep 15, 2025
-
What Is A Precapillary Sphincter
Sep 15, 2025
-
Theme Examples In A Story
Sep 15, 2025
-
What Is The American Ideal
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 35 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.