Gcf Of 40 And 16
zacarellano
Sep 05, 2025 · 6 min read
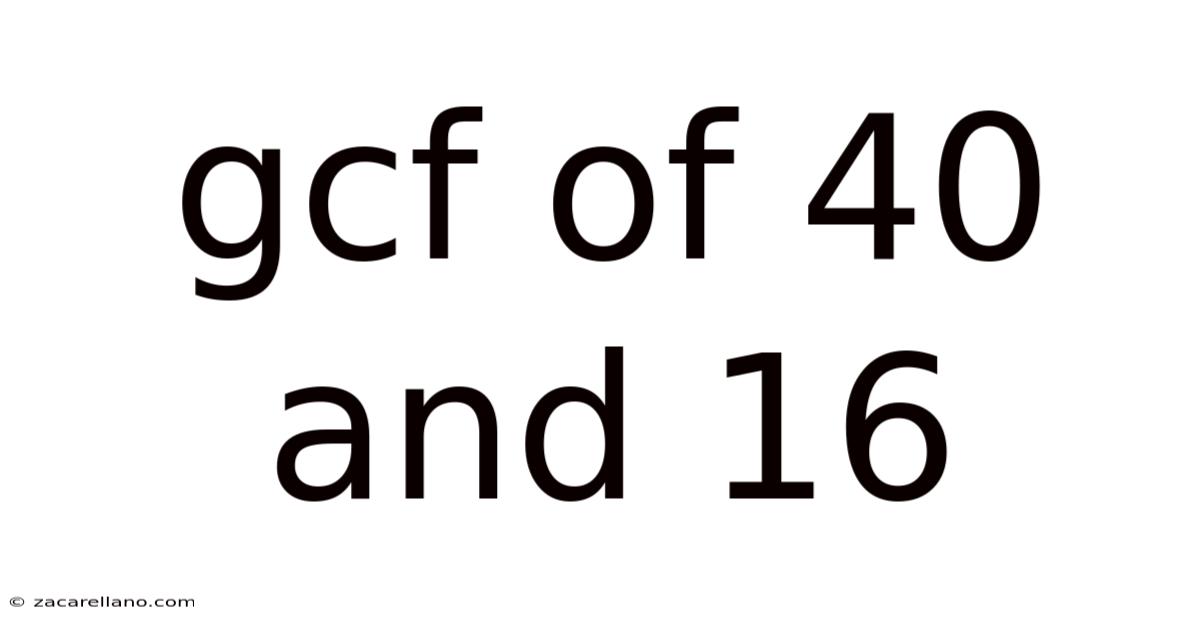
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 40 and 16: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. This article will thoroughly explore how to determine the GCF of 40 and 16, using multiple methods. We'll delve into the underlying principles of number theory, ensuring you not only understand the answer but also grasp the broader context and applications of this crucial mathematical operation. Understanding GCFs is crucial for simplifying fractions, solving algebraic equations, and even understanding more advanced mathematical concepts.
Introduction: What is the Greatest Common Factor (GCF)?
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. For instance, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder. This article focuses specifically on finding the GCF of 40 and 16.
Method 1: Listing Factors
This method involves listing all the factors of each number and then identifying the largest factor common to both.
Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
Factors of 16: 1, 2, 4, 8, 16
By comparing the two lists, we can see that the common factors are 1, 2, 4, and 8. The largest of these common factors is 8. Therefore, the GCF of 40 and 16 is 8.
Method 2: Prime Factorization
This is a more systematic and generally preferred method, especially for larger numbers. It involves expressing each number as a product of its prime factors. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself (e.g., 2, 3, 5, 7, 11...).
Prime Factorization of 40:
We can break down 40 into its prime factors as follows:
40 = 2 x 20 = 2 x 2 x 10 = 2 x 2 x 2 x 5 = 2³ x 5
Prime Factorization of 16:
Similarly, we can find the prime factors of 16:
16 = 2 x 8 = 2 x 2 x 4 = 2 x 2 x 2 x 2 = 2⁴
Now, to find the GCF, we identify the common prime factors and take the lowest power of each. Both 40 and 16 have 2 as a prime factor. The lowest power of 2 present in both factorizations is 2³. Therefore:
GCF(40, 16) = 2³ = 8
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, particularly useful for larger numbers where listing factors or prime factorization becomes cumbersome. This algorithm is based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Let's apply the Euclidean algorithm to find the GCF of 40 and 16:
- Divide the larger number (40) by the smaller number (16) and find the remainder:
40 ÷ 16 = 2 with a remainder of 8
- Replace the larger number (40) with the smaller number (16) and the smaller number with the remainder (8):
Now we find the GCF of 16 and 8.
- Repeat the process:
16 ÷ 8 = 2 with a remainder of 0
Since the remainder is 0, the GCF is the last non-zero remainder, which is 8.
Understanding the Significance of the GCF
The GCF has numerous applications across various mathematical fields and real-world scenarios:
-
Simplifying Fractions: The GCF allows us to simplify fractions to their lowest terms. For example, the fraction 40/16 can be simplified by dividing both the numerator and the denominator by their GCF (8), resulting in the simplified fraction 5/2.
-
Solving Equations: The GCF plays a role in solving Diophantine equations, which are equations where only integer solutions are sought.
-
Geometry: The GCF is used in problems involving geometric figures with integer dimensions, such as finding the dimensions of the largest square tile that can perfectly cover a rectangular floor.
-
Number Theory: The GCF forms the foundation of various concepts in number theory, including modular arithmetic and the study of prime numbers.
-
Computer Science: The Euclidean algorithm, used to calculate the GCF, is a cornerstone of many algorithms in computer science, particularly in cryptography and data analysis.
Extending the Concept: GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For prime factorization, we consider all the prime factors common to all the numbers and take the lowest power of each common prime factor. For the Euclidean algorithm, we can iteratively find the GCF of pairs of numbers until we obtain the GCF of all the numbers. For example, to find the GCF of 40, 16, and 24, we can first find the GCF of 40 and 16 (which is 8), and then find the GCF of 8 and 24 (which is 8). Thus, the GCF of 40, 16, and 24 is 8.
Frequently Asked Questions (FAQ)
Q1: What is the difference between GCF and LCM?
The GCF (Greatest Common Factor) is the largest number that divides evenly into two or more numbers. The LCM (Least Common Multiple) is the smallest number that is a multiple of two or more numbers. They are related inversely; for two numbers a and b, GCF(a, b) * LCM(a, b) = a * b.
Q2: Why is the prime factorization method considered efficient?
The prime factorization method is efficient because it breaks down the numbers into their fundamental building blocks. Once we have the prime factorization, finding the GCF becomes a simple matter of identifying common prime factors and taking the lowest powers. This is particularly beneficial for larger numbers where listing all factors would be time-consuming.
Q3: Can the Euclidean algorithm be used for non-integer numbers?
The standard Euclidean algorithm is designed for integers. However, there are extensions and modifications of the algorithm that can be applied to other number systems, including rational numbers and polynomials.
Q4: What if the GCF of two numbers is 1?
If the GCF of two numbers is 1, it means the two numbers are relatively prime or coprime. This signifies that they share no common factors other than 1.
Q5: Are there any online calculators or tools to find the GCF?
Yes, many online calculators and mathematical software packages can compute the GCF of two or more numbers. These tools can be helpful for verifying results or handling larger numbers.
Conclusion: Mastering the GCF
Finding the greatest common factor is a crucial skill in mathematics with far-reaching applications. We've explored three different methods—listing factors, prime factorization, and the Euclidean algorithm—to determine the GCF of 40 and 16, which is 8. Understanding these methods provides a strong foundation for tackling more complex problems in number theory, algebra, and various other fields. The choice of method often depends on the size of the numbers involved and the context of the problem. By mastering the concepts presented here, you'll not only be able to calculate GCFs effectively but also appreciate their significance in the broader landscape of mathematics. Remember that practice is key to solidifying your understanding and developing proficiency in finding the greatest common factor.
Latest Posts
Latest Posts
-
Inequalities Variables On Both Sides
Sep 05, 2025
-
What Is An Exponential Relationship
Sep 05, 2025
-
Trp Operon Vs Lac Operon
Sep 05, 2025
-
2 Lb How Many Oz
Sep 05, 2025
-
Algebra And Functions Practice Test
Sep 05, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 40 And 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.