Gcf Of 8 And 3
zacarellano
Sep 18, 2025 · 6 min read
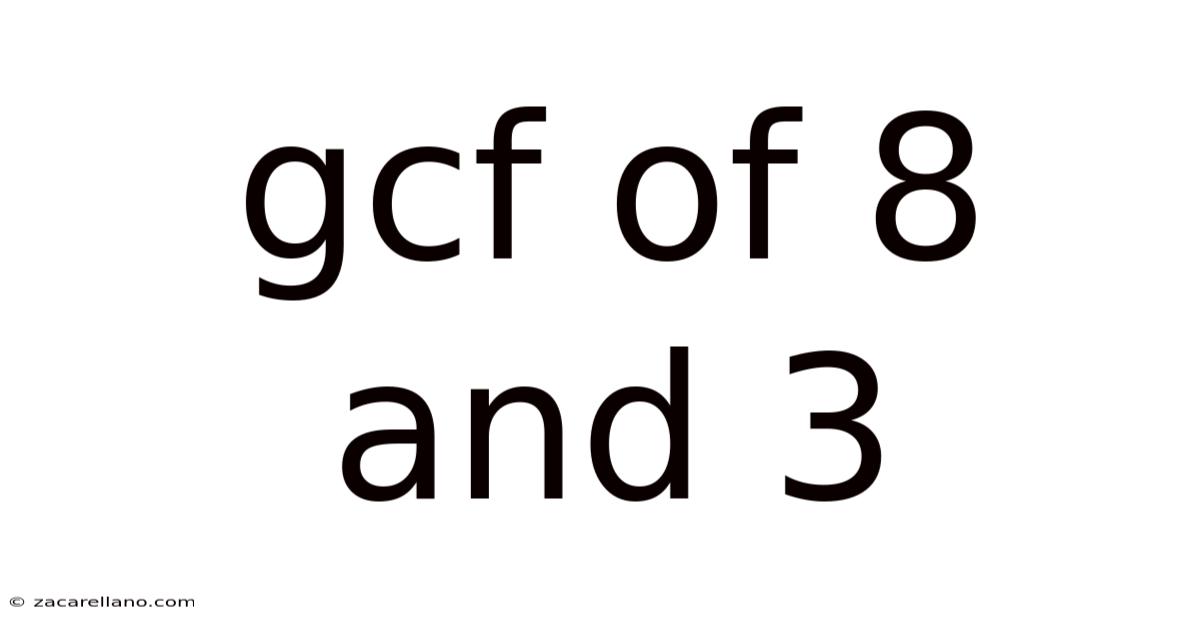
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 8 and 3: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple task, especially when dealing with small numbers like 8 and 3. However, understanding the underlying principles behind GCF calculation opens doors to a fascinating world of number theory and its practical applications in mathematics and computer science. This article will delve into the GCF of 8 and 3, explaining various methods to find it, exploring the theoretical concepts involved, and answering frequently asked questions. By the end, you'll not only know the GCF of 8 and 3 but also possess a solid foundation in understanding GCF calculations for any pair of numbers.
Introduction: What is the Greatest Common Factor (GCF)?
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. For instance, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder. Understanding GCF is crucial in simplifying fractions, solving algebraic equations, and various other mathematical applications.
Finding the GCF of 8 and 3: Methods and Explanations
Let's explore different methods to determine the GCF of 8 and 3. While the answer might seem immediately obvious for such small numbers, understanding these methods is essential for tackling larger and more complex numbers.
1. Listing Factors Method:
This method involves listing all the factors of each number and then identifying the largest factor common to both.
- Factors of 8: 1, 2, 4, 8
- Factors of 3: 1, 3
Comparing the two lists, we see that the only common factor is 1. Therefore, the GCF of 8 and 3 is 1.
2. Prime Factorization Method:
This method utilizes the prime factorization of each number. Prime factorization involves expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 3: 3 (3 is a prime number)
Since there are no common prime factors between 8 and 3, their GCF is 1. This method is particularly useful for larger numbers where listing factors becomes cumbersome.
3. Euclidean Algorithm:
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 8 and 3:
- 8 - 3 = 5
- 5 - 3 = 2
- 3 - 2 = 1
- 2 - 1 = 1
The algorithm stops when we reach 1. Therefore, the GCF of 8 and 3 is 1. This method is particularly efficient for larger numbers because it reduces the numbers involved at each step.
Why is the GCF of 8 and 3 equal to 1? A Deeper Look
The GCF of 8 and 3 being 1 signifies that these two numbers are relatively prime or coprime. Relatively prime numbers share no common factors other than 1. This means that their greatest common divisor is 1. The fact that 8 is an even number (divisible by 2) and 3 is an odd number (not divisible by 2) already hints at their lack of common factors beyond 1. Furthermore, 3 is a prime number, meaning its only divisors are 1 and itself. Since neither 2 nor any power of 2 is a factor of 3, it's clear that 8 and 3 share only the trivial common factor of 1.
Practical Applications of GCF
Understanding and calculating the GCF has several practical applications in various fields:
-
Simplifying Fractions: The GCF is essential for simplifying fractions to their lowest terms. For example, to simplify the fraction 12/18, we find the GCF of 12 and 18 (which is 6) and divide both the numerator and denominator by 6 to get the simplified fraction 2/3.
-
Solving Diophantine Equations: Diophantine equations are algebraic equations where only integer solutions are sought. Finding the GCF is crucial in determining the existence and finding solutions to certain types of Diophantine equations.
-
Cryptography: GCF and related concepts play a significant role in various cryptographic algorithms, contributing to secure data transmission and storage.
-
Computer Science: The Euclidean algorithm for finding the GCF is a fundamental algorithm used in computer science for various applications, including optimizing computations and simplifying complex data structures.
-
Modular Arithmetic: GCF is a cornerstone in understanding concepts like modular arithmetic, which is used extensively in cryptography and coding theory.
Frequently Asked Questions (FAQ)
Q1: What if I have more than two numbers? How do I find the GCF?
A1: To find the GCF of more than two numbers, you can extend any of the methods discussed above. For the prime factorization method, you would find the prime factorization of each number and then identify the common prime factors raised to the lowest power. For the Euclidean algorithm, you would repeatedly apply the algorithm to pairs of numbers until you arrive at the GCF.
Q2: Is there a formula for calculating the GCF?
A2: There isn't a single, universally applicable formula for calculating the GCF for any two numbers. The methods described above (listing factors, prime factorization, and the Euclidean algorithm) provide systematic approaches to finding the GCF.
Q3: Why is the GCF important in simplifying fractions?
A3: Simplifying fractions to their lowest terms ensures efficiency and clarity. Dividing both the numerator and the denominator by their GCF results in an equivalent fraction that is easier to work with in calculations and comparisons.
Q4: Are all pairs of numbers relatively prime?
A4: No, not all pairs of numbers are relatively prime. Only pairs of numbers that share no common factors other than 1 are considered relatively prime. For example, 15 and 25 are not relatively prime because their GCF is 5.
Q5: Can the GCF of two numbers ever be greater than either of the numbers?
A5: No. The GCF is always less than or equal to the smaller of the two numbers. It's the greatest common factor, and it cannot exceed the size of either of the numbers it divides.
Conclusion: Beyond the Simple Calculation
While finding the GCF of 8 and 3 might seem trivial, the process highlights fundamental concepts in number theory. Understanding the different methods for calculating the GCF, such as listing factors, prime factorization, and the Euclidean algorithm, provides a strong foundation for tackling more complex problems. The applications of GCF extend far beyond simple arithmetic, encompassing significant roles in various branches of mathematics and computer science. This deep dive into the seemingly simple calculation of the GCF of 8 and 3 has hopefully broadened your understanding of this important concept and its widespread applications. The next time you encounter a GCF problem, remember the underlying principles and the various approaches available to solve it efficiently. Remember, mathematical proficiency isn't just about getting the right answer; it's about understanding the why behind the answer, leading to a deeper appreciation of the elegant structures within mathematics.
Latest Posts
Latest Posts
-
What Is The Central Theme
Sep 18, 2025
-
Math Problems For College Students
Sep 18, 2025
-
Ionic Compound Nonmetal And Metal
Sep 18, 2025
-
What Is Sin Of 90
Sep 18, 2025
-
List The Factors Of 7
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 8 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.