Integral Of 1 5 X
zacarellano
Sep 24, 2025 · 6 min read
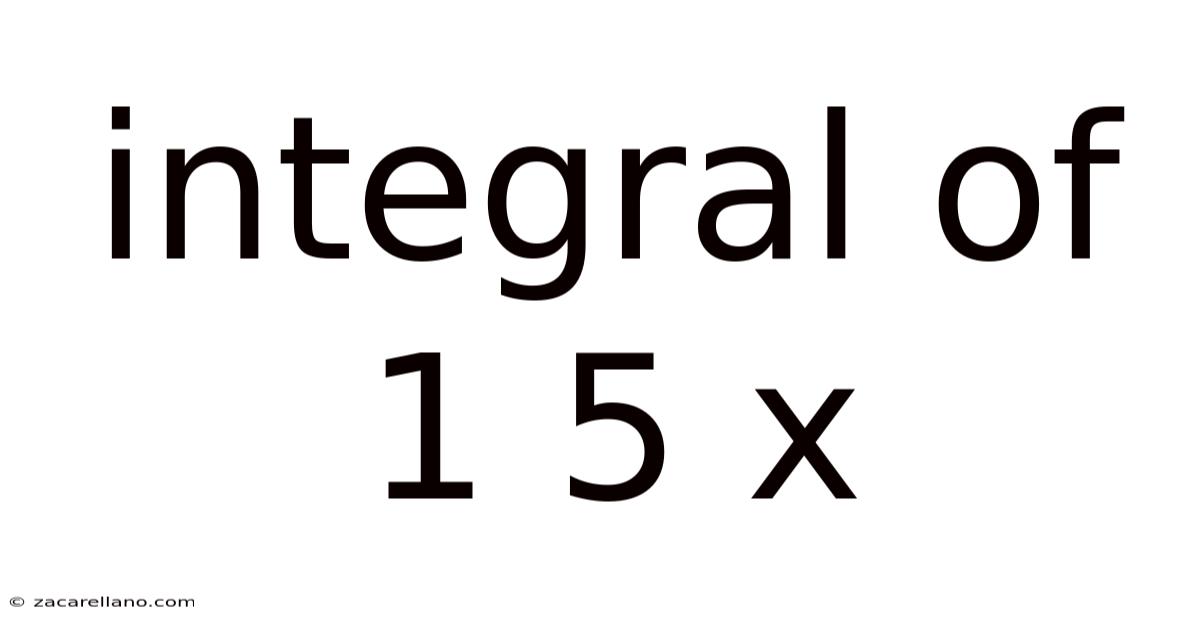
Table of Contents
Understanding and Solving the Integral of 1/(5x)
This article delves into the intricacies of solving the indefinite integral of 1/(5x), a fundamental concept in calculus. We'll break down the process step-by-step, providing a clear and comprehensive explanation suitable for students of various mathematical backgrounds. We'll explore the underlying principles, address common misconceptions, and even tackle some frequently asked questions. Understanding this seemingly simple integral is crucial for mastering more complex integration techniques later on. The keyword here is indefinite integral, as we're not dealing with defined limits of integration.
Introduction: The Indefinite Integral
Before diving into the specific problem, let's establish a firm understanding of what an indefinite integral represents. In simple terms, an indefinite integral is the reverse process of differentiation. While differentiation finds the instantaneous rate of change of a function, integration finds the function whose derivative is the given function. We represent the indefinite integral using the integral symbol ∫, followed by the function and dx, indicating integration with respect to x. The result is a family of functions (differing only by a constant) whose derivatives all equal the original function. This constant is denoted as "+C".
Step-by-Step Solution: Solving the Integral of 1/(5x)
The problem at hand is to evaluate ∫(1/(5x)) dx. Here’s how we approach it:
-
Constant Multiple Rule: The first step involves utilizing the constant multiple rule of integration, which states that the integral of a constant times a function is equal to the constant times the integral of the function. In our case, the constant is 1/5. Therefore, we can rewrite the integral as:
(1/5) ∫(1/x) dx
-
Integral of 1/x: The core of this problem lies in recognizing the integral of 1/x. This is a crucial integral to remember, as it doesn't follow the standard power rule of integration (which applies to x<sup>n</sup> where n ≠ -1). The integral of 1/x is the natural logarithm of the absolute value of x, denoted as ln|x|. The absolute value is crucial here because the natural logarithm is only defined for positive arguments.
-
Putting it Together: Now, let’s combine the constant multiple rule and the integral of 1/x:
(1/5) ∫(1/x) dx = (1/5) ln|x| + C
Therefore, the indefinite integral of 1/(5x) is (1/5)ln|x| + C, where C is the constant of integration.
Explanation: Why the Natural Logarithm?
The appearance of the natural logarithm might seem unexpected. To understand why, let's consider the derivative of ln|x|:
The derivative of ln(x) for x > 0 is 1/x. For x < 0, we have ln(-x), and using the chain rule, its derivative is (1/(-x)) * (-1) = 1/x. Therefore, the derivative of ln|x| is 1/x for all x ≠ 0. This confirms that the antiderivative (integral) of 1/x is ln|x| + C.
Common Mistakes and Misconceptions
Several common mistakes can occur when solving integrals involving 1/x or similar functions. Here are a few to watch out for:
-
Forgetting the Absolute Value: Omitting the absolute value bars in ln|x| is a frequent error. Remember, the natural logarithm is only defined for positive arguments. The absolute value ensures the function is defined for both positive and negative values of x.
-
Incorrect Application of Power Rule: Students often mistakenly try to apply the power rule of integration (∫x<sup>n</sup> dx = (x<sup>n+1</sup>)/(n+1) + C) directly to 1/x (which is x<sup>-1</sup>). However, the power rule is invalid when n = -1, hence the need for the natural logarithm.
-
Neglecting the Constant of Integration: Forgetting the "+C" is another common mistake. This constant represents the family of functions that all have the same derivative. Leaving it out leads to an incomplete and incorrect solution.
Further Exploration: Definite Integrals and Applications
While this article focuses on the indefinite integral, it's important to understand the concept of definite integrals as well. A definite integral has defined limits of integration (a and b), represented as:
∫<sub>a</sub><sup>b</sup> (1/(5x)) dx
Evaluating a definite integral involves finding the antiderivative, substituting the upper and lower limits, and subtracting the results. This provides a numerical value representing the area under the curve of the function between the limits a and b.
The integral of 1/(5x) finds application in various fields, including:
-
Physics: Solving problems related to radioactive decay, where the rate of decay is proportional to the amount of substance remaining.
-
Chemistry: Modeling chemical reactions where the rate of reaction depends on the concentration of reactants.
-
Economics: Analyzing growth and decay models, such as compound interest or population dynamics.
Frequently Asked Questions (FAQ)
Q1: What if the integral was ∫(1/(5x + 2)) dx?
A1: This requires a slightly different approach. You would use u-substitution, letting u = 5x + 2 and du = 5dx. This would transform the integral into (1/5)∫(1/u) du = (1/5)ln|u| + C. Substituting back for u, the result would be (1/5)ln|5x + 2| + C.
Q2: Can we integrate 1/x from -1 to 1?
A2: No, we cannot directly integrate 1/x from -1 to 1. The function 1/x has a discontinuity (a vertical asymptote) at x = 0, which lies within the interval [-1, 1]. Improper integral techniques are required to handle this situation.
Q3: What is the significance of the constant of integration, C?
A3: The constant of integration represents the family of functions that all have the same derivative. Since the derivative of a constant is zero, adding any constant to the antiderivative does not change its derivative. The specific value of C depends on the initial conditions or boundary conditions of the problem.
Q4: Why is the absolute value necessary in ln|x|?
A4: The natural logarithm is only defined for positive arguments. The absolute value ensures that the argument of the logarithm is always positive, regardless of whether x is positive or negative. This extends the domain of the antiderivative to all x except x=0.
Conclusion: Mastering the Fundamentals
The integral of 1/(5x) might seem deceptively simple, but mastering its solution is crucial for building a strong foundation in calculus. Understanding the constant multiple rule, recognizing the integral of 1/x as ln|x|, and remembering the significance of the absolute value and the constant of integration are key takeaways. By carefully considering the underlying principles and avoiding common pitfalls, you'll be well-equipped to tackle more challenging integration problems in the future. This fundamental integral serves as a stepping stone to more advanced integration techniques and applications across various scientific and engineering disciplines. Remember to practice consistently and explore different problem variations to solidify your understanding.
Latest Posts
Latest Posts
-
Constitutional Isomers Vs Geometric Isomers
Sep 24, 2025
-
Is 21 Prime Or Composite
Sep 24, 2025
-
4th Grade Fraction Word Problems
Sep 24, 2025
-
Does Anp Increase Blood Pressure
Sep 24, 2025
-
Resolving Vector Components With Trigonometry
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 5 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.