Is 1/2 Greater Than 1
zacarellano
Sep 18, 2025 · 5 min read
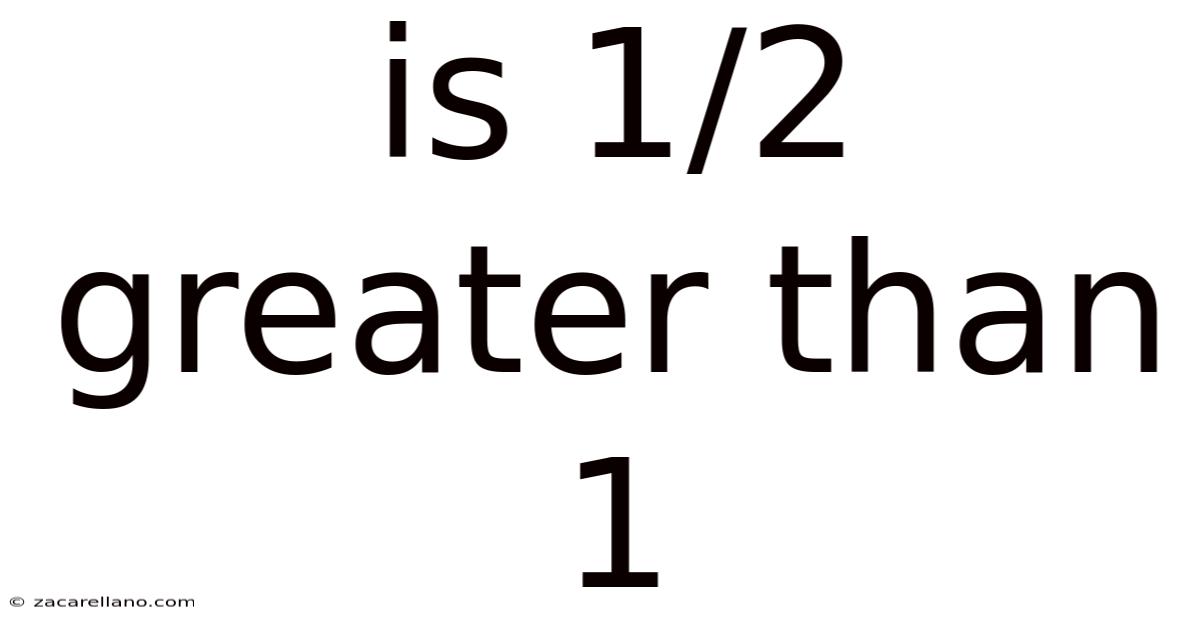
Table of Contents
Is 1/2 Greater Than 1? Understanding Fractions and Comparisons
Is 1/2 greater than 1? The answer, at first glance, seems obvious: no. But understanding why requires a deeper dive into the world of fractions and numerical comparison. This article will explore the concept of fractions, explain how to compare them, and delve into the reasoning behind why 1/2 is not greater than 1. We will also address common misconceptions and provide practical examples to solidify your understanding.
Understanding Fractions: Parts of a Whole
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
For example, in the fraction 1/2, the denominator (2) means the whole is divided into two equal parts. The numerator (1) indicates we're considering one of those two parts. Visually, imagine a pizza cut into two equal slices. 1/2 represents one of those slices.
Other examples include:
- 1/4: One out of four equal parts. Think of a quarter of a dollar or a pizza cut into four slices.
- 3/4: Three out of four equal parts. Three-quarters of a pizza.
- 2/3: Two out of three equal parts. Two-thirds of a chocolate bar.
Comparing Fractions: Determining Greater Than, Less Than, or Equal To
Comparing fractions involves determining which fraction represents a larger portion of the whole. There are several ways to do this:
1. Common Denominator Method: This is the most common and reliable method. If two fractions have the same denominator, the fraction with the larger numerator is the larger fraction. For example, 3/5 > 2/5 because 3 > 2.
If the fractions have different denominators, you need to find a common denominator – a number that is a multiple of both denominators. Then, convert both fractions to equivalent fractions with the common denominator and compare the numerators.
Let's compare 1/2 and 3/4:
- The common denominator of 2 and 4 is 4.
- Convert 1/2 to an equivalent fraction with a denominator of 4: (1 x 2) / (2 x 2) = 2/4
- Now compare 2/4 and 3/4. Since 2 < 3, 2/4 < 3/4, therefore 1/2 < 3/4.
2. Visual Representation: Drawing diagrams, like circles or rectangles divided into equal parts, can be helpful for visualizing and comparing fractions. This method is particularly useful for beginners.
3. Decimal Conversion: Convert both fractions into decimals and compare the decimal values. For example, 1/2 = 0.5 and 3/4 = 0.75. Since 0.5 < 0.75, 1/2 < 3/4.
Why 1/2 is Not Greater Than 1
Using any of the methods above, it's clear that 1/2 is not greater than 1.
-
Common Denominator: If we try to find a common denominator for 1/2 and 1 (which can be written as 1/1), the common denominator is 2. 1/2 remains 1/2, while 1/1 becomes 2/2. Since 1 < 2, 1/2 < 2/2, therefore 1/2 < 1.
-
Visual Representation: Imagine a single whole object (like a cake). 1/2 represents half the cake, while 1 represents the entire cake. Clearly, half a cake is less than a whole cake.
-
Decimal Conversion: 1/2 converts to 0.5, while 1 converts to 1.0. 0.5 < 1.0, confirming that 1/2 < 1.
Common Misconceptions about Fractions
Several common misconceptions can lead to confusion when working with fractions:
-
Larger Numerator Means Larger Fraction: This is only true if the denominators are the same. For example, 5/8 > 3/8, but 5/8 < 7/10.
-
Ignoring the Denominator: The denominator is crucial in determining the size of the fraction. It represents the total number of parts the whole is divided into.
-
Adding Numerators and Denominators: You cannot simply add the numerator and denominator to compare fractions. For example, 1/2 + 1/3 is not equal to 2/5.
-
Confusing Fractions with Whole Numbers: Fractions represent parts of a whole, not whole numbers themselves.
Real-World Applications of Fraction Comparison
Understanding fraction comparison is essential in many real-world scenarios:
-
Cooking and Baking: Recipes often require precise measurements using fractions (e.g., 1/2 cup of sugar, 1/4 teaspoon of salt).
-
Construction and Engineering: Accurate measurements are critical in these fields, and fractions are commonly used to represent dimensions and quantities.
-
Finance: Fractions are used extensively in finance to represent percentages, ratios, and proportions (e.g., interest rates, stock prices).
-
Data Analysis: Fractions can represent proportions and percentages in data analysis, helping to understand trends and patterns.
Frequently Asked Questions (FAQ)
Q: Can a fraction be greater than 1?
A: Yes, a fraction can be greater than 1. This occurs when the numerator is larger than the denominator (e.g., 5/4, 7/3). These are called improper fractions. They can also be expressed as mixed numbers (e.g., 1 ¼, 2 ⅓).
Q: How do I convert an improper fraction to a mixed number?
A: Divide the numerator by the denominator. The quotient is the whole number part of the mixed number, and the remainder is the numerator of the fractional part. The denominator remains the same. For example, 5/4 = 1 remainder 1, so 5/4 = 1 ¼.
Q: How do I convert a mixed number to an improper fraction?
A: Multiply the whole number by the denominator, add the numerator, and keep the same denominator. For example, 1 ¼ = (1 x 4 + 1)/4 = 5/4.
Q: What are equivalent fractions?
A: Equivalent fractions represent the same proportion of a whole, even though they look different. For example, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions.
Conclusion
In conclusion, 1/2 is definitively not greater than 1. Understanding fractions and the different methods for comparing them is crucial for various aspects of life. By grasping the fundamental concepts and addressing common misconceptions, you can confidently work with fractions and apply this knowledge to solve real-world problems. Remember the significance of both the numerator and the denominator, and use the strategies outlined – common denominators, visual representation, or decimal conversion – to accurately compare fractions and understand their relative values. With practice and a solid understanding of the basics, working with fractions will become intuitive and straightforward.
Latest Posts
Latest Posts
-
Second Grade Math Word Problems
Sep 18, 2025
-
Natural Rights Definition Ap Gov
Sep 18, 2025
-
Forma Estandar De Un Numero
Sep 18, 2025
-
James Lange Vs Schachter Singer
Sep 18, 2025
-
Is Velocity Derivative Of Position
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Is 1/2 Greater Than 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.