Is -1/2 Smaller Than -3/2
zacarellano
Sep 15, 2025 · 5 min read
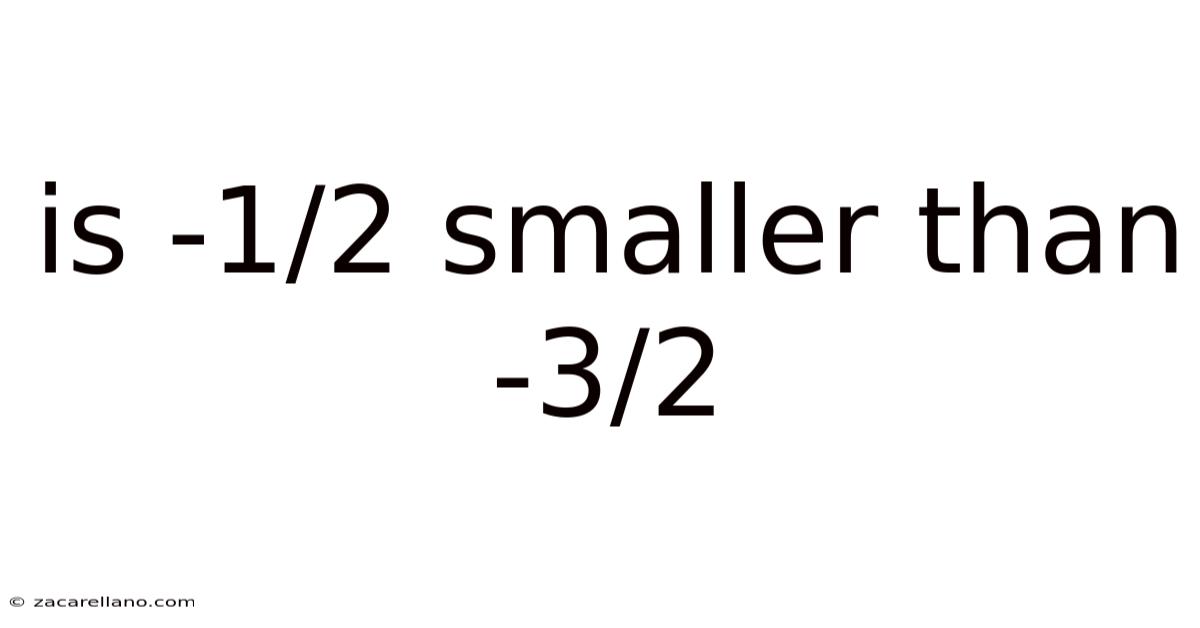
Table of Contents
Is -1/2 Smaller Than -3/2? Understanding Negative Numbers on the Number Line
Are you struggling to compare negative fractions? Many find comparing numbers with negative signs confusing. This comprehensive guide will not only answer the question, "Is -1/2 smaller than -3/2?" but also equip you with the understanding to compare any negative numbers with confidence. We'll explore the number line, delve into the concept of magnitude, and provide practical examples to solidify your understanding.
Understanding the Number Line
The number line is a fundamental tool in mathematics used to visualize and compare numbers. It's a horizontal line with zero at the center. Positive numbers are located to the right of zero, and negative numbers are to the left. The further a number is from zero, the greater its magnitude or absolute value.
Imagine a number line stretching infinitely in both directions. Zero sits comfortably in the middle. To the right, we have positive numbers: 1, 2, 3, and so on. To the left, we encounter negative numbers: -1, -2, -3, and so forth.
Comparing Positive Numbers
Comparing positive numbers is straightforward. The number further to the right on the number line is greater. For example, 5 is greater than 3 (5 > 3).
Comparing Negative Numbers: The Twist
Now, let's consider negative numbers. The rule flips! The number further to the left on the number line is smaller. This is where many encounter confusion. Let's illustrate this with our initial question: Is -1/2 smaller than -3/2?
Visualizing -1/2 and -3/2 on the Number Line
Imagine plotting -1/2 and -3/2 on the number line. -1/2 would be located halfway between 0 and -1. -3/2, or -1.5, would be located halfway between -1 and -2.
Since -3/2 is further to the left than -1/2, it is smaller. Therefore, yes, -1/2 is greater than -3/2. We can write this as: -1/2 > -3/2.
The Concept of Magnitude (Absolute Value) and its Role in Comparison
While the position on the number line dictates the order of negative numbers, the magnitude or absolute value refers to the distance of a number from zero, regardless of its sign. The absolute value of a number is always positive or zero. It is denoted by vertical bars: |x|.
For example:
- |3| = 3
- |-3| = 3
- |-1/2| = 1/2
- |-3/2| = 3/2
Although |-3/2| (1.5) is greater than |-1/2| (0.5), this doesn't mean -3/2 is greater than -1/2. Magnitude only tells us the distance from zero; it doesn't dictate the order on the number line for negative numbers. Remember, for negative numbers, the number further to the left is the smaller number.
Working with Fractions: A Step-by-Step Approach
Comparing fractions, especially negative ones, can sometimes feel tricky. Here's a step-by-step approach:
-
Find a Common Denominator: If the fractions have different denominators, find the least common multiple (LCM) of the denominators. This ensures that you are comparing apples to apples.
-
Convert to Equivalent Fractions: Rewrite the fractions with the common denominator.
-
Compare Numerators: Once the denominators are the same, compare the numerators. The fraction with the smaller numerator is the smaller fraction. Remember, this rule applies to positive fractions but reverses for negative fractions.
Example: Let's compare -1/2 and -3/4.
-
Common Denominator: The LCM of 2 and 4 is 4.
-
Equivalent Fractions: -1/2 is equivalent to -2/4.
-
Compare Numerators: Now we compare -2/4 and -3/4. Since -3 is less than -2, -3/4 is less than -2/4. Therefore, -3/4 < -1/2.
Practical Examples: Real-World Application
Understanding the comparison of negative numbers extends beyond theoretical exercises. It has real-world applications in various fields:
-
Finance: Representing debts or losses. A debt of -$300 is greater than a debt of -$100. The larger negative number represents a larger debt.
-
Temperature: Comparing temperatures below zero. A temperature of -5°C is colder (smaller) than -2°C.
-
Elevation: Describing altitudes below sea level. An elevation of -10 meters is lower (smaller) than -5 meters.
Frequently Asked Questions (FAQs)
Q1: Why are negative numbers confusing?
A1: Our intuition is largely shaped by our experience with positive numbers. The reversal of the comparison rule for negative numbers can feel counterintuitive at first. However, with practice and visualization using the number line, this confusion can be easily overcome.
Q2: Is there a trick to quickly compare negative numbers?
A2: Imagine the number line. For negative numbers, the number further to the left is smaller. You can also think of it in terms of debt: a larger debt (more negative) is worse (smaller) than a smaller debt.
Q3: How do I explain this concept to a child?
A3: Use visual aids like a thermometer or a number line. Explain that numbers to the left of zero represent amounts below zero (like temperature below freezing) and that further to the left means a lower value. Use relatable examples such as owing money.
Q4: Can I use a calculator to compare negative fractions?
A4: Yes, a calculator can convert fractions to decimals, making the comparison easier. However, understanding the underlying principles is crucial for developing a strong mathematical foundation.
Conclusion: Mastering the Comparison of Negative Numbers
Comparing negative numbers might initially seem challenging, but with a clear understanding of the number line and the concept of magnitude, it becomes straightforward. Remember that for negative numbers, the number further to the left on the number line is the smaller number. By practicing with examples and visualizing the numbers on the number line, you can build your confidence and accurately compare any negative numbers. So, next time you encounter a comparison involving negative numbers, remember the number line – your trusty guide to navigating the world of negative values! The key takeaway is that -1/2 is indeed greater than -3/2 because it lies to the right of -3/2 on the number line. Mastering this concept forms a solid foundation for more advanced mathematical concepts.
Latest Posts
Latest Posts
-
Explain The Kinetic Molecular Theory
Sep 15, 2025
-
Rna Is Produced By Blank
Sep 15, 2025
-
Organic Chemistry Acids And Bases
Sep 15, 2025
-
How To Predict Chemical Reactions
Sep 15, 2025
-
1000 Cm How Many Meters
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Is -1/2 Smaller Than -3/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.