Is -3/10 A Rational Number
zacarellano
Sep 24, 2025 · 6 min read
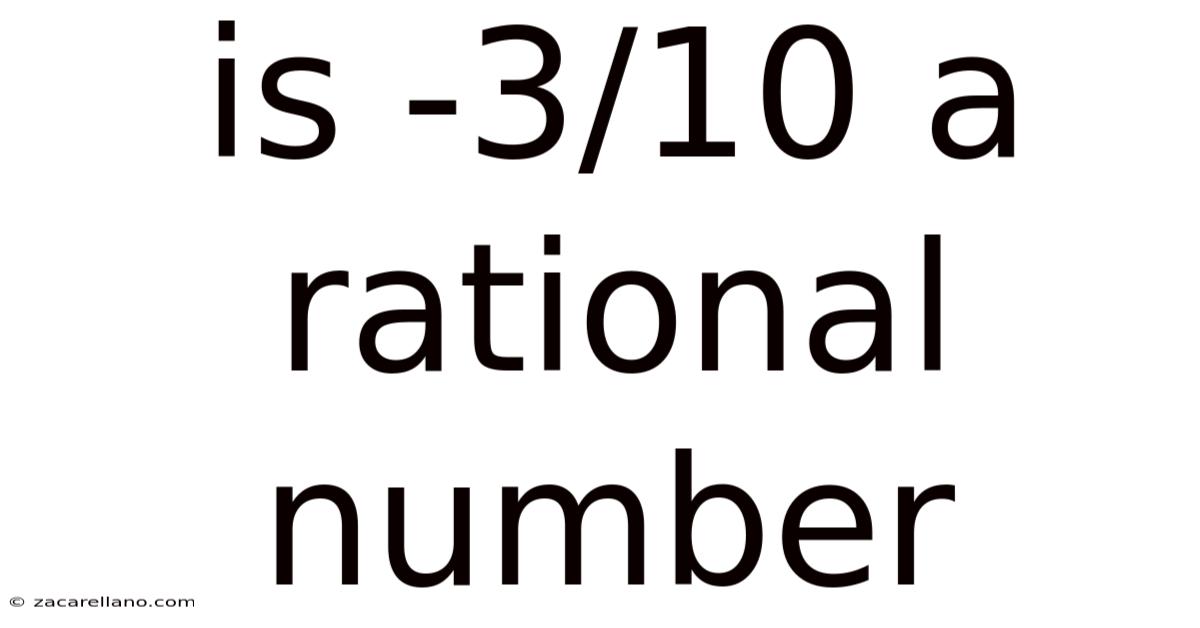
Table of Contents
Is -3/10 a Rational Number? A Deep Dive into Rational Numbers
Is -3/10 a rational number? The answer is a resounding yes, but understanding why requires a deeper exploration of what constitutes a rational number. This article will not only answer this specific question but also provide a comprehensive understanding of rational numbers, their properties, and how to identify them. We'll delve into the definition, explore examples, and address common misconceptions, ensuring a complete understanding of this fundamental mathematical concept. This detailed explanation will cover the theoretical underpinnings as well as practical applications, making it suitable for students and anyone interested in strengthening their mathematical foundation.
Understanding Rational Numbers: The Definition
A rational number is any number that can be expressed as the quotient or fraction p/q of two integers, a numerator 'p' and a non-zero denominator 'q'. This seemingly simple definition holds immense significance in mathematics. The key components are:
- Integers: Integers include all whole numbers (positive, negative, and zero). Examples: -3, 0, 5, 100, -2000.
- Fraction: The number is expressed as a fraction, a ratio of two integers.
- Non-zero denominator: The denominator (the bottom part of the fraction) cannot be zero. Division by zero is undefined in mathematics.
Why -3/10 is a Rational Number
Now, let's directly address the question: Is -3/10 a rational number? The answer is unequivocally yes. Let's examine why:
- -3 is an integer: -3 belongs to the set of integers.
- 10 is an integer: 10 is also an integer.
- The denominator is non-zero: The denominator, 10, is not zero.
Since -3/10 satisfies all the criteria for a rational number – it's a fraction of two integers with a non-zero denominator – it is classified as a rational number.
Examples of Rational Numbers
To further solidify the concept, let's explore a range of examples:
- Positive fractions: 1/2, 3/4, 5/7, 100/1.
- Negative fractions: -1/2, -3/4, -5/7, -100/1.
- Integers: Any integer can be expressed as a rational number by placing it over 1 (e.g., 5 = 5/1, -2 = -2/1).
- Terminating decimals: Decimals that end, such as 0.25 (which is 1/4), 0.75 (which is 3/4), or 0.5 (which is 1/2), are rational because they can be expressed as fractions.
- Repeating decimals: Decimals with a repeating pattern, like 0.333... (which is 1/3) or 0.142857142857... (which is 1/7), are also rational. While they appear infinite, the repeating pattern allows us to express them as fractions.
Examples of Numbers That Are NOT Rational Numbers (Irrational Numbers)
It's equally important to understand what isn't a rational number. These are called irrational numbers. Irrational numbers cannot be expressed as a fraction of two integers. They have decimal representations that are neither terminating nor repeating. Common examples include:
- π (pi): The ratio of a circle's circumference to its diameter, approximately 3.14159..., is an irrational number. Its decimal representation continues infinitely without a repeating pattern.
- √2 (the square root of 2): This number, approximately 1.414..., cannot be expressed as a fraction of two integers.
- e (Euler's number): The base of natural logarithms, approximately 2.71828..., is another irrational number.
Representing Rational Numbers: Fractions and Decimals
Rational numbers can be represented in two primary ways:
- Fractions: This is the most direct representation, showing the numerator and denominator explicitly (e.g., -3/10).
- Decimals: By performing the division (numerator divided by denominator), we can express a rational number as a decimal. Rational numbers will always result in either a terminating decimal (e.g., 1/4 = 0.25) or a repeating decimal (e.g., 1/3 = 0.333...).
The Significance of Rational Numbers in Mathematics
Rational numbers form the foundation of many mathematical concepts and operations. They are crucial in:
- Arithmetic: Adding, subtracting, multiplying, and dividing rational numbers are fundamental arithmetic operations.
- Algebra: Solving equations and inequalities often involves manipulating rational numbers.
- Geometry: Many geometric calculations utilize rational numbers.
- Calculus: Rational numbers play a vital role in the development and application of calculus.
Practical Applications of Rational Numbers
Rational numbers are not just abstract mathematical concepts; they have countless practical applications in everyday life:
- Measurements: Expressing lengths, weights, volumes, and other measurements often involves fractions or decimals (which represent rational numbers).
- Finance: Dealing with money involves fractions (e.g., 1/4 of a dollar) and decimals (e.g., $2.50).
- Cooking: Recipes often involve fractions (e.g., 1/2 cup of sugar).
- Engineering: Precise calculations in engineering often rely on rational numbers.
Addressing Common Misconceptions
Several misconceptions surround rational numbers:
- Negative numbers are not rational: This is incorrect. Negative numbers can be expressed as a fraction with a negative numerator and a positive denominator (or vice versa). -3/10 is a perfect example.
- Only positive fractions are rational: This is also wrong. Negative fractions are equally rational.
- Decimals are never rational: This is false. Terminating and repeating decimals are rational numbers. Only non-terminating, non-repeating decimals are irrational.
Frequently Asked Questions (FAQ)
Q1: Can a rational number be expressed as a decimal that goes on forever?
A1: Yes, but if it goes on forever, it must have a repeating pattern. Non-repeating, infinite decimals are irrational.
Q2: Is 0 a rational number?
A2: Yes, 0 can be expressed as 0/1 (or 0/any non-zero integer).
Q3: How can I convert a repeating decimal to a fraction?
A3: This involves algebraic manipulation. It requires setting up an equation, multiplying by a power of 10 to shift the decimal, and subtracting the original equation to eliminate the repeating part. This process results in a fraction.
Q4: What is the difference between a rational and an irrational number?
A4: A rational number can be expressed as a fraction of two integers; an irrational number cannot. Rational numbers have decimal representations that are either terminating or repeating; irrational numbers have non-terminating, non-repeating decimal representations.
Conclusion: A Firm Grasp of Rational Numbers
In conclusion, -3/10 is definitively a rational number because it meets the criteria: it's a fraction of two integers (-3 and 10) with a non-zero denominator. Understanding rational numbers is crucial for building a strong foundation in mathematics. This article aimed to provide a thorough and accessible explanation of this important concept, dispelling common misconceptions and showcasing the wide range of applications of rational numbers in various fields. By grasping the definition, exploring examples, and recognizing the distinction between rational and irrational numbers, you'll be well-equipped to tackle more advanced mathematical concepts with confidence. Remember, the seemingly simple concept of a rational number underlies much of the mathematical world around us.
Latest Posts
Latest Posts
-
External And Internal Character Traits
Sep 24, 2025
-
Intermolecular Forces Of Diethyl Ether
Sep 24, 2025
-
Define Zero Pairs In Math
Sep 24, 2025
-
Circle In A Triangle Symbol
Sep 24, 2025
-
Calculate The Heat Of Formation
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Is -3/10 A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.