Is -3/4 Or -11/12 Greater
zacarellano
Sep 13, 2025 · 5 min read
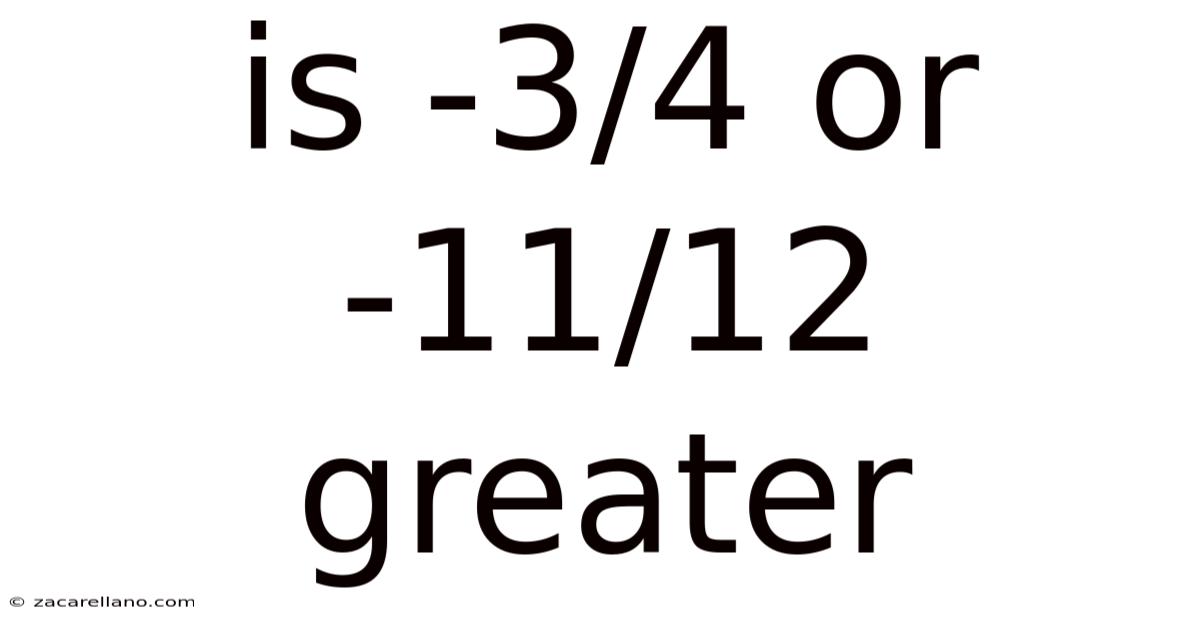
Table of Contents
Is -3/4 or -11/12 Greater? Understanding Negative Fractions
This article will delve into the comparison of two negative fractions, -3/4 and -11/12, providing a clear and comprehensive understanding of how to determine which is greater. We'll explore various methods, including visualizing on a number line, converting to decimals, finding a common denominator, and even applying the principles of absolute value. By the end, you'll not only know the answer but also possess a deeper understanding of comparing negative fractions, a crucial skill in mathematics.
Introduction: Navigating the World of Negative Fractions
Negative fractions represent values less than zero. Understanding their magnitude and comparing them requires a slightly different approach than comparing positive fractions. Many find this concept challenging, but with a structured approach, it becomes straightforward. This article aims to clarify the process of comparing negative fractions like -3/4 and -11/12, equipping you with the tools to tackle similar problems confidently. We'll examine several methods to solidify your understanding.
Method 1: Visualizing on a Number Line
A number line provides a visual representation of numbers. Placing -3/4 and -11/12 on a number line helps intuitively grasp which fraction is greater. Remember, on a number line, numbers increase as you move to the right and decrease as you move to the left. Zero is the central point.
Imagine a number line with 0 at the center. Now, consider the fractions. -3/4 is three-quarters of the way to -1 from 0. -11/12 is eleven-twelfths of the way to -1 from 0. Since -11/12 is closer to -1 than -3/4 is, it represents a smaller value. Therefore, -3/4 is greater than -11/12.
Method 2: Converting to Decimals
Converting fractions to decimals provides another way to compare them. To convert a fraction to a decimal, simply divide the numerator by the denominator.
- -3/4 = -0.75
- -11/12 ≈ -0.9167
Comparing the decimal values, -0.75 is greater than -0.9167. Therefore, again, -3/4 is greater than -11/12. This method is particularly useful when dealing with more complex fractions.
Method 3: Finding a Common Denominator
This is a fundamental method for comparing fractions. To compare -3/4 and -11/12, we find a common denominator, which is 12 in this case.
- -3/4 can be rewritten as -9/12 (multiply both numerator and denominator by 3).
Now, we compare -9/12 and -11/12. Since -9 is greater than -11, -9/12 (-3/4) is greater than -11/12. This method clearly illustrates the comparative values without the need for decimal conversions.
Method 4: Understanding Absolute Value and its Implications
The absolute value of a number is its distance from zero, regardless of its sign. While absolute value doesn't directly tell us which negative fraction is greater, it helps us understand their magnitudes.
- |-3/4| = 3/4 = 0.75
- |-11/12| = 11/12 ≈ 0.9167
The absolute values show that -11/12 is further from zero than -3/4. However, because we are dealing with negative numbers, the further a negative number is from zero, the smaller its value. Therefore, -3/4 is greater than -11/12. Understanding absolute value provides a valuable context for interpreting the comparison.
Further Exploration: Extending the Concept
The principles discussed here apply to comparing any two negative fractions. Let's consider a slightly more complex example: comparing -5/6 and -7/8.
-
Common Denominator: The least common denominator of 6 and 8 is 24.
- -5/6 = -20/24
- -7/8 = -21/24
-
Comparison: Since -20 > -21, -5/6 is greater than -7/8.
-
Decimal Conversion:
- -5/6 ≈ -0.8333
- -7/8 = -0.875
Again, confirming that -5/6 is greater.
Frequently Asked Questions (FAQ)
Q: Why is a smaller negative number greater than a larger negative number?
A: This is a common point of confusion. On the number line, numbers increase as you move to the right. Negative numbers are to the left of zero. Therefore, a number closer to zero (less negative) is greater than a number further from zero (more negative).
Q: Can I always use the common denominator method?
A: Yes, the common denominator method is a reliable way to compare any two fractions, regardless of their signs. It provides a direct and unambiguous comparison.
Q: Is there a quick way to compare negative fractions without calculations?
A: While not always precise for close values, a quick mental estimation can sometimes suffice. If the denominators are reasonably similar, you can often visually compare the numerators after quickly converting them to approximately the same denominator.
Q: What if the fractions have different signs, one positive and one negative?
A: In that case, the positive fraction will always be greater than the negative fraction.
Conclusion: Mastering Negative Fraction Comparison
Comparing negative fractions requires a clear understanding of the number line and the principles of magnitude. Using methods such as visualizing on a number line, converting to decimals, finding a common denominator, and considering absolute value allows for a thorough and accurate comparison. Remember, the "larger" negative number is actually the smaller value. With practice, you'll confidently navigate the world of negative fractions and solve comparison problems efficiently. The key is to choose the method that best suits your understanding and the complexity of the fractions you are comparing. By mastering these techniques, you'll build a solid foundation in fractional arithmetic and improve your overall mathematical proficiency.
Latest Posts
Latest Posts
-
How To Multiply Rational Numbers
Sep 13, 2025
-
Sample Space Of Two Dice
Sep 13, 2025
-
How To Find Leading Coefficient
Sep 13, 2025
-
Ap Physics 1 Sample Test
Sep 13, 2025
-
Is 1000 Ml 1 Liter
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Is -3/4 Or -11/12 Greater . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.