Is 3/5 Bigger Than 2/3
zacarellano
Sep 23, 2025 · 6 min read
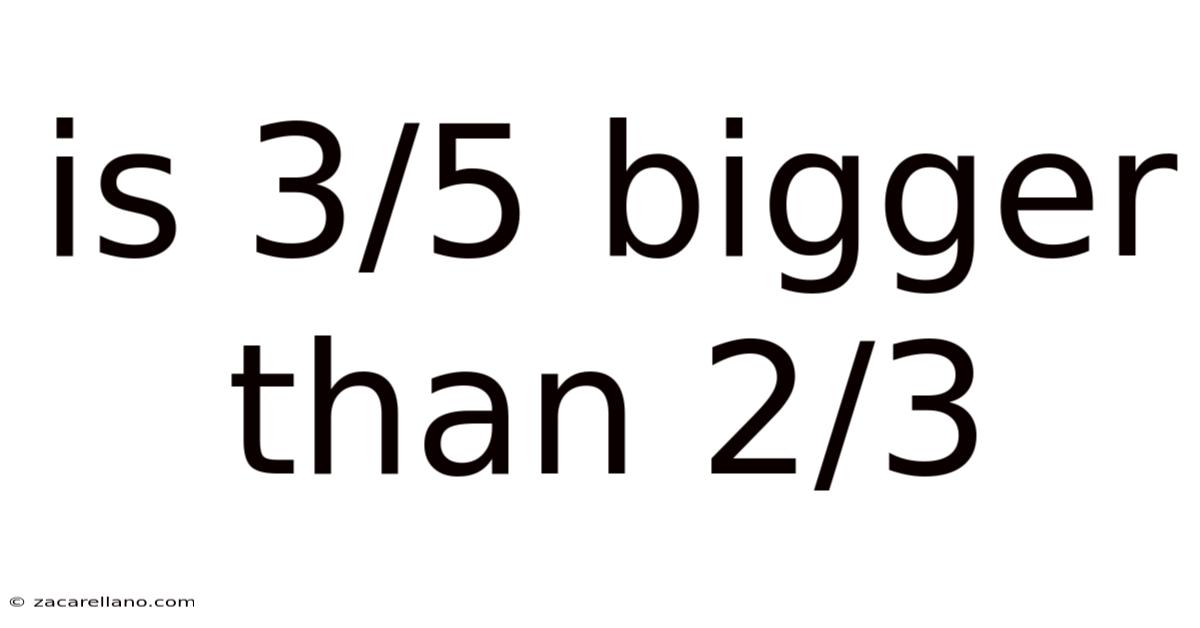
Table of Contents
Is 3/5 Bigger Than 2/3? A Deep Dive into Fraction Comparison
Determining whether 3/5 is bigger than 2/3 might seem like a simple task, especially for those comfortable with fractions. However, understanding the underlying principles behind fraction comparison is crucial for building a strong foundation in mathematics. This article will not only answer the question definitively but also explore various methods for comparing fractions, providing you with the tools to tackle similar problems with confidence. We'll delve into the practical application of these methods, address common misconceptions, and even explore the theoretical underpinnings of fraction comparison. By the end, you'll not only know if 3/5 is larger than 2/3, but you'll possess a deeper understanding of how fractions work.
Understanding Fractions: A Quick Refresher
Before we tackle the central question, let's refresh our understanding of what fractions represent. A fraction, such as 3/5, is a way of expressing a part of a whole. The number on top, the numerator (in this case, 3), represents the number of parts we have. The number on the bottom, the denominator (in this case, 5), represents the total number of equal parts the whole is divided into.
Therefore, 3/5 means we have 3 out of 5 equal parts of a whole. Similarly, 2/3 means we have 2 out of 3 equal parts of a whole. Comparing these fractions requires us to find a common ground – a way to assess which fraction represents a larger portion of the whole.
Method 1: Finding a Common Denominator
This is the most commonly taught method and arguably the most straightforward for comparing fractions. The process involves finding a common denominator, which is a number that both denominators can divide into evenly. Once we have a common denominator, we can directly compare the numerators.
Let's apply this to our problem: 3/5 and 2/3.
-
Find the least common multiple (LCM) of the denominators: The denominators are 5 and 3. The LCM of 5 and 3 is 15 (because 5 x 3 = 15, and 15 is the smallest number divisible by both 5 and 3).
-
Convert both fractions to equivalent fractions with the common denominator:
-
To convert 3/5 to an equivalent fraction with a denominator of 15, we multiply both the numerator and the denominator by 3: (3 x 3) / (5 x 3) = 9/15
-
To convert 2/3 to an equivalent fraction with a denominator of 15, we multiply both the numerator and the denominator by 5: (2 x 5) / (3 x 5) = 10/15
-
-
Compare the numerators: Now we have 9/15 and 10/15. Since 10 > 9, we can conclude that 10/15 is greater than 9/15.
-
Conclusion: Therefore, 2/3 (which is equal to 10/15) is bigger than 3/5 (which is equal to 9/15).
Method 2: Converting to Decimals
Another effective method for comparing fractions is to convert them into decimals. This method is particularly useful when dealing with fractions that don't easily share a common denominator.
-
Convert each fraction to a decimal:
-
To convert 3/5 to a decimal, we divide the numerator (3) by the denominator (5): 3 ÷ 5 = 0.6
-
To convert 2/3 to a decimal, we divide the numerator (2) by the denominator (3): 2 ÷ 3 ≈ 0.666... (This is a recurring decimal)
-
-
Compare the decimals: We now compare 0.6 and 0.666... Since 0.666... is greater than 0.6, we can conclude that 2/3 is bigger than 3/5.
Method 3: Visual Representation
While not as precise as the previous methods, visualizing fractions can be a helpful tool, especially for beginners. Imagine two identical bars or circles representing the whole. Divide one bar into 5 equal parts and shade 3 of them (representing 3/5). Divide the other bar into 3 equal parts and shade 2 of them (representing 2/3). By visually comparing the shaded areas, you can get a sense of which fraction is larger. While this method might not be precise for very close fractions, it offers a valuable intuitive understanding.
Addressing Common Misconceptions
A common misconception is to simply compare the numerators and denominators directly. It is incorrect to assume that because 3 (numerator of 3/5) is greater than 2 (numerator of 2/3), that 3/5 is automatically bigger than 2/3. The denominator plays a crucial role in determining the overall value of the fraction.
Another misconception arises when working with recurring decimals. Remember that even though 0.666… seems close to 0.7, it's still less than 0.7. It's important to understand the concept of infinity and how recurring decimals behave.
The Mathematical Underpinnings: Proportions and Ratios
At the heart of fraction comparison lies the concept of proportions and ratios. Fractions represent a ratio between two quantities. When comparing fractions, we are essentially comparing the relative sizes of these ratios. The methods we've explored – finding a common denominator and converting to decimals – are essentially different approaches to establishing a common reference point for comparison.
Practical Applications: Real-World Scenarios
Understanding fraction comparison is vital in various aspects of daily life. Consider the following scenarios:
- Cooking: Recipes often involve fractions. Determining whether you have enough of an ingredient requires comparing fractions.
- Construction: Precise measurements in construction projects often involve fractions of inches or centimeters.
- Finance: Understanding fractions is crucial for interpreting financial data like percentages and proportions of investments.
- Data Analysis: Interpreting data presented in fractional or percentage forms requires a solid grasp of fraction comparison.
Frequently Asked Questions (FAQ)
Q: Is there a quick way to compare fractions without using these methods?
A: For simple fractions, you might be able to estimate. However, using the methods described above provides accurate and reliable comparisons, especially for complex fractions.
Q: What if the fractions have very large denominators?
A: The methods described still apply, although finding the LCM might require more calculation. Using a calculator can simplify the process. Converting to decimals might be a more efficient approach in such cases.
Q: Can I use a calculator to compare fractions?
A: Yes, many calculators have fraction capabilities allowing for direct comparison or conversion to decimals.
Conclusion
We've definitively answered the initial question: 2/3 is bigger than 3/5. However, the true value of this exploration lies not just in the answer itself, but in the understanding of the different methods available for comparing fractions and the underlying mathematical concepts. Mastering fraction comparison is a foundational skill in mathematics with wide-ranging practical applications. By understanding the principles discussed here, you'll be well-equipped to tackle any fraction comparison problem with confidence and accuracy. Remember that practice is key! Try comparing different fractions using the methods described above to solidify your understanding and build your mathematical skills.
Latest Posts
Latest Posts
-
Work Done By Spring Equation
Sep 23, 2025
-
Absolute Max Vs Local Max
Sep 23, 2025
-
Difference Between Plants And Animals
Sep 23, 2025
-
Least Square Method Linear Algebra
Sep 23, 2025
-
Pressure To Flow Rate Equation
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Is 3/5 Bigger Than 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.