Is 5 More Than 25
zacarellano
Sep 22, 2025 · 7 min read
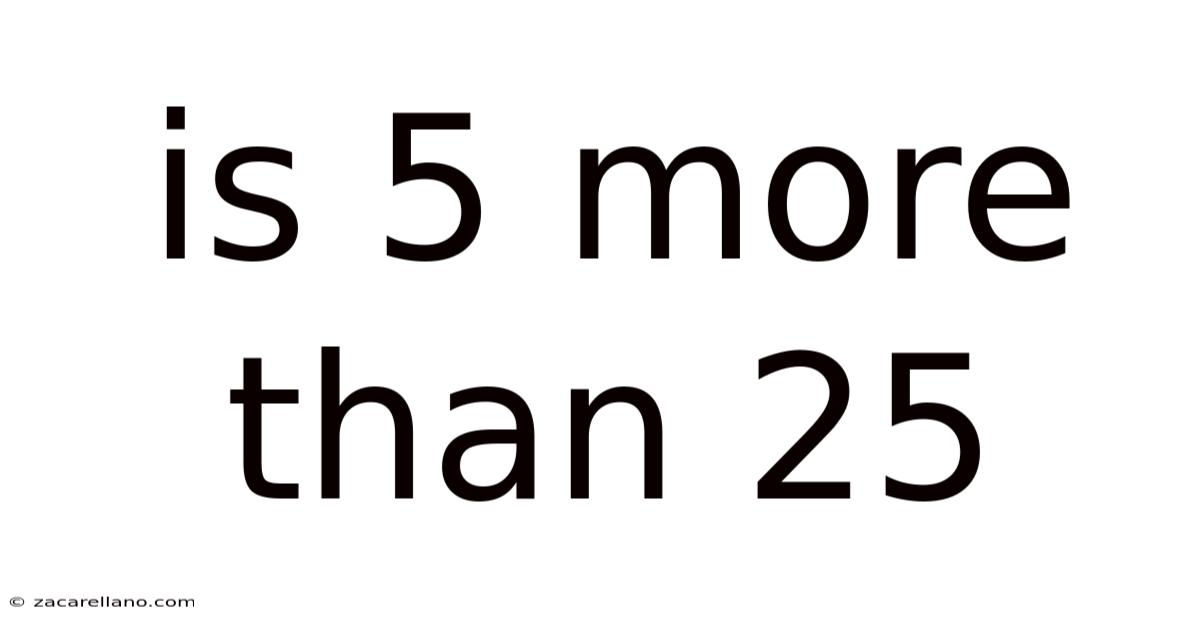
Table of Contents
Is 5 More Than 25? Understanding Number Relationships and Inequalities
This seemingly simple question, "Is 5 more than 25?", actually opens the door to a deeper understanding of number relationships, inequalities, and the fundamental concepts of mathematics. At first glance, the answer appears obvious: no. However, exploring this question allows us to delve into the precise language of mathematics and clarify common misconceptions about numerical comparisons. This article will explore this question in detail, examining the concepts of greater than, less than, and equality, and providing a comprehensive explanation suitable for learners of all levels.
Understanding Greater Than and Less Than
The core of this question lies in the understanding of the relational symbols ">" (greater than) and "<" (less than). These symbols are used to compare the magnitude of two numbers. A number is considered "greater than" another if it represents a larger quantity. Conversely, a number is "less than" another if it represents a smaller quantity.
Let's consider our initial question: Is 5 more than 25? Using the appropriate mathematical symbol, we can represent this as: 5 > 25. This statement is clearly false. The number 25 represents a significantly larger quantity than 5. The correct statement would be 5 < 25, indicating that 5 is less than 25.
Visualizing Number Relationships
Visual aids can significantly improve comprehension, especially when dealing with numerical comparisons. A number line is a helpful tool for visualizing the relative positions of numbers. On a number line, numbers increase from left to right. Placing 5 and 25 on a number line clearly shows that 5 lies to the left of 25, confirming that 5 is less than 25.
[Imagine a number line here with 5 and 25 clearly marked, illustrating 5 being to the left of 25]
Exploring the Concept of "More Than" in Different Contexts
While the direct mathematical answer to "Is 5 more than 25?" is a definitive "no," the phrase "more than" can have nuanced meanings in everyday language. It's crucial to distinguish between the mathematical interpretation and contextual interpretations.
For instance, if we are considering a situation involving debt, then it could be argued that someone who owes 5 dollars has "more than" someone who owes 25 dollars in the sense that their debt is less. This is not a mathematical comparison of the numbers themselves but a comparison of the negative values they represent in a specific context. In such a scenario, the statement "5 is more than 25" would refer to a lesser debt rather than a greater quantity.
Similarly, "more than" can be used in a qualitative, rather than quantitative way. For instance, one might say, "The simplicity of this task is more than that of the complex one". Here, "more than" refers to a higher degree of simplicity rather than a numerical comparison.
The Importance of Precision in Mathematical Language
The ambiguity that arises from the informal use of "more than" highlights the importance of precise language in mathematics. Mathematical symbols, such as > and <, remove any potential for misinterpretation. It's essential to use these symbols accurately when comparing numerical values to ensure clarity and prevent confusion. Using precise language is fundamental to accurate mathematical communication and problem-solving.
Expanding on Inequalities: Exploring Different Types of Inequalities
The comparison of 5 and 25 falls under the umbrella of inequalities. Inequalities are mathematical statements that compare two expressions using symbols such as > (greater than), < (less than), ≥ (greater than or equal to), and ≤ (less than or equal to).
-
Strict Inequalities: These inequalities use > and <, indicating that one value is strictly greater or less than another. The statement 5 < 25 is a strict inequality.
-
Non-Strict Inequalities: These inequalities use ≥ and ≤, indicating that one value is greater than or equal to, or less than or equal to, another. For example, x ≥ 10 means x can be 10 or any value greater than 10.
Understanding the different types of inequalities is crucial for solving mathematical problems and interpreting mathematical statements accurately.
Solving Inequalities: A Practical Example
Let's consider a simple inequality problem to further illustrate the concepts discussed. Suppose we have the inequality: x + 5 < 25. To solve for x, we need to isolate x on one side of the inequality. We can do this by subtracting 5 from both sides:
x + 5 - 5 < 25 - 5
This simplifies to:
x < 20
This solution means that any value of x less than 20 will satisfy the original inequality. For example, x could be 19, 10, 0, or -5.
Real-World Applications of Inequalities
Inequalities have wide-ranging applications in various fields, including:
-
Physics: Describing the range of possible values for physical quantities like speed, temperature, or pressure.
-
Engineering: Setting constraints and limits on design parameters.
-
Economics: Modeling economic relationships and predicting market trends.
-
Computer Science: Developing algorithms and controlling program flow.
-
Everyday Life: Making comparisons and decisions based on numerical data.
Number Systems and Comparisons: Beyond Whole Numbers
Our discussion so far has focused primarily on whole numbers. However, the concepts of greater than and less than apply to all number systems, including integers, rational numbers (fractions and decimals), irrational numbers (like π and √2), and real numbers. The relative magnitude of numbers remains consistent across different number systems. For instance, 0.5 is always less than 1, regardless of the number system in which it's expressed.
Addressing Common Misconceptions about Number Comparisons
Several common misconceptions can arise when comparing numbers:
-
Confusing magnitude with sign: A negative number is not inherently "smaller" than a positive number. For example, -5 is greater than -25 because it is closer to zero on the number line.
-
Misinterpreting inequalities: Failing to understand the difference between strict and non-strict inequalities can lead to incorrect solutions.
-
Ignoring context: Forgetting that "more than" can have different meanings in different situations can lead to misinterpretations.
Frequently Asked Questions (FAQ)
Q1: Is 5 ever more than 25?
A1: In the strict mathematical sense of numerical comparison, 5 is never more than 25. However, as discussed earlier, the phrase "more than" can have contextual meanings that might deviate from the pure mathematical interpretation.
Q2: How can I improve my understanding of inequalities?
A2: Practice solving inequality problems is key. Start with simple inequalities and gradually increase the complexity. Visual aids, such as number lines, can also be very helpful. Regular review of the concepts and definitions will further solidify your understanding.
Q3: What are some examples of inequalities in real life?
A3: Speed limits (your speed must be less than or equal to the posted limit), temperature ranges (the temperature should be between a certain minimum and maximum), budget constraints (your spending must be less than or equal to your available funds).
Q4: Can you provide another example of solving an inequality?
A4: Let’s solve 3x - 7 > 14. First, add 7 to both sides: 3x > 21. Then, divide both sides by 3: x > 7. This means any value greater than 7 satisfies the inequality.
Conclusion
While the straightforward answer to "Is 5 more than 25?" is a resounding "no," exploring this seemingly simple question has provided a valuable opportunity to delve into the fundamental concepts of number relationships, inequalities, and mathematical precision. Understanding the nuances of mathematical language, including the precise meaning of "greater than" and "less than," is crucial for accurate mathematical communication and problem-solving. This exploration underscores the importance of context, precision, and the application of these concepts in various aspects of life beyond simply comparing numbers. By understanding inequalities and their different forms, we equip ourselves with a fundamental tool for analyzing and interpreting numerical data across numerous fields. The journey from a simple question to a comprehensive understanding of inequalities highlights the depth and richness inherent in even the most basic mathematical concepts.
Latest Posts
Latest Posts
-
Which Best Describes Byzantine Culture
Sep 22, 2025
-
Convert 150 Degrees To Radians
Sep 22, 2025
-
Mixed Numerals And Improper Fractions
Sep 22, 2025
-
4th Grade Sicence Test Mock
Sep 22, 2025
-
Random Sample Ap Gov Definition
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Is 5 More Than 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.